19 września 2009
Tesseract (od starożytnego greckiego τέσσερες ἀκτῖνες - cztery promienie) to czterowymiarowy hipersześcian - odpowiednik sześcianu w przestrzeni czterowymiarowej.
Obraz jest rzutem (perspektywą) czterowymiarowego sześcianu na przestrzeń trójwymiarową.
Według Oxford Dictionary słowo „tesseract” zostało wymyślone i użyte w 1888 roku przez Charlesa Howarda Hintona (1853–1907) w jego książce A New Age of Thought. Później niektórzy nazywali tę samą figurę „tetrakostką”.
Geometria
Zwykły tesserakt w czterowymiarowej przestrzeni euklidesowej definiuje się jako wypukłą powłokę punktów (±1, ±1, ±1, ±1). Innymi słowy, można go przedstawić jako następujący zbiór:
Tesserakt ograniczony jest ośmioma hiperpłaszczyznami, których przecięcie z samym tesseraktem wyznacza jego trójwymiarowe ściany (które są zwykłymi sześcianami). Każda para nierównoległych ścian 3D przecina się, tworząc ściany 2D (kwadraty) i tak dalej. Wreszcie tesserakt ma 8 ścian 3D, 24 ściany 2D, 32 krawędzie i 16 wierzchołków.
Popularny opis
Spróbujmy sobie wyobrazić, jak będzie wyglądał hipersześcian, nie wychodząc z trójwymiarowej przestrzeni.
W jednowymiarowej „przestrzeni” – na prostej – wybieramy odcinek AB o długości L. Na dwuwymiarowej płaszczyźnie w odległości L od AB rysujemy równoległy do niego odcinek DC i łączymy ich końce. Rezultatem jest kwadrat ABCD. Powtarzając tę operację na płaszczyźnie, otrzymujemy trójwymiarowy sześcian ABCDEFG. A przesuwając sześcian w czwartym wymiarze (prostopadle do pierwszych trzech) o odległość L, otrzymujemy hipersześcian ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Construction_tesseract.PNG
Jednowymiarowy odcinek AB służy jako bok dwuwymiarowego kwadratu ABCD, kwadrat - jako bok sześcianu ABCDEFG, który z kolei będzie bokiem czterowymiarowego hipersześcianu. Odcinek linii prostej ma dwa punkty graniczne, kwadrat ma cztery wierzchołki, a sześcian ma osiem. W czterowymiarowym hipersześcianie będzie zatem 16 wierzchołków: 8 wierzchołków pierwotnego sześcianu i 8 wierzchołków przesuniętego w czwartym wymiarze. Ma 32 krawędzie - 12 wyznacza początkowe i końcowe położenie pierwotnego sześcianu, a kolejnych 8 krawędzi „rysuje” jego osiem wierzchołków, które przesunęły się do czwartego wymiaru. To samo rozumowanie można przeprowadzić w przypadku ścian hipersześcianu. W przestrzeni dwuwymiarowej jest tylko jedna (sam kwadrat), sześcian ma ich 6 (dwie ściany z przesuniętego kwadratu i kolejne cztery opisujące jego boki). Czterowymiarowy hipersześcian ma 24 kwadratowe ściany – 12 kwadratów pierwotnego sześcianu w dwóch pozycjach i 12 kwadratów z jego dwunastu krawędzi.
W podobny sposób możemy kontynuować nasze rozumowanie dla hipersześcianów o większej liczbie wymiarów, ale o wiele ciekawiej jest zobaczyć, jak czterowymiarowy hipersześcian będzie wyglądał dla nas, mieszkańców przestrzeni trójwymiarowej. W tym celu użyjemy znanej już metody analogii.
Rozpakowywanie Tesseractu
Weźmy sześcian z drutu ABCDEFG i spójrzmy na niego jednym okiem od strony krawędzi. Zobaczymy i potrafimy narysować na płaszczyźnie dwa kwadraty (jej bliższą i dalszą krawędź), połączone czterema liniami - krawędziami bocznymi. Podobnie czterowymiarowy hipersześcian w trójwymiarowej przestrzeni będzie wyglądał jak dwa sześcienne „pudełka” włożone w siebie i połączone ośmioma krawędziami. W tym przypadku same „pudełka” – trójwymiarowe twarze – zostaną zrzutowane na „naszą” przestrzeń, a łączące je linie rozciągną się w czwartym wymiarze. Możesz także spróbować wyobrazić sobie sześcian nie w rzucie, ale w obrazie przestrzennym.
Tak jak trójwymiarowy sześcian tworzy się z kwadratu przesuniętego o długość jego ściany, tak sześcian przesunięty do czwartego wymiaru utworzy hipersześcian. Ogranicza ją osiem kostek, które z perspektywy czasu będą wyglądać jak jakaś dość złożona figura. Linią ciągłą rysujemy część, która pozostała w „naszej” przestrzeni, a linią przerywaną część, która weszła w nadprzestrzeń. Sam czterowymiarowy hipersześcian składa się z nieskończonej liczby sześcianów, tak jak trójwymiarowy sześcian można „pociąć” na nieskończoną liczbę płaskich kwadratów.
Wycinając sześć ścian trójwymiarowego sześcianu, można go rozłożyć na płaską figurę – rozwinięcie. Będzie miał kwadrat po obu stronach oryginalnej twarzy, plus jeszcze jeden - twarz naprzeciwko. A trójwymiarowy rozwój czterowymiarowego hipersześcianu będzie się składał z oryginalnej kostki, sześciu kostek „wyrastających” z niej oraz jeszcze jednej - ostatecznej „hiperpowierzchni”.
Właściwości tesseraktu stanowią kontynuację właściwości figur geometrycznych o niższym wymiarze w przestrzeni czterowymiarowej.
Projekcje
Do przestrzeni dwuwymiarowej
Strukturę tę trudno sobie wyobrazić, ale możliwe jest rzutowanie tesseraktu na przestrzenie dwuwymiarowe lub trójwymiarowe. Ponadto rzutowanie na płaszczyznę ułatwia zrozumienie położenia wierzchołków hipersześcianu. W ten sposób można uzyskać obrazy, które nie odzwierciedlają już relacji przestrzennych w obrębie tesseraktu, ale ilustrują strukturę połączeń wierzchołków, jak w poniższych przykładach:
Do trójwymiarowej przestrzeni
Rzut tesseraktu na przestrzeń trójwymiarową przedstawia dwa zagnieżdżone trójwymiarowe sześciany, których odpowiadające wierzchołki są połączone segmentami. Sześcian wewnętrzny i zewnętrzny mają różne rozmiary w przestrzeni trójwymiarowej, ale w przestrzeni czterowymiarowej są równymi sześcianami. Aby zrozumieć równość wszystkich kostek tesseraktu, stworzono obrotowy model tesseraktu.
Sześć ściętych piramid wzdłuż krawędzi tesseraktu to obrazy równych sześciu sześcianów.
Para stereo
Para stereo tesseraktu jest przedstawiona jako dwie projekcje na trójwymiarową przestrzeń. Ten obraz tesseraktu został zaprojektowany tak, aby przedstawiać głębię jako czwarty wymiar. Para stereo jest oglądana w taki sposób, że każde oko widzi tylko jeden z tych obrazów, pojawia się obraz stereoskopowy, który odtwarza głębię tesseraktu.
Rozpakowywanie Tesseractu
Powierzchnię tesseraktu można rozłożyć na osiem sześcianów (podobnie jak powierzchnię sześcianu można rozłożyć na sześć kwadratów). Istnieje 261 różnych wzorów tesseraktu. Rozwinięcie tesseraktu można obliczyć, wykreślając połączone kąty na wykresie.
Tesserakt w sztuce
W „New Abbott Plain” Edwiny A. hipersześcian pełni rolę narratora.
W jednym z odcinków Przygód Jimmy'ego Neutrona: „Boy Genius” Jimmy wymyśla czterowymiarowy hipersześcian identyczny z składanym pudełkiem z powieści Heinleina Glory Road z 1963 roku.
Robert E. Heinlein wspomniał o hipersześcianach w co najmniej trzech opowiadaniach science fiction. W Domu czterech wymiarów (Dom, który zbudował turkus) (1940) opisał dom zbudowany na wzór rozpakowanego tesseraktu.
Powieść Heinleina Glory Road opisuje naczynia o dużych rozmiarach, które były większe w środku niż na zewnątrz.
Opowiadanie Henry'ego Kuttnera „Mimsy Were the Borogoves” opisuje edukacyjną zabawkę dla dzieci z odległej przyszłości, przypominającą budową tesserakt.
W powieści Alexa Garlanda (1999) termin „tesserakt” jest używany raczej do trójwymiarowego rozkładania czterowymiarowego hipersześcianu niż do samego hipersześcianu. Jest to metafora mająca pokazać, że system poznawczy musi być szerszy niż to, co poznawalne.
Fabuła Cube 2: Hypercube koncentruje się na ośmiu nieznajomych uwięzionych w „hipersześcianie”, czyli sieci połączonych kostek.
Serial telewizyjny Andromeda wykorzystuje generatory tesseraktu jako narzędzie fabularne. Ich głównym zadaniem jest manipulowanie przestrzenią i czasem.
Obraz „Ukrzyżowanie” (Corpus Hypercubus) Salvadora Dali (1954)
Komiks Nextwave przedstawia pojazd składający się z 5 stref tesseraktu.
Na płycie Voivod Nothingface jedna z kompozycji nosi tytuł „In my hypercube”.
W powieści Anthony'ego Pearce'a Route Cube jeden z orbitujących księżyców Międzynarodowego Stowarzyszenia Rozwoju nazywany jest tesseraktem, który został skompresowany w trzech wymiarach.
W serialu „Black Hole School” w trzecim sezonie znajduje się odcinek „Tesseract”. Lucas naciska tajny przycisk i szkoła zaczyna nabierać kształtu niczym matematyczny tesserakt.
Termin „tesserakt” i jego pochodny termin „tesserat” można znaleźć w opowiadaniu „Zmarszczka czasu” Madeleine L’Engle.
Hypersześcian i bryły platońskie
Modeluj dwudziestościan ścięty („piłka nożna”) w układzie „Wektor”.
w którym każdy pięciokąt jest ograniczony sześciokątami
Ścięty dwudziestościan można uzyskać poprzez odcięcie 12 wierzchołków, aby utworzyć ściany w postaci pięciokątów foremnych. W tym przypadku liczba wierzchołków nowego wielościanu wzrasta 5-krotnie (12×5=60), 20 ścian trójkątnych zamienia się w sześciokąty foremne (w sumie twarze stają się 20+12=32), A liczba krawędzi wzrasta do 30+12×5=90.







Etapy konstruowania dwudziestościanu ściętego w systemie Vector
Figury w przestrzeni 4-wymiarowej.
 --à
--à

 --à
?
--à
?
Na przykład biorąc pod uwagę sześcian i hipersześcian. Hipersześcian ma 24 ściany. Oznacza to, że 4-wymiarowy ośmiościan będzie miał 24 wierzchołki. Chociaż nie, hipersześcian ma 8 ścian sześcianów - każda ma środek w wierzchołku. Oznacza to, że 4-wymiarowy ośmiościan będzie miał 8 wierzchołków, co jest jeszcze lżejsze.


4-wymiarowy ośmiościan. Składa się z ośmiu równobocznych i równych czworościanów,
połączone czterema w każdym wierzchołku.






Ryż. Próba symulacji
hipersfera-hipersfera w układzie Vector
Twarze przód - tył - kulki bez zniekształceń. Kolejnych sześć kulek można zdefiniować za pomocą elipsoid lub powierzchni kwadratowych (poprzez 4 linie konturowe jako generatory) lub poprzez ściany (po raz pierwszy zdefiniowane za pomocą generatorów).


Więcej technik „budowania” hipersfery
- ta sama „piłka nożna” w przestrzeni 4-wymiarowej
Załącznik 2
Dla wielościanów wypukłych istnieje własność, która wiąże liczbę ich wierzchołków, krawędzi i ścian, udowodniona w 1752 roku przez Leonharda Eulera i zwana twierdzeniem Eulera.
Przed jego sformułowaniem rozważmy znane nam wielościany i wypełnij poniższą tabelę, w której B jest liczbą wierzchołków, P - krawędziami, a G - ścianami danego wielościanu:
|
Nazwa wielościanu |
|||
|
Trójkątna piramida |
|||
|
Piramida czworokątna |
|||
|
Trójkątny pryzmat |
|||
|
Pryzmat czworokątny |
|||
|
N-piramida węglowa |
N+1 |
2N |
N+1 |
|
N-pryzmat węglowy |
2N |
3N |
n+2 |
|
N-węgiel okrojony piramida |
2N |
3N |
n+2 |
Z tej tabeli od razu widać, że dla wszystkich wybranych wielościanów obowiązuje równość B - P + G = 2. Okazuje się, że ta równość obowiązuje nie tylko dla tych wielościanów, ale także dla dowolnego wielościanu wypukłego.
Twierdzenie Eulera. Dla każdego wielościanu wypukłego zachodzi równość
B - P + G = 2,
gdzie B to liczba wierzchołków, P to liczba krawędzi, a G to liczba ścian danego wielościanu.
Dowód. Aby udowodnić tę równość, wyobraźmy sobie powierzchnię tego wielościanu wykonaną z elastycznego materiału. Usuńmy (wytnijmy) jedną z jego ścian, a pozostałą powierzchnię rozciągnijmy na płaszczyznę. Otrzymujemy wielokąt (utworzony przez krawędzie usuniętej ściany wielościanu), podzielony na mniejsze wielokąty (utworzone przez pozostałe ściany wielościanu).
Należy pamiętać, że boki wielokątów można deformować, powiększać, zmniejszać, a nawet zakrzywiać, o ile po bokach nie ma przerw. Liczba wierzchołków, krawędzi i ścian nie ulegnie zmianie.
Udowodnimy, że powstały podział wielokąta na mniejsze wielokąty spełnia równość
(*)B - P + G " = 1,
gdzie B jest całkowitą liczbą wierzchołków, P jest całkowitą liczbą krawędzi, a Г " jest liczbą wielokątów zawartych w przegrodzie. Jasne jest, że Г " = Г - 1, gdzie Г jest liczbą ścian danego wielościan.
Udowodnijmy, że równość (*) nie zmienia się, jeśli w jakimś wielokącie danego podziału poprowadzona zostanie przekątna (ryc. 5, a). Rzeczywiście, po narysowaniu takiej przekątnej, nowa przegroda będzie miała B wierzchołków, krawędzie P+1, a liczba wielokątów wzrośnie o jeden. Dlatego mamy
B - (P + 1) + (G "+1) = B - P + G " .

Korzystając z tej właściwości, rysujemy przekątne, które dzielą nadchodzące wielokąty na trójkąty, a dla powstałego podziału pokazujemy wykonalność równości (*) (ryc. 5, b). Aby to zrobić, będziemy kolejno usuwać zewnętrzne krawędzie, zmniejszając liczbę trójkątów. W takim przypadku możliwe są dwa przypadki:
a) aby usunąć trójkąt ABC w naszym przypadku konieczne jest usunięcie dwóch żeber AB I PNE.;
b) aby usunąć trójkątMKNw naszym przypadku konieczne jest usunięcie jednej krawędziMN.
W obu przypadkach równość (*) nie ulegnie zmianie. Przykładowo w pierwszym przypadku po usunięciu trójkąta graf będzie składał się z B – 1 wierzchołków, P – 2 krawędzi i G” – 1 wielokąta:
(B - 1) - (P + 2) + (G " – 1) = B - P + G ".
Rozważ sam drugi przypadek.
Zatem usunięcie jednego trójkąta nie zmienia równości (*). Kontynuując proces usuwania trójkątów, w końcu dotrzemy do podziału składającego się z pojedynczego trójkąta. Dla takiego podziału B = 3, P = 3, Г " = 1, a zatem B – Р + Г " = 1. Oznacza to, że równość (*) zachodzi także dla pierwotnego podziału, z którego ostatecznie otrzymujemy, że dla tego podziału wielokąta równość (*) jest prawdziwa. Zatem dla pierwotnego wielościanu wypukłego prawdziwa jest równość B - P + G = 2.
Przykład wielościanu, dla którego nie obowiązuje relacja Eulera, pokazano na rysunku 6. Wielościan ten ma 16 wierzchołków, 32 krawędzie i 16 ścian. Zatem dla tego wielościanu zachodzi równość B – P + G = 0.
Dodatek 3.
Film Cube 2: Hypercube to film science fiction będący kontynuacją filmu Cube.
Ośmioro nieznajomych budzi się w pokojach w kształcie sześcianu. Pokoje znajdują się wewnątrz czterowymiarowego hipersześcianu. Pokoje nieustannie przechodzą przez „teleportację kwantową”, a jeśli wejdziesz do następnego pokoju, jest mało prawdopodobne, aby wrócić do poprzedniego. W hipersześcianie krzyżują się równoległe światy, w niektórych pomieszczeniach czas płynie inaczej, a niektóre pomieszczenia to śmiertelne pułapki.
Fabuła filmu w dużej mierze powtarza historię z pierwszej części, co znajduje odzwierciedlenie także w wizerunkach niektórych bohaterów. W pomieszczeniach hipersześcianu ginie laureat Nagrody Nobla Rosenzweig, który obliczył dokładny czas zniszczenia hipersześcianu..
Krytyka
O ile w pierwszej części uwięzieni w labiryncie ludzie próbowali sobie pomagać, o tyle w tym filmie każdy walczy o siebie. Jest mnóstwo niepotrzebnych efektów specjalnych (tzw. pułapek), które w żaden logiczny sposób nie łączą tej części filmu z poprzednią. Czyli okazuje się, że film Kostka 2 to swego rodzaju labirynt przyszłości 2020-2030, a nie 2000. W pierwszej części teoretycznie każdy rodzaj pułapek może być stworzony przez człowieka. W drugiej części pułapkami tymi jest swego rodzaju program komputerowy, tzw. „Wirtualna Rzeczywistość”.
W geometrii hipersześcian- Ten N-wymiarowa analogia kwadratu ( N= 2) i sześcian ( N= 3). Jest to zamknięta wypukła figura składająca się z grup równoległych linii znajdujących się na przeciwległych krawędziach figury i połączonych ze sobą pod kątem prostym.
Liczba ta jest również znana jako tesserakt(tesserakt). Tesserakt ma się do sześcianu tak, jak sześcian do kwadratu. Bardziej formalnie tesserakt można opisać jako regularny wypukły czterowymiarowy wielościan (wielościan), którego granica składa się z ośmiu sześciennych komórek.
Według Oxford English Dictionary słowo „tesseract” zostało wymyślone w 1888 roku przez Charlesa Howarda Hintona i użyte w jego książce „A New Era of Thought”. Słowo to pochodzi od greckiego „τεσσερες ακτινες” („cztery promienie”) i ma postać czterech osi współrzędnych. Ponadto w niektórych źródłach nazywano tę samą liczbę tetrasześcian(tetrasześcian).
N-wymiarowy hipersześcian jest również nazywany n-sześcian.
Punkt jest hipersześcianem o wymiarze 0. Jeśli przesuniesz punkt o jednostkę długości, otrzymasz odcinek o jednostkowej długości - hipersześcian o wymiarze 1. Ponadto, jeśli przesuniesz odcinek o jednostkę długości w kierunku prostopadłym do kierunku odcinka otrzymujemy sześcian - hipersześcian o wymiarze 2. Przesuwając kwadrat o jednostkę długości w kierunku prostopadłym do płaszczyzny kwadratu, otrzymujemy sześcian - hipersześcian o wymiarze 3. Proces ten można uogólnić na dowolną liczbę wymiarów. Na przykład, jeśli przesuniesz sześcian o jedną jednostkę długości w czwartym wymiarze, otrzymasz tesserakt.
Rodzina hipersześcianów jest jednym z niewielu wielościanów foremnych, które można przedstawić w dowolnym wymiarze.
Elementy hipersześcianu
Wymiarowy hipersześcian N ma 2 N„boki” (jednowymiarowa linia ma 2 punkty, dwuwymiarowy kwadrat ma 4 boki, trójwymiarowy sześcian ma 6 ścian, czterowymiarowy tesserakt ma 8 komórek). Liczba wierzchołków (punktów) hipersześcianu wynosi 2 N(na przykład dla sześcianu - 2 3 wierzchołki).
Ilość M-wymiarowe hipersześciany na granicy N-sześcian równa się
Na przykład na granicy hipersześcianu znajduje się 8 sześcianów, 24 kwadraty, 32 krawędzie i 16 wierzchołków.
| n-sześcian | Nazwa | Wierzchołek (0-twarz) |
Krawędź (1-twarz) |
Krawędź (2-twarzy) |
Komórka (3 twarze) |
(4-twarzy) | (5 twarzy) | (6-stronny) | (7 twarzy) | (8 twarzy) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-kostka | Kropka | 1 | ||||||||
| 1-kostka | Odcinek | 2 | 1 | |||||||
| 2-kostka | Kwadrat | 4 | 4 | 1 | ||||||
| 3-kostka | Sześcian | 8 | 12 | 6 | 1 | |||||
| 4-kostka | Tesserakt | 16 | 32 | 24 | 8 | 1 | ||||
| 5 kostek | Penterakt | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6 kostek | Hexerakt | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7 kostek | Hepterakt | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8 kostek | Okterakt | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-sześcian | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Projekcja na płaszczyznę
Tworzenie hipersześcianu można przedstawić w następujący sposób:
- Dwa punkty A i B można połączyć w odcinek AB.
- Dwa równoległe odcinki AB i CD można połączyć tak, aby powstał kwadrat ABCD.
- Dwa równoległe kwadraty ABCD i EFGH można połączyć, tworząc sześcian ABCDEFGH.
- Dwa równoległe sześciany ABCDEFGH i IJKLMNOP można połączyć, tworząc hipersześcian ABCDEFGHIJKLMNOP.
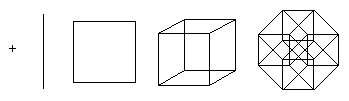
Ta ostatnia struktura nie jest łatwa do wizualizacji, ale możliwe jest zobrazowanie jej rzutu na przestrzeń dwuwymiarową lub trójwymiarową. Co więcej, rzuty na płaszczyznę dwuwymiarową mogą być bardziej przydatne, umożliwiając zmianę położenia rzutowanych wierzchołków. W tym przypadku możliwe jest uzyskanie obrazów, które nie odzwierciedlają już relacji przestrzennych elementów w obrębie tesseraktu, ale ilustrują strukturę połączeń wierzchołków, jak w przykładach poniżej.

Pierwsza ilustracja pokazuje, jak w zasadzie tesserakt powstaje poprzez połączenie dwóch sześcianów. Ten schemat jest podobny do schematu tworzenia sześcianu z dwóch kwadratów. Drugi diagram pokazuje, że wszystkie krawędzie tesseraktu mają tę samą długość. Schemat ten wymusza także szukanie połączonych ze sobą kostek. Na trzecim schemacie wierzchołki tesseraktu rozmieszczone są zgodnie z odległościami wzdłuż ścian względem punktu dolnego. Schemat ten jest interesujący, ponieważ jest stosowany jako podstawowy schemat topologii sieci łączących procesory podczas organizacji obliczeń równoległych: odległość między dowolnymi dwoma węzłami nie przekracza 4 długości krawędzi i istnieje wiele różnych ścieżek równoważenia obciążenia.
Hipersześcian w sztuce
Hipersześcian pojawia się w literaturze science fiction od 1940 roku, kiedy to Robert Heinlein w opowiadaniu „I zbudował krzywy dom” opisał dom zbudowany na kształt skanu tesseraktu. W opowieści Next ten dom zawala się, zamieniając się w czterowymiarowy tesserakt. Następnie hipersześcian pojawia się w wielu książkach i opowiadaniach.
Film Cube 2: Hypercube opowiada o ośmiu osobach uwięzionych w sieci hipersześcianów.
Obraz Salvadora Dali „Ukrzyżowanie (Corpus Hypercubus)”, 1954, przedstawia Jezusa ukrzyżowanego na skanie tesseraktu. Obraz ten można oglądać w Metropolitan Museum of Art w Nowym Jorku.
Wniosek
Hipersześcian to jeden z najprostszych obiektów czterowymiarowych, z którego widać złożoność i niezwykłość czwartego wymiaru. A to, co wydaje się niemożliwe w trzech wymiarach, jest możliwe w czterech, na przykład, niemożliwych figurach. Na przykład pręty niemożliwego trójkąta w czterech wymiarach zostaną połączone pod kątem prostym. I ta figura będzie tak wyglądać ze wszystkich punktów widzenia i nie będzie zniekształcona, w przeciwieństwie do realizacji niemożliwego trójkąta w przestrzeni trójwymiarowej (patrz.
Doktryna przestrzeni wielowymiarowych zaczęła pojawiać się w połowie XIX wieku w pracach G. Grassmanna, A. Cayleya, B. Riemanna, W. Clifforda, L. Schläfli i innych matematyków. Na początku XX wieku, wraz z pojawieniem się teorii względności A. Einsteina i idei G. Minkowskiego, w fizyce zaczęto stosować czterowymiarowy układ współrzędnych czasoprzestrzennych.
Następnie ideę przestrzeni czterowymiarowej zapożyczono od naukowców przez pisarzy science fiction. W swoich pracach opowiedzieli światu o niesamowitych cudach czwartego wymiaru. Bohaterowie swoich dzieł, wykorzystując właściwości czterowymiarowej przestrzeni, mogli zjeść zawartość jajka bez uszkodzenia skorupki i wypić napój bez otwierania nakrętki. Złodzieje usunęli skarb z sejfu przez czwarty wymiar. Ogniwa łańcuszka można łatwo rozłączyć, a węzeł na linie można rozwiązać bez dotykania jej końców. Chirurdzy przeprowadzali operacje narządów wewnętrznych, nie nacinając tkanki ciała pacjenta. Mistycy umieszczali dusze zmarłych w czwartym wymiarze. Dla zwykłego człowieka idea przestrzeni czterowymiarowej pozostała niezrozumiała i tajemnicza, a wielu ogólnie uważa przestrzeń czterowymiarową za wytwór wyobraźni naukowców i pisarzy science fiction, który nie ma nic wspólnego z rzeczywistością.
Problem percepcji
Tradycyjnie uważa się, że człowiek nie może postrzegać i wyobrażać sobie postaci czterowymiarowych, ponieważ jest istotą trójwymiarową. Osoba badana postrzega trójwymiarowe postacie za pomocą siatkówki, która jest dwuwymiarowa. Aby dostrzec postacie czterowymiarowe, potrzebna jest trójwymiarowa siatkówka, ale ludzie nie mają takiej zdolności.
Aby uzyskać jasny obraz figur czterowymiarowych, użyjemy analogii z przestrzeni niższych wymiarów w celu ekstrapolacji na figury o wyższych wymiarach, zastosujemy metodę modelowania i zastosujemy metody analizy systemów w celu poszukiwania wzorców między elementami cztero-wymiarowymi. figury wymiarowe. Proponowane modele muszą adekwatnie opisywać właściwości figur czterowymiarowych, nie być ze sobą sprzeczne i dawać wystarczające zrozumienie figury czterowymiarowej, a przede wszystkim jej kształtu geometrycznego. Ponieważ w literaturze nie ma systematycznego i wizualnego opisu figur czterowymiarowych, a jedynie ich nazwy wskazujące na pewne właściwości, proponujemy rozpocząć badanie figur czterowymiarowych od najprostszego - czterowymiarowego sześcianu, który nazywa się hipersześcian.
Definicja hipersześcianu
Hipersześcianjest regularnym wielokątem, którego komórka jest sześcianem.
Politop jest figurą czterowymiarową, której brzegi składają się z wielościanów. Analogiem komórki politopowej jest ściana wielościanu. Hipersześcian jest analogiem trójwymiarowego sześcianu.
Będziemy mieli pojęcie o hipersześcianie, jeśli znamy jego właściwości. Podmiot postrzega pewien przedmiot, przedstawiając go w postaci określonego modelu. Skorzystajmy z tej metody i przedstawmy ideę hipersześcianu w postaci różnych modeli.
Model analityczny
Przestrzeń jednowymiarową (prostą) będziemy rozpatrywać jako uporządkowany zbiór punktówM(X), Gdzie X– współrzędna dowolnego punktu na linii. Następnie określa się segment jednostkowy poprzez podanie dwóch punktów:A(0) i B(1).
Płaszczyznę (przestrzeń dwuwymiarową) można uznać za uporządkowany zbiór punktów M(X; y). Kwadrat jednostkowy zostanie całkowicie zdefiniowany przez jego cztery wierzchołki: A(0; 0), B(1; 0), C(1; 1), D(0; 1). Współrzędne wierzchołków kwadratu uzyskuje się dodając zero, a następnie jeden do współrzędnych odcinka.
Przestrzeń trójwymiarowa - uporządkowany zbiór punktów M(X; y; z). Aby zdefiniować trójwymiarową kostkę, potrzeba ośmiu punktów:
A(0; 0; 0), B(1; 0; 0), C(1; 1; 0), D(0; 1; 0),
mi(0; 0; 1), F(1; 0; 1), G(1; 1; 1), H(0; 1; 1).
Współrzędne sześcianu uzyskuje się ze współrzędnych kwadratu przez dodanie zera, a następnie jedynki.
Przestrzeń czterowymiarowa to uporządkowany zbiór punktów M(X; y; z; T). Aby zdefiniować hipersześcian, należy określić współrzędne jego szesnastu wierzchołków:
A(0; 0; 0; 0), B(1; 0; 0; 0), C(1; 1; 0; 0), D(0; 1; 0; 0),
mi(0; 0; 1; 0), F(1; 0; 1; 0), G(1; 1; 1; 0), H(0; 1; 1; 0),
K(0; 0; 0; 1), L(1; 0; 0; 1), M(1; 1; 0; 1), N(0; 1; 0; 1),
O(0; 0; 1; 1), P(1; 0; 1; 1), R(1; 1; 1; 1), S(0; 1; 1; 1).
Współrzędne hipersześcianu uzyskuje się ze współrzędnych trójwymiarowego sześcianu poprzez dodanie czwartej współrzędnej równej zeru, a następnie jedności.
Korzystając ze wzorów geometrii analitycznej dla czterowymiarowej przestrzeni euklidesowej, można otrzymać właściwości hipersześcianu.
Jako przykład rozważmy obliczenie długości głównej przekątnej hipersześcianu. Załóżmy, że musimy znaleźć odległość między punktami A(0, 0, 0, 0) i R(1, 1, 1, 1). W tym celu skorzystamy ze wzoru na odległość w czterowymiarowej przestrzeni euklidesowej.
W przestrzeni dwuwymiarowej (na płaszczyźnie) odległość między punktami A(X 1 , y 1) i B(X 2 , y 2) obliczone według wzoru
Wzór ten wynika z twierdzenia Pitagorasa.
Odpowiedni wzór na odległość między punktami A(X 1 , y 1 , z 1) i B(X 2 , y 2 , z 2) w przestrzeni trójwymiarowej ma postać
Oraz w przestrzeni jednowymiarowej (na prostej) pomiędzy punktami A( X 1) i B( X 2) możesz napisać odpowiedni wzór na odległość:
Podobnie odległość między punktami A(X 1 , y 1 , z 1 , T 1) i B(X 2 , y 2 , z 2 , T 2) w przestrzeni czterowymiarowej oblicza się według wzoru:
Dla proponowanego przykładu znajdujemy
Zatem hipersześcian istnieje analitycznie, a jego właściwości można opisać nie gorzej niż właściwości trójwymiarowego sześcianu.
Model dynamiczny
Model analityczny hipersześcianu jest bardzo abstrakcyjny, dlatego rozważmy inny model – dynamiczny.
Punkt (figura zerowymiarowa), poruszając się w jednym kierunku, generuje odcinek (figurę jednowymiarową). Odcinek poruszając się w kierunku prostopadłym do siebie tworzy kwadrat (figurę dwuwymiarową). Kwadrat poruszając się w kierunku prostopadłym do płaszczyzny kwadratu, tworzy sześcian (figurę trójwymiarową).
Sześcian poruszając się prostopadle do trójwymiarowej przestrzeni, w której pierwotnie się znajdował, generuje hipersześcian (figurę czterowymiarową).
Granica hipersześcianu jest trójwymiarowa, skończona i zamknięta. Składa się z trójwymiarowego sześcianu w położeniu początkowym, trójwymiarowego sześcianu w położeniu końcowym oraz sześciu sześcianów powstałych poprzez przesunięcie kwadratów pierwotnego sześcianu w kierunku czwartego wymiaru. Cała granica hipersześcianu składa się z 8 trójwymiarowych kostek (komórek).
Podczas poruszania się w położeniu początkowym sześcian miał 8 wierzchołków, a w położeniu końcowym również 8 wierzchołków. Zatem hipersześcian ma w sumie 16 wierzchołków.
Z każdego wierzchołka wychodzą cztery wzajemnie prostopadłe krawędzie. Hipersześcian ma łącznie 32 krawędzie, w położeniu początkowym miał 12 krawędzi, w położeniu końcowym również 12 krawędzi, a 8 krawędzi tworzyło wierzchołki sześcianu podczas poruszania się w czwartym wymiarze.
Zatem granica hipersześcianu składa się z 8 kostek, które składają się z 24 kwadratów. Mianowicie 6 kwadratów w pozycji początkowej, 6 w pozycji końcowej i 12 kwadratów utworzonych przez przesunięcie 12 krawędzi w kierunku czwartego wymiaru.
Model geometryczny
Dynamiczny model hipersześcianu może nie wydawać się wystarczająco jasny. Dlatego rozważ model geometryczny hipersześcianu. Jak uzyskać model geometryczny sześcianu 3D? Wykonujemy jego rozwinięcie i z rozwinięcia „sklejamy” model sześcianu. Rozwój trójwymiarowego sześcianu składa się z kwadratu, do którego boków przymocowany jest kwadrat plus kolejny kwadrat.  Obracamy sąsiednie kwadraty wokół boków kwadratu i łączymy ze sobą sąsiednie boki kwadratów. I zamykamy pozostałe cztery boki ostatnim kwadratem (ryc. 1).
Obracamy sąsiednie kwadraty wokół boków kwadratu i łączymy ze sobą sąsiednie boki kwadratów. I zamykamy pozostałe cztery boki ostatnim kwadratem (ryc. 1).
Rozważmy podobnie rozwój hipersześcianu. Jego rozwinięciem będzie trójwymiarowa figura składająca się z oryginalnej trójwymiarowej kostki, sześciu kostek sąsiadujących z każdą ścianą oryginalnej kostki i jeszcze jednej kostki. W sumie jest osiem trójwymiarowych kostek (ryc. 2). Aby otrzymać z tego opracowania czterowymiarową kostkę (hipersześcian), należy obrócić każdą z sąsiednich kostek o 90 stopni. Te sąsiednie kostki będą zlokalizowane w innej trójwymiarowej przestrzeni. Połącz ze sobą sąsiednie ściany (kwadraty) sześcianów. Umieść ósmą kostkę swoimi ścianami na pozostałym pustym miejscu. Otrzymujemy czterowymiarową figurę - hipersześcian, którego granicę stanowi osiem trójwymiarowych kostek.
Obraz hipersześcianu
 Powyżej pokazano jak „skleić” model hipersześcianu z trójwymiarowego skanu. Obrazy uzyskujemy za pomocą projekcji. Rzut centralny trójwymiarowego sześcianu (jego obraz na płaszczyźnie) wygląda następująco (ryc. 3). Wewnątrz kwadratu znajduje się kolejny kwadrat. Odpowiednie wierzchołki kwadratu są połączone odcinkami. Sąsiednie kwadraty są przedstawiane jako trapezy, chociaż w przestrzeni trójwymiarowej są kwadratami. Kwadraty wewnętrzne i zewnętrzne mają różne rozmiary, ale w prawdziwej trójwymiarowej przestrzeni są równymi kwadratami.
Powyżej pokazano jak „skleić” model hipersześcianu z trójwymiarowego skanu. Obrazy uzyskujemy za pomocą projekcji. Rzut centralny trójwymiarowego sześcianu (jego obraz na płaszczyźnie) wygląda następująco (ryc. 3). Wewnątrz kwadratu znajduje się kolejny kwadrat. Odpowiednie wierzchołki kwadratu są połączone odcinkami. Sąsiednie kwadraty są przedstawiane jako trapezy, chociaż w przestrzeni trójwymiarowej są kwadratami. Kwadraty wewnętrzne i zewnętrzne mają różne rozmiary, ale w prawdziwej trójwymiarowej przestrzeni są równymi kwadratami.
 Podobnie centralny rzut czterowymiarowego sześcianu na przestrzeń trójwymiarową będzie wyglądał następująco: wewnątrz jednego sześcianu znajduje się drugi sześcian. Odpowiednie wierzchołki sześcianów są połączone segmentami. Sześcian wewnętrzny i zewnętrzny mają różne rozmiary w przestrzeni trójwymiarowej, natomiast w przestrzeni czterowymiarowej są sześcianami równymi (ryc. 4).
Podobnie centralny rzut czterowymiarowego sześcianu na przestrzeń trójwymiarową będzie wyglądał następująco: wewnątrz jednego sześcianu znajduje się drugi sześcian. Odpowiednie wierzchołki sześcianów są połączone segmentami. Sześcian wewnętrzny i zewnętrzny mają różne rozmiary w przestrzeni trójwymiarowej, natomiast w przestrzeni czterowymiarowej są sześcianami równymi (ryc. 4).
Sześć ściętych piramid to obrazy równych sześciu komórek (sześcianów) czterowymiarowego sześcianu.
Ten trójwymiarowy rzut można narysować na płaszczyźnie i sprawdzić, czy właściwości hipersześcianu uzyskane za pomocą modelu dynamicznego są prawdziwe.
Hipersześcian ma 16 wierzchołków, 32 krawędzie, 24 ściany (kwadraty) i 8 komórek (sześciany). Z każdego wierzchołka wychodzą cztery wzajemnie prostopadłe krawędzie. Granica hipersześcianu jest trójwymiarową, zamkniętą wypukłą figurą, której objętość (objętość boczna hipersześcianu) jest równa ośmiu jednostkowym trójwymiarowym sześcianom. Wewnątrz tej figury znajduje się hipersześcian jednostkowy, którego hiperobjętość jest równa hiperobjętości hipersześcianu jednostkowego.
Wniosek
Celem tej pracy było wstępne wprowadzenie do przestrzeni czterowymiarowej. Dokonano tego na przykładzie najprostszej figury – hipersześcianu.
Świat czterowymiarowej przestrzeni jest niesamowity! W nim, wraz z podobnymi figurami w przestrzeni trójwymiarowej, znajdują się także figury, które nie mają analogii w przestrzeni trójwymiarowej.
Wiele zjawisk świata materialnego, makroświata i megaświata, pomimo ogromnych sukcesów w fizyce, chemii i astronomii, pozostało niewyjaśnionych.
Nie ma jednej teorii wyjaśniającej wszystkie siły natury. Nie ma zadowalającego modelu Wszechświata, który wyjaśniałby jego budowę i wykluczał paradoksy.
Poznając właściwości przestrzeni czterowymiarowej i zapożyczając pewne pomysły z geometrii czterowymiarowej, możliwe będzie nie tylko budowanie bardziej rygorystycznych teorii i modeli świata materialnego, ale także tworzenie narzędzi i systemów funkcjonujących zgodnie z prawami czterowymiarowego świata, wówczas możliwości człowieka będą jeszcze bardziej imponujące.
Bakaljar Maria
Badane są metody wprowadzania pojęcia czterowymiarowego sześcianu (tesserakt), jego struktura i niektóre właściwości.Zagadnienie, jakie trójwymiarowe obiekty powstają, gdy czterowymiarowy sześcian przecina się hiperpłaszczyznami równoległymi do jego trójwymiarowych ścian , a także hiperpłaszczyzny prostopadłe do jej głównej przekątnej. Rozważono aparaturę wielowymiarowej geometrii analitycznej wykorzystywaną do badań.
Pobierać:
Zapowiedź:
Wprowadzenie…………………………………………………………………………….2
Część główna…………………………………………………………..4
Wnioski……….. ……………………………………………………..12
Referencje………………………………………………………..13
Wstęp
Przestrzeń czterowymiarowa od dawna przyciąga uwagę zarówno zawodowych matematyków, jak i osób dalekich od studiowania tej nauki. Zainteresowanie czwartym wymiarem może wynikać z założenia, że nasz trójwymiarowy świat jest „zanurzony” w przestrzeni czterowymiarowej, tak jak płaszczyzna jest „zanurzana” w przestrzeni trójwymiarowej, a linia prosta „zanurza się” w przestrzeń trójwymiarową. płaszczyźnie, a punkt leży na linii prostej. Ponadto przestrzeń czterowymiarowa odgrywa ważną rolę we współczesnej teorii względności (tzw. czasoprzestrzeń lub przestrzeń Minkowskiego), a także może być traktowana jako przypadek szczególnywymiarowa przestrzeń euklidesowa (z).
Czterowymiarowa kostka (tesserakt) to obiekt w przestrzeni czterowymiarowej, który ma maksymalny możliwy wymiar (tak jak zwykła kostka jest obiektem w przestrzeni trójwymiarowej). Należy zauważyć, że ma to także bezpośrednie znaczenie, mianowicie może pojawiać się w problemach optymalizacyjnych programowania liniowego (jako obszar, w którym znajduje się minimum lub maksimum funkcji liniowej czterech zmiennych), a także jest wykorzystywane w mikroelektronice cyfrowej (gdy programowanie działania wyświetlacza zegarka elektronicznego). Ponadto sam proces studiowania czterowymiarowej kostki przyczynia się do rozwoju myślenia przestrzennego i wyobraźni.
W związku z tym badanie struktury i specyficznych właściwości czterowymiarowego sześcianu jest dość istotne. Warto zauważyć, że pod względem struktury czterowymiarowy sześcian został dość dobrze zbadany. Dużo ciekawszy jest charakter jej przekrojów różnymi hiperpłaszczyznami. Zatem głównym celem tej pracy jest zbadanie struktury tesseraktu, a także wyjaśnienie pytania, jakie trójwymiarowe obiekty zostaną uzyskane, jeśli czterowymiarowy sześcian zostanie przecięty hiperpłaszczyznami równoległymi do jednej z jego trójwymiarowych powierzchnie wymiarowe lub hiperpłaszczyznami prostopadłymi do jego głównej przekątnej. Hiperpłaszczyzna w przestrzeni czterowymiarowej będzie nazywana podprzestrzenią trójwymiarową. Można powiedzieć, że linia prosta na płaszczyźnie jest hiperpłaszczyzną jednowymiarową, płaszczyzna w przestrzeni trójwymiarowej jest hiperpłaszczyzną dwuwymiarową.
Cel determinował cele badania:
1) Przestudiować podstawowe fakty dotyczące wielowymiarowej geometrii analitycznej;
2) Zbadaj cechy konstruowania kostek o wymiarach od 0 do 3;
3) Zbadaj strukturę czterowymiarowego sześcianu;
4) Analitycznie i geometrycznie opisać czterowymiarowy sześcian;
5) Wykonywać modele rozwinięć i rzuty centralne kostek trójwymiarowych i czterowymiarowych.
6) Korzystając z aparatu wielowymiarowej geometrii analitycznej, opisywać trójwymiarowe obiekty powstałe w wyniku przecięcia czterowymiarowego sześcianu z hiperpłaszczyznami równoległymi do jednej z jego trójwymiarowych ścian lub hiperpłaszczyznami prostopadłymi do jego głównej przekątnej.
Uzyskane w ten sposób informacje pozwolą nam lepiej zrozumieć budowę tesseraktu, a także zidentyfikować głębokie analogie w budowie i właściwościach kostek o różnych wymiarach.
Głównym elementem
Najpierw opisujemy aparat matematyczny, z którego będziemy korzystać podczas tego badania.
1) Współrzędne wektora: if, To
2) Równanie hiperpłaszczyzny z wektorem normalnym wygląda jak Tutaj
3) Samoloty i są równoległe wtedy i tylko wtedy, gdy
4) Odległość między dwoma punktami określa się w następujący sposób: jeżeli, To
5) Warunek ortogonalności wektorów:
Przede wszystkim dowiedzmy się, jak opisać czterowymiarowy sześcian. Można to zrobić na dwa sposoby - geometryczny i analityczny.
Jeśli mówimy o geometrycznej metodzie określania, wskazane jest prześledzenie procesu konstruowania kostek, zaczynając od wymiaru zerowego. Sześcian o wymiarze zerowym jest punktem (nawiasem mówiąc, punkt może pełnić także rolę kuli o wymiarze zerowym). Następnie wprowadzamy pierwszy wymiar (oś x) i na odpowiedniej osi zaznaczamy dwa punkty (dwie kostki zerowymiarowe) znajdujące się w odległości 1 od siebie. Rezultatem jest segment - jednowymiarowy sześcian. Zwróćmy od razu uwagę na charakterystyczną cechę: brzegiem (końcami) jednowymiarowego sześcianu (odcinka) są dwie zerowymiarowe sześciany (dwa punkty). Następnie wprowadzamy drugi wymiar (oś rzędnych) i na płaszczyźnieSkonstruujmy dwie jednowymiarowe kostki (dwa segmenty), których końce znajdują się w odległości 1 od siebie (w rzeczywistości jeden z segmentów jest rzutem ortogonalnym drugiego). Łącząc odpowiednie końce segmentów otrzymujemy kwadrat - dwuwymiarowy sześcian. Ponownie zauważmy, że granicę dwuwymiarowego sześcianu (kwadratu) stanowią cztery jednowymiarowe sześciany (cztery segmenty). Na koniec wprowadzamy trzeci wymiar (aplikujemy oś) i konstruujemy w przestrzenidwa kwadraty w taki sposób, że jeden z nich jest rzutem prostopadłym drugiego (odpowiednie wierzchołki kwadratów znajdują się w odległości 1 od siebie). Połączmy odpowiednie wierzchołki segmentami - otrzymamy trójwymiarowy sześcian. Widzimy, że granicę trójwymiarowego sześcianu stanowi sześć dwuwymiarowych sześcianów (sześć kwadratów). Opisane konstrukcje pozwalają zidentyfikować następujący schemat: na każdym krokusześcian wymiarowy „porusza się, zostawiając ślad” wpomiar w odległości 1, przy czym kierunek ruchu jest prostopadły do sześcianu. To formalna kontynuacja tego procesu pozwala nam dojść do koncepcji czterowymiarowego sześcianu. Mianowicie wymusimy przemieszczenie trójwymiarowej kostki w kierunku czwartego wymiaru (prostopadle do sześcianu) na odległość 1. Postępując analogicznie jak poprzednio, czyli łącząc odpowiednie wierzchołki kostek, otrzymamy czterowymiarowy sześcian. Należy zauważyć, że geometrycznie taka konstrukcja w naszej przestrzeni jest niemożliwa (ponieważ jest trójwymiarowa), ale tutaj nie napotykamy żadnych sprzeczności z logicznego punktu widzenia. Przejdźmy teraz do analitycznego opisu czterowymiarowej kostki. Uzyskuje się go również formalnie, stosując analogię. Zatem specyfikacja analityczna zerowymiarowego sześcianu jednostkowego ma postać:
Zadanie analityczne jednowymiarowego sześcianu jednostkowego ma postać:
Zadanie analityczne dwuwymiarowego sześcianu jednostkowego ma postać:
Zadanie analityczne trójwymiarowego sześcianu jednostkowego ma postać:
Teraz bardzo łatwo jest podać analityczną reprezentację czterowymiarowego sześcianu, a mianowicie:
Jak widać, zarówno geometryczne, jak i analityczne metody definiowania czterowymiarowego sześcianu wykorzystywały metodę analogii.
Teraz korzystając z aparatu geometrii analitycznej dowiemy się jaka jest budowa czterowymiarowego sześcianu. Najpierw dowiedzmy się, jakie elementy zawiera. Tutaj znowu możemy posłużyć się analogią (aby postawić hipotezę). Granice sześcianu jednowymiarowego stanowią punkty (kostki zerowymiarowe), sześcianu dwuwymiarowego - segmenty (kostki jednowymiarowe), sześcianu trójwymiarowego - kwadraty (ściany dwuwymiarowe). Można założyć, że granice tesseraktu stanowią trójwymiarowe sześciany. Aby to udowodnić, wyjaśnijmy, co oznaczają wierzchołki, krawędzie i ściany. Wierzchołki sześcianu są jego narożnikami. Oznacza to, że współrzędne wierzchołków mogą być zerami lub jedynekami. W ten sposób ujawnia się związek między wymiarem sześcianu a liczbą jego wierzchołków. Zastosujmy regułę iloczynu kombinatorycznego - od wierzchołkazmierzona kostka ma dokładniewspółrzędne, z których każda jest równa zero lub jeden (niezależnie od wszystkich innych), to w sumie jestszczyty Zatem dla dowolnego wierzchołka wszystkie współrzędne są stałe i mogą być równe Lub . Jeśli ustalimy wszystkie współrzędne (ustawiając każdą z nich równą Lub niezależnie od pozostałych), za wyjątkiem jednego, otrzymujemy linie proste zawierające krawędzie sześcianu. Podobnie jak w poprzednim, możesz policzyć, że są dokładnierzeczy. A jeśli teraz naprawimy wszystkie współrzędne (ustawiając każdą z nich równą Lub , niezależnie od pozostałych), poza kilkoma dwoma, otrzymujemy płaszczyzny zawierające dwuwymiarowe ściany sześcianu. Korzystając z reguły kombinatoryki, stwierdzamy, że dokładnie takrzeczy. Następnie analogicznie - ustalenie wszystkich współrzędnych (wyrównanie każdej z nich). Lub , niezależnie od pozostałych), z wyjątkiem kilku trzech, otrzymujemy hiperpłaszczyzny zawierające trójwymiarowe ściany sześcianu. Stosując tę samą zasadę, obliczamy ich liczbę - dokładnieitp. To wystarczy do naszych badań. Uzyskane wyniki zastosujmy do struktury czterowymiarowego sześcianu, czyli we wszystkich formułach wyprowadzonych, które umieścimy. Zatem czterowymiarowy sześcian ma: 16 wierzchołków, 32 krawędzie, 24 dwuwymiarowe ściany i 8 trójwymiarowych ścian. Dla jasności zdefiniujmy analitycznie wszystkie jego elementy.
Wierzchołki czterowymiarowego sześcianu:
Krawędzie czterowymiarowego sześcianu ():
Dwuwymiarowe ściany czterowymiarowego sześcianu (podobne ograniczenia):
Trójwymiarowe ściany czterowymiarowego sześcianu (podobne ograniczenia):
Teraz, gdy struktura czterowymiarowego sześcianu i metody jej definiowania zostały opisane wystarczająco szczegółowo, przejdźmy do realizacji głównego celu - wyjaśnienia natury poszczególnych sekcji sześcianu. Zacznijmy od elementarnego przypadku, gdy przekroje sześcianu są równoległe do jednej z jego trójwymiarowych ścian. Rozważmy na przykład jego przekroje z hiperpłaszczyznami równoległymi do ścianyZ geometrii analitycznej wiadomo, że dowolny taki przekrój będzie dany równaniemZdefiniujmy analitycznie odpowiednie sekcje:
Jak widać otrzymaliśmy specyfikację analityczną trójwymiarowego sześcianu jednostkowego leżącego w hiperpłaszczyźnie
Aby ustalić analogię, napiszmy przekrój trójwymiarowego sześcianu przez płaszczyznę Otrzymujemy:
To jest kwadrat leżący na płaszczyźnie. Analogia jest oczywista.
Przekroje czterowymiarowego sześcianu za pomocą hiperpłaszczyzndać całkowicie podobne wyniki. Będą to także pojedyncze trójwymiarowe kostki leżące w hiperpłaszczyznach odpowiednio.
Rozważmy teraz przekroje czterowymiarowego sześcianu z hiperpłaszczyznami prostopadłymi do jego głównej przekątnej. Najpierw rozwiążmy ten problem dla trójwymiarowego sześcianu. Korzystając z opisanej powyżej metody definiowania jednostkowego trójwymiarowego sześcianu dochodzi do wniosku, że za główną przekątną można przyjąć np. odcinek o końcach I . Oznacza to, że wektor głównej przekątnej będzie miał współrzędne. Zatem równanie dowolnej płaszczyzny prostopadłej do głównej przekątnej będzie wyglądało następująco:
Ustalmy granice zmiany parametrów. Ponieważ , następnie dodając te nierówności wyraz po wyrazie, otrzymujemy:
Lub .
Jeśli następnie (ze względu na ograniczenia). Podobnie - jeśli, To . Zatem kiedy i kiedy płaszczyzna przecięcia i sześcian mają dokładnie jeden punkt wspólny ( I odpowiednio). Zwróćmy teraz uwagę na następujące kwestie. Jeśli(ponownie ze względu na zmienne ograniczenia). Odpowiednie płaszczyzny przecinają jednocześnie trzy ściany, gdyż w przeciwnym razie płaszczyzna cięcia byłaby równoległa do jednej z nich, co nie ma miejsca zgodnie z warunkiem. Jeśli, wówczas płaszczyzna przecina wszystkie ściany sześcianu. Jeśli, wówczas płaszczyzna przecina ściany. Przedstawmy odpowiednie obliczenia.
Pozwalać Potem samolotprzekracza linię w linii prostej oraz . Co więcej, krawędź. Krawędź płaszczyzna przecina się z linią prostą, I
Pozwalać Potem samolotprzekracza linię:
krawędź w linii prostej oraz .
krawędź w linii prostej oraz .
krawędź w linii prostej oraz .
krawędź w linii prostej oraz .
krawędź w linii prostej oraz .
krawędź w linii prostej oraz .
Tym razem otrzymujemy sześć segmentów, które mają kolejno wspólne końce:
Pozwalać Potem samolotprzekracza linię w linii prostej oraz . Krawędź płaszczyzna przecina się z linią prostą, I . Krawędź płaszczyzna przecina się z linią prostą, I . Oznacza to, że otrzymujemy trzy segmenty, które mają wspólne końce parami:Zatem dla określonych wartości parametrówpłaszczyzna przetnie sześcian wzdłuż regularnego trójkąta z wierzchołkami
Oto kompleksowy opis figur płaskich uzyskanych, gdy sześcian przecina się płaszczyzną prostopadłą do jego głównej przekątnej. Główna idea była następująca. Konieczne jest zrozumienie, które ściany przecina płaszczyzna, wzdłuż jakich zbiorów je przecina i jak te zbiory są ze sobą powiązane. Na przykład, jeśli okazało się, że płaszczyzna przecina dokładnie trzy ściany wzdłuż odcinków, które mają wspólne końce parami, wówczas przekrój jest trójkątem równobocznym (co udowadnia bezpośrednie obliczenie długości odcinków), którego wierzchołkami są te końce segmentów.
Używając tej samej aparatury i tej samej idei studiowania sekcji, w całkowicie analogiczny sposób można wywnioskować następujące fakty:
1) Wektor jednej z głównych przekątnych czterowymiarowego sześcianu jednostkowego ma współrzędne
2) Dowolną hiperpłaszczyznę prostopadłą do głównej przekątnej czterowymiarowego sześcianu można zapisać w postaci.
3) W równaniu siecznej hiperpłaszczyzny parametrmoże zmieniać się od 0 do 4;
4) Kiedy i sieczna hiperpłaszczyzna i czterowymiarowy sześcian mają jeden wspólny punkt ( I odpowiednio);
5) Kiedy przekrój utworzy regularny czworościan;
6) Kiedy w przekroju wynikiem będzie ośmiościan;
7) Kiedy przekrój poprzeczny utworzy regularny czworościan.
Odpowiednio tutaj hiperpłaszczyzna przecina tesserakt wzdłuż płaszczyzny, na której ze względu na ograniczenia zmiennych wyznaczony jest obszar trójkątny (analogia - płaszczyzna przecinała sześcian po linii prostej, na której ze względu na ograniczenia zmiennych, przydzielono segment). W przypadku 5) hiperpłaszczyzna przecina dokładnie cztery trójwymiarowe ściany tesseraktu, czyli otrzymujemy cztery trójkąty, które mają wspólne boki parami, czyli innymi słowy tworzą czworościan (jak to można obliczyć, jest poprawne). W przypadku 6) hiperpłaszczyzna przecina dokładnie osiem trójwymiarowych ścian tesseraktu, czyli otrzymuje się osiem trójkątów, które mają kolejno wspólne boki, innymi słowy tworząc ośmiościan. Przypadek 7) jest całkowicie podobny do przypadku 5).
Zilustrujmy to konkretnym przykładem. Mianowicie badamy przekrój czterowymiarowego sześcianu przez hiperpłaszczyznęZe względu na zmienne ograniczenia ta hiperpłaszczyzna przecina następujące trójwymiarowe ściany: Krawędź przecina się wzdłuż płaszczyznyZe względu na ograniczenia zmiennych mamy:Otrzymujemy obszar trójkątny z wierzchołkamiDalej,otrzymamy trójkątKiedy hiperpłaszczyzna przecina twarzotrzymamy trójkątKiedy hiperpłaszczyzna przecina twarzotrzymamy trójkątZatem wierzchołki czworościanu mają następujące współrzędne. Jak łatwo obliczyć, czworościan ten jest rzeczywiście foremny.
wnioski
Tak więc w trakcie tych badań zbadano podstawowe fakty wielowymiarowej geometrii analitycznej, zbadano cechy konstruowania kostek o wymiarach od 0 do 3, zbadano strukturę czterowymiarowego sześcianu, czterowymiarowy sześcian opisano analitycznie i geometrycznie, wykonano modele zabudowy i rzuty centralne kostek trójwymiarowych i czterowymiarowych, kostki trójwymiarowe opisano analitycznie obiekty powstałe w wyniku przecięcia czterowymiarowego sześcianu z hiperpłaszczyznami równoległymi do jednej z jego trójwymiarowych powierzchnie wymiarowe lub z hiperpłaszczyznami prostopadłymi do głównej przekątnej.
Przeprowadzone badania pozwoliły na zidentyfikowanie głębokich analogii w budowie i właściwościach kostek o różnych wymiarach. Zastosowaną technikę analogii można zastosować w badaniach np.kula wymiarowa lubsympleks wymiarowy. Mianowicie,kulę wymiarową można zdefiniować jako zbiór punktówprzestrzeń wymiarowa w równej odległości od danego punktu, nazywana środkiem kuli. Dalej,sympleks wymiarowy można zdefiniować jako częśćprzestrzeń wymiarowa ograniczona liczbą minimalnąhiperpłaszczyzny wymiarowe. Na przykład sympleks jednowymiarowy to odcinek (część przestrzeni jednowymiarowej ograniczona dwoma punktami), sympleks dwuwymiarowy to trójkąt (część przestrzeni dwuwymiarowej ograniczona trzema liniami), sympleks dwuwymiarowy trójwymiarowy sympleks to czworościan (część trójwymiarowej przestrzeni ograniczona czterema płaszczyznami). Wreszcie,definiujemy sympleks wymiarowy jako częśćprzestrzeń wymiarowa, ograniczonahiperpłaszczyzna wymiaru.
Należy zauważyć, że pomimo licznych zastosowań tesseraktu w niektórych obszarach nauki, badania te nadal mają głównie charakter matematyczny.
Bibliografia
1) Bugrov Ya.S., Nikolsky S.M.Matematyka wyższa, t. 1 – M.: Drop, 2005 – 284 s.
2) Kwantowy. Czterowymiarowy sześcian / Duzhin S., Rubtsov V., nr 6, 1986.
3) Kwantowy. Jak rysować kostka wymiarowa / Demidovich N.B., nr 8, 1974.









