Volá sa nájdenie derivácie danej funkcie f. Derivácia e k mocnine x a exponenciálnej funkcii

V tejto lekcii sa naučíme používať vzorce a pravidlá diferenciácie.

Príklady. Nájdite derivácie funkcií.

1. y = x 7 + x 5 - x 4 + x 3 - x 2 + x - 9. Uplatnenie pravidla ja, vzorce 4, 2 a 1. Dostaneme:

y’=7x 6 +5x4-4x3+3x2-2x+1.

2. y=3x6-2x+5. Riešime podobne, pomocou rovnakých vzorcov a vzorca 3.

y’=3∙6x 5-2=18x 5-2.

Uplatnenie pravidla ja, vzorce 3, 5 A 6 A 1.

Uplatnenie pravidla IV, vzorce 5 A 1 .

V piatom príklade podľa pravidla ja derivácia súčtu sa rovná súčtu derivácií a práve sme našli deriváciu 1. člena (príklad 4 ), preto nájdeme deriváty 2 A 3 podmienky a za 1 summand môžeme hneď napísať výsledok.

Poďme rozlišovať 2 A 3 termíny podľa vzorca 4 . Aby sme to dosiahli, transformujeme korene tretej a štvrtej mocniny v menovateli na mocniny so zápornými exponentmi a potom podľa 4 formule, nájdeme deriváty mocnín.

Pozrite si tento príklad a výsledok. Zachytili ste vzor? Dobre. To znamená, že máme nový vzorec a môžeme ho pridať do našej tabuľky derivátov.

Vyriešme šiesty príklad a odvodíme ďalší vzorec.

Využime pravidlo IV a vzorec 4 . Výsledné zlomky zredukujeme.

Pozrime sa na túto funkciu a jej deriváciu. Vy, samozrejme, rozumiete vzoru a ste pripravení pomenovať vzorec:

Učte sa nové vzorce!

Príklady.

1. Nájdite prírastok argumentu a prírastok funkcie y= x 2, ak bola počiatočná hodnota argumentu rovná 4 a nové - 4,01 .

Riešenie.

Nová hodnota argumentu x=x 0 +Δx. Dosadíme údaje: 4,01=4+Δх, teda prírastok argumentu Δх= 4,01-4 = 0,01. Prírastok funkcie sa podľa definície rovná rozdielu medzi novou a predchádzajúcou hodnotou funkcie, t.j. Ay=f (x 0 + Ax) - f (x 0). Keďže máme funkciu y=x2, To Δу=(x 0 +Δx) 2 - (x 0) 2 =(x 0) 2 +2x 0 · Δx+(Δx) 2 - (x 0) 2 = 2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

odpoveď: prírastok argumentov Δх=0,01; prírastok funkcie Δу=0,0801.

Prírastok funkcie možno nájsť inak: Δy=y(x0+Ax)-y(x0)=y(4,01)-y(4)=4,012-42=16,0801-16=0,0801.

2. Nájdite uhol sklonu dotyčnice ku grafu funkcie y=f(x) v bode x 0, Ak f "(x 0) = 1.

Riešenie.

Hodnota derivátu v bode dotyku x 0 a je hodnotou tangens tangens uhla (geometrický význam derivácie). Máme: f "(x 0) = tanα = 1 → α = 45°, pretože tg45°=1.

odpoveď: dotyčnica ku grafu tejto funkcie zviera s kladným smerom osi Ox uhol rovný 45°.

3. Odvoďte vzorec pre deriváciu funkcie y=xn.

Diferenciácia je činnosť hľadania derivácie funkcie.

Pri hľadaní derivátov použite vzorce, ktoré boli odvodené na základe definície derivátu, rovnakým spôsobom, ako sme odvodili vzorec pre stupeň derivátu: (x n)" = nx n-1.

Toto sú vzorce.

Tabuľka derivátov Bude ľahšie zapamätať si vyslovovaním verbálnych formulácií:

1. Derivácia konštantnej veličiny je nulová.

2. X prvočíslo sa rovná jednej.

3. Konštantný faktor možno vyňať zo znamienka derivácie.

4. Derivácia stupňa sa rovná súčinu exponentu tohto stupňa o stupeň s rovnakým základom, ale exponent je o jeden menší.

5. Derivácia koreňa sa rovná jednej delenej dvoma rovnakými koreňmi.

6. Derivácia jedna delená x sa rovná mínus jedna delená x na druhú.

7. Derivácia sínusu sa rovná kosínusu.

8. Derivácia kosínusu sa rovná mínus sínusu.

9. Derivácia dotyčnice sa rovná jednej delenej druhou mocninou kosínusu.

10. Derivácia kotangensu sa rovná mínus jednej delenej druhou mocninou sínusu.

Učíme pravidlá diferenciácie.

1. Derivácia algebraického súčtu sa rovná algebraickému súčtu derivátov členov.

2. Derivát súčinu sa rovná súčinu derivátu prvého a druhého faktora plus súčinu prvého faktora a derivátu druhého.

3. Derivácia „y“ delená „ve“ sa rovná zlomku, v ktorom je čitateľ „y prvočíslo vynásobené „ve“ mínus „y vynásobené prvočíslom ve“ a menovateľ je „ve na druhú“.

4. Špeciálny prípad vzorca 3.

Poďme sa spolu učiť!

Strana 1 z 1 1

Pri riešení rôznych problémov geometrie, mechaniky, fyziky a iných oblastí vedomostí vznikla potreba použiť rovnaký analytický proces z tejto funkcie y=f(x) získať novú funkciu s názvom derivačná funkcia(alebo jednoducho derivácia) danej funkcie f(x) a je označený symbolom

Proces, ktorým z danej funkcie f(x) získať novú funkciu f" (x), volal diferenciácie a pozostáva z nasledujúcich troch krokov: 1) uveďte argument X prírastok  X a určiť zodpovedajúci prírastok funkcie  y = f(x+ x) -f(x); 2) vytvoriť vzťah

3) počítanie X konštantný a  X0, nájdeme
, ktoré označujeme f" (x), akoby zdôrazňoval, že výsledná funkcia závisí len od hodnoty X, pri ktorej ideme na doraz. Definícia: Derivát y " =f " (x) daná funkcia y=f(x) pre dané x sa nazýva limita pomeru prírastku funkcie k prírastku argumentu za predpokladu, že prírastok argumentu smeruje k nule, ak samozrejme táto limita existuje, t.j. konečný. teda
, alebo

Všimnite si, že ak pre nejakú hodnotu X, napríklad keď x=a, postoj
pri  X0 nesmeruje ku konečnej limite, potom v tomto prípade hovoria, že funkcia f(x) pri x=a(alebo v bode x=a) nemá žiadnu deriváciu alebo nie je v bode diferencovateľná x=a.

2. Geometrický význam derivácie.

Uvažujme graf funkcie y = f (x), diferencovateľnej v blízkosti bodu x 0

f(x)

Uvažujme ľubovoľnú priamku prechádzajúcu bodom na grafe funkcie - bod A(x 0, f (x 0)) a pretínajúci graf v nejakom bode B(x;f(x)). Takáto čiara (AB) sa nazýva sečna. Z ∆ABC: ​​​​AC = ∆x; ВС =∆у; tgβ=∆y/∆x.

Od AC || Ox, potom ALO = BAC = β (ako zodpovedá paralelu). Ale ALO je uhol sklonu sečnice AB ku kladnému smeru osi Ox. To znamená, že tanβ = k je sklon priamky AB.

Teraz znížime ∆х, t.j. ∆х→ 0. V tomto prípade sa bod B priblíži k bodu A podľa grafu a sečna AB sa bude otáčať. Limitnou polohou sečnice AB pri ∆x→ 0 bude priamka (a), nazývaná dotyčnica ku grafu funkcie y = f (x) v bode A.

Ak prejdeme na limitu ako ∆x → 0 v rovnosti tgβ =∆y/∆x, dostaneme
ortg =f "(x 0), keďže
-uhol sklonu dotyčnice ku kladnému smeru osi Ox
, podľa definície derivátu. Ale tg = k je uhlový koeficient dotyčnice, čo znamená k = tg = f "(x 0).

Geometrický význam derivátu je teda nasledujúci:

Derivácia funkcie v bode x 0 rovná sklonu dotyčnice ku grafu funkcie nakreslenej v bode s os x 0 .

3. Fyzikálny význam derivátu.

Zvážte pohyb bodu pozdĺž priamky. Nech je daná súradnica bodu v ľubovoľnom čase x(t). Je známe (z kurzu fyziky), že priemerná rýchlosť za určité časové obdobie sa rovná pomeru vzdialenosti prejdenej za toto časové obdobie k času, t.j.

Vav = ∆x/∆t. Poďme na limitu v poslednej rovnosti ako ∆t → 0.

lim Vav (t) = (t 0) - okamžitá rýchlosť v čase t 0, ∆t → 0.

a lim = ∆x/∆t = x"(t 0) (podľa definície derivátu).

Takže (t) =x"(t).

Fyzikálny význam derivácie je nasledovný: derivácia funkcier = f(X) v bodeX 0 je rýchlosť zmeny funkcief(x) v bodeX 0

Derivácia sa používa vo fyzike na nájdenie rýchlosti zo známej funkcie súradníc v závislosti od času, zrýchlenia zo známej funkcie rýchlosti v závislosti od času.

(t) = x"(t) - rýchlosť,

a(f) = "(t) - zrýchlenie, príp

Ak je známy zákon pohybu hmotného bodu v kruhu, potom je možné nájsť uhlovú rýchlosť a uhlové zrýchlenie počas rotačného pohybu:

φ = φ(t) - zmena uhla v čase,

ω = φ"(t) - uhlová rýchlosť,

ε = φ"(t) - uhlové zrýchlenie, alebo ε = φ"(t).

Ak je známy zákon o rozdelení hmoty nehomogénnej tyče, potom možno nájsť lineárnu hustotu nehomogénnej tyče:

m = m(x) - hmotnosť,

x  , l - dĺžka tyče,

p = m"(x) - lineárna hustota.

Pomocou derivácie sa riešia problémy z teórie pružnosti a harmonických kmitov. Teda podľa Hookovho zákona

F = -kx, x – premenná súradnica, k – koeficient pružnosti pružiny. Ak dáme ω 2 =k/m, dostaneme diferenciálnu rovnicu pružinového kyvadla x"(t) + ω 2 x(t) = 0,

kde ω = √k/√m frekvencia kmitov (l/c), k - tuhosť pružiny (H/m).

Rovnica v tvare y" + ω 2 y = 0 sa nazýva rovnica harmonických kmitov (mechanických, elektrických, elektromagnetických). Riešením takýchto rovníc je funkcia

y = Asin(ωt + φ 0) alebo y = Acos(ωt + φ 0), kde

A - amplitúda kmitov, ω - cyklická frekvencia,

φ 0 - počiatočná fáza.

Lekcia na tému: "Čo je to derivát? Definícia derivátu"

Dodatočné materiály
Vážení používatelia, nezabudnite zanechať svoje komentáre, recenzie, priania! Všetky materiály boli skontrolované antivírusovým programom.

Učebné pomôcky a simulátory v internetovom obchode Integral pre 10. ročník
Algebraické úlohy s parametrami, ročníky 9–11
Softvérové ​​prostredie "1C: Mathematical Constructor 6.1"

Čo budeme študovať:
1. Úvod do pojmu derivát.
2. Trochu histórie.

4. Derivácia na grafe funkcie. Geometrický význam derivácie.

6. Diferenciácia funkcie.
7. Príklady.

Úvod do pojmu derivát

Existuje veľa problémov, ktoré majú úplne odlišný význam, ale existujú matematické modely, ktoré nám umožňujú vypočítať riešenia našich problémov úplne rovnakým spôsobom. Napríklad, ak vezmeme do úvahy úlohy ako:

A) Existuje bankový účet, ktorý sa neustále mení raz za pár dní, suma neustále rastie, musíte zistiť, akou rýchlosťou účet rastie.
b) Továreň vyrába cukríky, neustále sa zvyšuje produkcia cukríkov, zistite, ako rýchlo sa zvyšuje nárast cukríkov.
c) Rýchlosť auta v určitom okamihu t, ak je známa poloha auta a pohybuje sa priamočiaro.
d) Dostaneme graf funkcie a v určitom bode sa k nemu nakreslí dotyčnica, potrebujeme nájsť dotyčnicu uhla sklonu k dotyčnici.
Formulácia našich problémov je úplne iná a zdá sa, že sú riešené úplne inými spôsobmi, ale matematici prišli na to, ako vyriešiť všetky tieto problémy úplne rovnakým spôsobom. Bol zavedený pojem derivát.

Trochu histórie

Termín derivácia zaviedol veľký matematik Lagrange, preklad do ruštiny pochádza z francúzskeho slova derivee a zaviedol aj modernú notáciu pre deriváciu, o ktorej budeme uvažovať neskôr.
Leibniz a Newton sa vo svojich prácach zaoberali konceptom derivácie, uplatnenie nášho termínu našli v geometrii a mechanike.
O niečo neskôr sa dozvieme, že derivácia je určená cez limitu, no v dejinách matematiky existuje mierny paradox. Matematici sa naučili vypočítať deriváciu skôr, ako zaviedli pojem limita a skutočne pochopili, čo je derivácia.

Nech je funkcia y=f(x) definovaná na určitom intervale obsahujúcom určitý bod x0. Prírastok argumentu Δx neopustí náš interval. Nájdite prírastok Δy a zostavme pomer Δy/Δx; ak existuje limita tohto pomeru, pretože Δx má tendenciu k nule, potom sa táto limita nazýva derivácia funkcie y=f(x) v bode x0 a označuje sa f'(x0).

Pokúsme sa vysvetliť, čo je derivát v nematematickom jazyku:
V matematickom jazyku: derivácia je limit pomeru prírastku funkcie k prírastku jej argumentu, keď prírastok argumentu smeruje k nule.
V bežnom jazyku: derivácia je rýchlosť zmeny funkcie v bode x0.
Pozrime sa na grafy troch funkcií:

Chlapci, ktorá krivka podľa vás rastie rýchlejšie?
Odpoveď sa zdá každému jasná: 1 krivka rastie rýchlejšie ako ostatné. Pozeráme sa na to, ako strmo stúpa funkčný graf. Inými slovami, ako rýchlo sa mení súradnica so zmenou x. Tá istá funkcia v rôznych bodoch môže mať rôzne derivačné hodnoty - to znamená, že sa môže meniť rýchlejšie alebo pomalšie.

Derivácia na grafe funkcie. Geometrický význam derivácie

Teraz sa pozrime, ako nájsť deriváciu pomocou funkčných grafov:


Pozrime sa na náš graf funkcie: Nakreslíme dotyčnicu ku grafu funkcie v bode s osou x0. Dotyčnica a graf našej funkcie sa dotýkajú v bode A. Musíme odhadnúť, ako strmo stúpa graf funkcie. Výhodná hodnota je tangens tangens uhla.

Definícia. Derivácia funkcie v bode x0 sa rovná dotyčnici dotyčnicového uhla nakresleného ku grafu funkcie v tomto bode.

Uhol dotyčnice je vybraný ako uhol medzi dotyčnicou a kladným smerom osi x.
A tak sa derivácia našej funkcie rovná:

A teda derivácia v bode x0 sa rovná dotyčnici dotyčnicového uhla, to je geometrický význam derivácie.

Algoritmus na nájdenie derivácie funkcie y=f(x).
a) Opravte hodnotu x, nájdite f(x).
b) Nájdite prírastok argumentu x+ Δx a hodnotu prírastku funkcie f(x+ Δx).
c) Nájdite prírastok funkcie Δy= f(x+ Δx)-f(x).
d) Zostavte pomer: Δy/Δx
e) Vypočítajte

Toto je derivát našej funkcie.

Diferenciácia funkcie

Ak funkcia y=f(x) má deriváciu v bode x, potom sa nazýva diferencovateľná v bode x. Proces hľadania derivácie sa nazýva diferenciácia funkcie y=f(x).
Vráťme sa k problematike kontinuity funkcie. Ak je funkcia v určitom bode diferencovateľná, potom je možné ku grafu funkcie v tomto bode nakresliť dotyčnicu; funkcia nemôže mať v tomto bode diskontinuitu, potom jednoducho nemožno nakresliť dotyčnicu.
A tak si vyššie uvedené zapíšeme ako definíciu:
Definícia. Ak je funkcia diferencovateľná v bode x, potom je v tomto bode spojitá.
Ak je však funkcia v bode spojitá, neznamená to, že je v tomto bode diferencovateľná. Napríklad funkcia y=|x| v bode x=0 je spojitý, ale tangenta sa nedá nakresliť, čo znamená, že derivácia neexistuje.

Príklady derivátov

Nájdite deriváciu funkcie: y=3x
Riešenie:
Použijeme derivačný vyhľadávací algoritmus.
1) Pre pevnú hodnotu x je funkčná hodnota y=3x
2) V bode x+ Δx, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) Nájdite prírastok funkcie: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δ

Derivát je najdôležitejší pojem v matematickej analýze. Charakterizuje zmenu funkcie argumentu X v určitom okamihu. Okrem toho samotná derivácia je funkciou argumentu X

Derivácia funkcie v bode je limit (ak existuje a je konečný) pomeru prírastku funkcie k prírastku argumentu za predpokladu, že prírastok má tendenciu k nule.

Najčastejšie používané sú nasledujúce derivačný zápis :

Príklad 1 Využiť definícia derivátu, nájdite deriváciu funkcie

Riešenie. Z definície derivátu vyplýva nasledujúca schéma jeho výpočtu.

Dajme argumentu prírastok (delta) a nájdime prírastok funkcie:

Nájdite pomer prírastku funkcie k prírastku argumentu:

Vypočítajme limit tohto pomeru za predpokladu, že prírastok argumentu má tendenciu k nule, teda derivácii požadovanej v probléme:

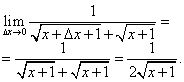
Fyzikálny význam derivátu

TO pojem derivát viedli k štúdiu Galilea Galileiho zákona o voľnom páde telies a v širšom zmysle - problému okamžitej rýchlosti nerovnomerného priamočiareho pohybu bodu.

Nechajte kamienok zdvihnúť a potom uvoľniť z pokoja. Cesta s prešiel v čase t, je funkciou času, tzn. s = s(t). Ak je daný zákon pohybu bodu, potom je možné určiť priemernú rýchlosť za ľubovoľné časové obdobie. Nech je v danom momente kamienok v pozícii A, a momentálne - v pozícii B. Počas určitého obdobia (od t to ) bod prešiel cestou . Preto priemerná rýchlosť pohybu za toto časové obdobie, ktorú označujeme , je

.

Pohyb voľne padajúceho telesa je však zjavne nerovnomerný. Rýchlosť v pád sa neustále zvyšuje. A priemerná rýchlosť už nestačí na charakterizáciu rýchlosti pohybu na rôznych úsekoch trasy. Čím je časový úsek kratší, tým je táto charakteristika presnejšia. Preto sa zavádza tento pojem: okamžitá rýchlosť priamočiareho pohybu (alebo rýchlosť v danom časovom okamihu t) sa nazýva priemerná povolená rýchlosť pri:

(za predpokladu, že táto hranica existuje a je konečná).

Ukazuje sa teda, že okamžitá rýchlosť je hranicou pomeru prírastku funkcie s(t) na prírastok argumentu t at Toto je derivát, ktorý sa vo všeobecnosti píše takto:.

.

Riešenie naznačeného problému je fyzikálny význam derivátu . Takže derivácia funkcie y=f(X) v bode X sa nazýva limita (ak existuje a je konečná) prírastku funkcie k prírastku argumentu za predpokladu, že tento má tendenciu k nule.

Príklad 2 Nájdite deriváciu funkcie

Riešenie. Z definície derivátu vyplýva nasledujúca schéma jeho výpočtu.

Krok 1. Zvýšme argument a nájdime

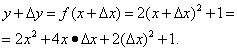
Krok 2. Nájdite prírastok funkcie:

Krok 3. Nájdite pomer prírastku funkcie k prírastku argumentu:

Krok 4. Vypočítajte limit tohto pomeru v , čiže deriváciu:

Geometrický význam derivácie

Nech je funkcia definovaná na intervale a nech je bod M na grafe funkcie zodpovedá hodnote argumentu a bodu R– význam. Poďme kresliť cez body M A R priamku a nazvite ju sekanta. Označme uhlom medzi sečnicou a osou. Je zrejmé, že tento uhol závisí od .

Ak existuje

prechod cez bod sa nazýva medzná poloha sečny PÁN o (alebo o ).

Tangenta ku grafu funkcie v bode M nazývaná limitná poloha sečny PÁN at , or , ktorý je rovnaký v .

Z definície vyplýva, že na existenciu dotyčnice stačí, že existuje limita

,

a limit sa rovná uhlu sklonu dotyčnice k osi.

Teraz uveďme presnú definíciu dotyčnice.

Tangenta ku grafu funkcie v bode je priamka prechádzajúca bodom a majúca sklon, t.j. priamka, ktorej rovnica

Z tejto definície vyplýva, že derivácia funkcie sa rovná sklonu dotyčnice ku grafu tejto funkcie v bode s osou X. Toto je geometrický význam derivácie.

Úloha B9 poskytuje graf funkcie alebo derivácie, z ktorej musíte určiť jednu z nasledujúcich veličín:

1. Hodnota derivátu v určitom bode x 0,
2. Maximálny alebo minimálny počet bodov (extrémne body),
3. Intervaly rastúcich a klesajúcich funkcií (intervaly monotónnosti).

Funkcie a derivácie uvedené v tomto probléme sú vždy spojité, čo značne uľahčuje riešenie. Napriek tomu, že úloha patrí do časti matematickej analýzy, zvládnu ju aj najslabší študenti, keďže tu nie sú potrebné žiadne hlboké teoretické znalosti.

Na nájdenie hodnoty derivácie, extrémnych bodov a intervalov monotónnosti existujú jednoduché a univerzálne algoritmy – o všetkých sa bude diskutovať nižšie.

Pozorne si prečítajte podmienky úlohy B9, aby ste sa vyhli hlúpym chybám: niekedy narazíte na dosť zdĺhavé texty, ale dôležitých podmienok, ktoré ovplyvňujú priebeh riešenia, je málo.

Výpočet hodnoty derivátu. Dvojbodová metóda

Ak je problému daný graf funkcie f(x), dotyčnica k tomuto grafu v určitom bode x 0, a je potrebné nájsť hodnotu derivácie v tomto bode, použije sa nasledujúci algoritmus:

1. Nájdite dva „adekvátne“ body na dotyčnicovom grafe: ich súradnice musia byť celé číslo. Označme tieto body ako A (x 1 ; y 1) a B (x 2 ; y 2). Zapíšte si súradnice správne – ide o kľúčový bod riešenia a akákoľvek chyba tu povedie k nesprávnej odpovedi.
2. Keď poznáme súradnice, je ľahké vypočítať prírastok argumentu Δx = x 2 − x 1 a prírastok funkcie Δy = y 2 − y 1 .
3. Nakoniec nájdeme hodnotu derivácie D = Δy/Δx. Inými slovami, musíte vydeliť prírastok funkcie prírastkom argumentu – a toto bude odpoveď.

Ešte raz si všimnime: body A a B treba hľadať presne na dotyčnici, a nie na grafe funkcie f(x), ako sa to často stáva. Dotyková čiara bude nevyhnutne obsahovať aspoň dva takéto body - inak nebude problém správne formulovaný.

Zvážte body A (−3; 2) a B (−1; 6) a nájdite prírastky:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Zistime hodnotu derivácie: D = Δy/Δx = 4/2 = 2.

Úloha. Na obrázku je znázornený graf funkcie y = f(x) a dotyčnica k nej v bode s os x 0. Nájdite hodnotu derivácie funkcie f(x) v bode x 0 .

Zvážte body A (0; 3) a B (3; 0), nájdite prírastky:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Teraz nájdeme hodnotu derivácie: D = Δy/Δx = −3/3 = −1.

Úloha. Na obrázku je znázornený graf funkcie y = f(x) a dotyčnica k nej v bode s os x 0. Nájdite hodnotu derivácie funkcie f(x) v bode x 0 .

Zvážte body A (0; 2) a B (5; 2) a nájdite prírastky:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Zostáva nájsť hodnotu derivácie: D = Δy/Δx = 0/5 = 0.

Z posledného príkladu môžeme sformulovať pravidlo: ak je dotyčnica rovnobežná s osou OX, derivácia funkcie v bode dotyku je nulová. V tomto prípade nemusíte ani nič počítať - stačí sa pozrieť na graf.

Výpočet maximálneho a minimálneho počtu bodov

Niekedy namiesto grafu funkcie dáva úloha B9 graf derivácie a vyžaduje nájdenie maximálneho alebo minimálneho bodu funkcie. V tejto situácii je dvojbodová metóda zbytočná, ale existuje iný, ešte jednoduchší algoritmus. Najprv si definujme terminológiu:

1. Bod x 0 sa nazýva maximálny bod funkcie f(x), ak v niektorom okolí tohto bodu platí nerovnosť: f(x 0) ≥ f(x).
2. Bod x 0 sa nazýva minimálny bod funkcie f(x), ak v niektorom okolí tohto bodu platí nerovnosť: f(x 0) ≤ f(x).

Ak chcete nájsť maximum a minimum bodov z derivačného grafu, postupujte podľa týchto krokov:

1. Prekreslite derivačný graf a odstráňte všetky nepotrebné informácie. Ako ukazuje prax, nepotrebné údaje len zasahujú do rozhodnutia. Preto na súradnicovej osi označíme nuly derivácie - a je to.
2. Zistite znamienka derivácie na intervaloch medzi nulami. Ak je pre nejaký bod x 0 známe, že f'(x 0) ≠ 0, potom sú možné len dve možnosti: f'(x 0) ≥ 0 alebo f'(x 0) ≤ 0. Znamienko derivácie je ľahko určiť z pôvodného nákresu: ak derivačný graf leží nad osou OX, potom f'(x) ≥ 0. A naopak, ak derivačný graf leží pod osou OX, potom f'(x) ≤ 0.
3. Opäť skontrolujeme nuly a znamienka derivácie. Tam, kde sa znamienko zmení z mínus na plus, je minimálny bod. Naopak, ak sa znamienko derivácie zmení z plus na mínus, ide o maximálny bod. Počítanie sa vždy vykonáva zľava doprava.

Táto schéma funguje len pre spojité funkcie - v probléme B9 nie sú žiadne iné.

Úloha. Na obrázku je znázornený graf derivácie funkcie f(x) definovanej na intervale [−5; 5]. Nájdite minimálny bod funkcie f(x) na tomto segmente.

Zbavme sa nepotrebných informácií a ponechajme len hranice [−5; 5] a nuly derivácie x = −3 a x = 2,5. Všímame si aj tieto znaky:

Je zrejmé, že v bode x = −3 sa znamienko derivácie zmení z mínus na plus. Toto je minimálny bod.

Úloha. Na obrázku je znázornený graf derivácie funkcie f(x) definovanej na intervale [−3; 7]. Nájdite maximálny bod funkcie f(x) na tomto segmente.

Prekreslíme graf a ponecháme len hranice [−3; 7] a nuly derivácie x = −1,7 a x = 5. Všimnime si znamienka derivácie na výslednom grafe. Máme:

Je zrejmé, že v bode x = 5 sa znamienko derivácie zmení z plus na mínus - to je maximálny bod.

Úloha. Na obrázku je znázornený graf derivácie funkcie f(x), definovanej na intervale [−6; 4]. Nájdite maximálny počet bodov funkcie f(x) patriacich segmentu [−4; 3].

Z podmienok úlohy vyplýva, že stačí uvažovať len časť grafu obmedzenú úsečkou [−4; 3]. Zostavíme preto nový graf, na ktorom vyznačíme len hranice [−4; 3] a nuly derivácie v ňom. Konkrétne body x = −3,5 a x = 2. Dostaneme:

Na tomto grafe je len jeden maximálny bod x = 2. Práve v tomto bode sa mení znamienko derivácie z plus na mínus.

Malá poznámka o bodoch s neceločíselnými súradnicami. Napríklad v poslednej úlohe bol uvažovaný bod x = −3,5, ale s rovnakým úspechom môžeme vziať x = −3,4. Ak je problém zostavený správne, takéto zmeny by nemali ovplyvniť odpoveď, pretože body „bez trvalého bydliska“ sa priamo nezúčastňujú na riešení problému. Samozrejme, tento trik nebude fungovať s celočíselnými bodmi.

Hľadanie intervalov rastúcich a klesajúcich funkcií

V takom probléme, ako je maximálny a minimálny bod, sa navrhuje použiť derivačný graf na nájdenie oblastí, v ktorých sa samotná funkcia zvyšuje alebo znižuje. Najprv si definujme, čo je zvyšovanie a znižovanie:

1. O funkcii f(x) sa hovorí, že je rastúca na segmente, ak pre ľubovoľné dva body x 1 a x 2 z tohto segmentu platí nasledujúce tvrdenie: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Inými slovami, čím väčšia je hodnota argumentu, tým väčšia je hodnota funkcie.
2. O funkcii f(x) sa hovorí, že je na segmente klesajúca, ak pre ľubovoľné dva body x 1 a x 2 z tohto segmentu platí nasledujúce tvrdenie: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Tie. Väčšia hodnota argumentu zodpovedá menšej hodnote funkcie.

Formulujme dostatočné podmienky na zvýšenie a zníženie:

1. Aby spojitá funkcia f(x) na segmente vzrástla, stačí, aby jej derivácia vo vnútri segmentu bola kladná, t.j. f’(x) ≥ 0.
2. Aby sa spojitá funkcia f(x) na segmente zmenšila, stačí, aby jej derivácia vo vnútri segmentu bola záporná, t.j. f'(x) ≤ 0.

Prijmime tieto vyhlásenia bez dôkazov. Získame tak schému na nájdenie intervalov zvyšovania a znižovania, ktorá je v mnohom podobná algoritmu na výpočet extrémnych bodov:

1. Odstráňte všetky nepotrebné informácie. V pôvodnom grafe derivácie nás primárne zaujímajú nuly funkcie, preto necháme len tie.
2. Označte znamienka derivácie v intervaloch medzi nulami. Kde f'(x) ≥ 0, funkcia sa zvyšuje a kde f'(x) ≤ 0 sa znižuje. Ak problém nastavuje obmedzenia na premennú x, dodatočne ich označíme na novom grafe.
3. Teraz, keď poznáme správanie funkcie a obmedzenia, zostáva vypočítať množstvo požadované v úlohe.

Úloha. Na obrázku je znázornený graf derivácie funkcie f(x) definovanej na intervale [−3; 7,5]. Nájdite intervaly poklesu funkcie f(x). Vo svojej odpovedi uveďte súčet celých čísel zahrnutých v týchto intervaloch.

Ako obvykle, prekreslíme graf a označíme hranice [−3; 7,5], ako aj nuly derivácie x = −1,5 a x = 5,3. Potom si všimneme znaky derivácie. Máme:

Keďže derivácia je záporná na intervale (− 1,5), ide o interval klesajúcej funkcie. Zostáva sčítať všetky celé čísla, ktoré sú v tomto intervale:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Úloha. Na obrázku je znázornený graf derivácie funkcie f(x), definovanej na intervale [−10; 4]. Nájdite intervaly nárastu funkcie f(x). Vo svojej odpovedi uveďte dĺžku najväčšieho z nich.

Zbavme sa nepotrebných informácií. Ponechajme len hranice [−10; 4] a nuly derivácie, ktoré boli tentokrát štyri: x = −8, x = −6, x = −3 a x = 2. Označme znamienka derivácie a získame nasledujúci obrázok:

Zaujímajú nás intervaly rastúcej funkcie, t.j. také, kde f’(x) ≥ 0. Na grafe sú dva takéto intervaly: (−8; −6) a (−3; 2). Vypočítajme ich dĺžku:
l 1 = − 6 − (−8) = 2;
l2 = 2 − (−3) = 5.

Keďže potrebujeme nájsť dĺžku najväčšieho z intervalov, zapíšeme si ako odpoveď hodnotu l 2 = 5.