19. septembra 2009
Tesseract (zo starogréčtiny τέσσερες ἀκτῖνες - štyri lúče) je štvorrozmerná hyperkocka - analóg kocky v štvorrozmernom priestore.
Obraz je projekcia (perspektíva) štvorrozmernej kocky do trojrozmerného priestoru.
Podľa Oxfordského slovníka slovo „tesseract“ vymyslel a použil v roku 1888 Charles Howard Hinton (1853–1907) vo svojej knihe A New Age of Thought. Neskôr niektorí ľudia nazvali tú istú postavu „tetracube“.
Geometria
Obyčajný tesseract v euklidovskom štvorrozmernom priestore je definovaný ako konvexný obal bodov (±1, ±1, ±1, ±1). Inými slovami, môže byť reprezentovaný ako nasledujúca množina:
Tesseract je ohraničený ôsmimi nadrovinami, ktorých priesečník so samotným tesseractom definuje jeho trojrozmerné plochy (čo sú obyčajné kocky). Každý pár nerovnobežných 3D plôch sa pretína a vytvára 2D plochy (štvorce) atď. Nakoniec má tesseract 8 3D plôch, 24 2D plôch, 32 hrán a 16 vrcholov.
Populárny popis
Skúsme si predstaviť, ako bude vyzerať hyperkocka bez toho, aby sme opustili trojrozmerný priestor.
V jednorozmernom „priestore“ - na priamke - vyberieme úsečku AB dĺžky L. Na dvojrozmernej rovine vo vzdialenosti L od AB nakreslíme úsečku DC rovnobežnú s ňou a ich konce spojíme. Výsledkom je štvorec ABCD. Opakovaním tejto operácie s rovinou získame trojrozmernú kocku ABCDHEFG. A posunutím kocky v štvrtom rozmere (kolmo na prvé tri) o vzdialenosť L dostaneme hyperkocku ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Construction_tesseract.PNG
Jednorozmerný segment AB slúži ako strana dvojrozmerného štvorca ABCD, štvorec - ako strana kocky ABCDHEFG, ktorá bude naopak stranou štvorrozmernej hyperkocky. Priamy segment má dva hraničné body, štvorec má štyri vrcholy a kocka osem. V štvorrozmernej hyperkocke teda bude 16 vrcholov: 8 vrcholov pôvodnej kocky a 8 posunutého vo štvrtom rozmere. Má 32 hrán – každá z nich 12 udáva počiatočnú a konečnú polohu pôvodnej kocky a ďalších 8 hrán „kreslí“ jej osem vrcholov, ktoré sa presunuli do štvrtej dimenzie. Rovnaké uvažovanie možno urobiť pre steny hyperkocky. V dvojrozmernom priestore je len jeden (samotný štvorec), kocka ich má 6 (dve tváre z posunutého štvorca a ďalšie štyri, ktoré opisujú jeho strany). Štvorrozmerná hyperkocka má 24 štvorcových plôch – 12 políčok pôvodnej kocky v dvoch polohách a 12 políčok od jej dvanástich hrán.
Podobným spôsobom môžeme pokračovať v úvahách pre hyperkocky väčšieho počtu rozmerov, no oveľa zaujímavejšie je sledovať, ako bude štvorrozmerná hyperkocka vyzerať pre nás, obyvateľov trojrozmerného priestoru. Na to použijeme už známu metódu analógií.
Tesseract sa rozbaľuje
Vezmeme drôtenú kocku ABCDHEFG a pozrieme sa na ňu jedným okom zo strany okraja. Uvidíme a môžeme nakresliť dva štvorce na rovine (jej blízke a vzdialené okraje), spojené štyrmi čiarami - bočnými okrajmi. Podobne štvorrozmerná hyperkocka v trojrozmernom priestore bude vyzerať ako dve kubické „škatule“ vložené do seba a spojené ôsmimi hranami. V tomto prípade sa samotné „boxy“ – trojrozmerné tváre – premietnu do „nášho“ priestoru a čiary, ktoré ich spájajú, sa roztiahnu do štvrtej dimenzie. Môžete si tiež skúsiť predstaviť kocku nie v projekcii, ale v priestorovom obrázku.
Tak ako je trojrozmerná kocka tvorená štvorcom posunutým o dĺžku jeho plochy, kocka posunutá do štvrtého rozmeru vytvorí hyperkocku. Je ohraničený ôsmimi kockami, ktoré budú v perspektíve vyzerať ako nejaký dosť zložitý obrazec. Časť, ktorá zostala v „našom“ priestore, je nakreslená plnými čiarami a časť, ktorá prešla do hyperpriestoru, je nakreslená bodkovanými čiarami. Samotná štvorrozmerná hyperkocka pozostáva z nekonečného počtu kociek, rovnako ako trojrozmernú kocku možno „rozrezať“ na nekonečné množstvo plochých štvorcov.
Rozrezaním šiestich plôch trojrozmernej kocky ju môžete rozložiť na plochú postavu - vývoj. Bude mať štvorec na každej strane pôvodnej tváre plus jeden ďalší - tvár oproti nemu. A trojrozmerný vývoj štvorrozmernej hyperkocky bude pozostávať z pôvodnej kocky, šiestich kociek, ktoré z nej „rastú“, plus jednej ďalšej - konečnej „hyperface“.
Vlastnosti tesseractu predstavujú pokračovanie vlastností geometrických útvarov nižšej dimenzie do štvorrozmerného priestoru.
Projekcie
Do dvojrozmerného priestoru
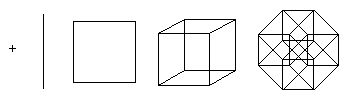
Táto štruktúra je ťažko predstaviteľná, ale je možné premietnuť tesseract do dvojrozmerných alebo trojrozmerných priestorov. Okrem toho premietanie do roviny uľahčuje pochopenie polohy vrcholov hyperkocky. Týmto spôsobom je možné získať obrázky, ktoré už neodrážajú priestorové vzťahy v rámci tesseractu, ale ilustrujú štruktúru spojenia vrcholov, ako v nasledujúcich príkladoch:
Do trojrozmerného priestoru
Projekcia tesseractu do trojrozmerného priestoru predstavuje dve vnorené trojrozmerné kocky, ktorých zodpovedajúce vrcholy sú spojené segmentmi. Vnútorná a vonkajšia kocka majú v trojrozmernom priestore rôzne veľkosti, no v štvorrozmernom priestore sú to rovnaké kocky. Na pochopenie rovnosti všetkých kociek tesseractu bol vytvorený rotujúci model tesseractu.
Šesť zrezaných pyramíd pozdĺž okrajov tesseractu sú obrazy rovnakých šiestich kociek.
Stereo pár
Stereo pár tesseractu je znázornený ako dve projekcie do trojrozmerného priestoru. Tento obrázok tesseractu bol navrhnutý tak, aby predstavoval hĺbku ako štvrtý rozmer. Stereo pár sa pozerá tak, že každé oko vidí iba jeden z týchto obrázkov, objaví sa stereoskopický obraz, ktorý reprodukuje hĺbku tesseractu.
Tesseract sa rozbaľuje
Povrch tesseractu sa dá rozložiť na osem kociek (podobne ako sa dá povrch kocky rozložiť na šesť štvorcov). Existuje 261 rôznych dizajnov tesseract. Rozvinutie tesseractu možno vypočítať vynesením spojených uhlov do grafu.
Tesseract v umení
V „New Abbott Plain“ od Edwiny A. hyperkocka pôsobí ako rozprávač.
V jednej epizóde The Adventures of Jimmy Neutron: "Boy Genius" Jimmy vynájde štvorrozmernú hyperkocku identickú so skladacou skrinkou z Heinleinovho románu Glory Road z roku 1963.
Robert E. Heinlein spomenul hyperkocky najmenej v troch sci-fi príbehoch. V The House of Four Dimensions (The House That Teal Built) (1940) opísal dom postavený ako nezabalený tesseract.
Heinleinov román Glory Road opisuje jedlá nadmernej veľkosti, ktoré boli väčšie zvnútra ako zvonku.
Príbeh Henryho Kuttnera „Mimsy Were the Borogoves“ opisuje vzdelávaciu hračku pre deti z ďalekej budúcnosti, podobnú štruktúre ako tesseract.
V románe Alexa Garlanda (1999) sa termín „tesseract“ používa na trojrozmerné rozvinutie štvorrozmernej hyperkocky, a nie samotnej hyperkocky. Toto je metafora navrhnutá tak, aby ukázala, že kognitívny systém musí byť širší ako poznateľný.
Dej hry Cube 2: Hypercube sa sústreďuje na osem cudzincov uväznených v „hyperkocke“ alebo sieti spojených kociek.
Televízny seriál Andromeda používa generátory tesseract ako zápletkové zariadenie. Sú primárne určené na manipuláciu s priestorom a časom.
Obraz „Ukrižovanie“ (Corpus Hypercubus) od Salvadora Dalího (1954)
Komiks Nextwave zobrazuje vozidlo, ktoré obsahuje 5 zón tesseract.
Na albume Voivod Nothingface sa jedna zo skladieb volá „In my hypercube“.
V románe Anthonyho Pearcea Route Cube sa jeden z obiehajúcich mesiacov Medzinárodnej asociácie pre rozvoj nazýva tesseract, ktorý bol stlačený do 3 rozmerov.
V sérii „Black Hole School“ v tretej sezóne je epizóda „Tesseract“. Lucas stlačí tajné tlačidlo a škola sa začne formovať ako matematický tesseract.
Termín „tesseract“ a jeho odvodený výraz „tesserate“ sa nachádzajú v príbehu „A Wrinkle in Time“ od Madeleine L’Engle.
Hyperkocka a platónske telesá
Modelujte skrátený dvadsaťsten („futbalovú loptu“) v systéme „Vektor“.
v ktorej je každý päťuholník ohraničený šesťuholníkmi
Skrátený dvadsaťsten možno získať odrezaním 12 vrcholov, aby sa vytvorili tváre vo forme pravidelných päťuholníkov. V tomto prípade sa počet vrcholov nového mnohostenu zväčší 5-krát (12×5=60), 20 trojuholníkových plôch sa zmení na pravidelné šesťuholníky (celkom tváre budú 20+12=32), A počet hrán sa zvýši na 30+12×5=90.







Kroky na konštrukciu skráteného dvadsaťstenu v systéme Vector
Postavy v 4-rozmernom priestore.
 --à
--à

 --à
?
--à
?
Napríklad daná kocka a hyperkocka. Hyperkocka má 24 stien. To znamená, že 4-rozmerný osemsten bude mať 24 vrcholov. Hoci nie, hyperkocka má 8 plôch kociek – každá má stred vo svojom vrchole. To znamená, že 4-rozmerný osemsten bude mať 8 vrcholov, čo je ešte ľahšie.


4-rozmerný osemsten. Pozostáva z ôsmich rovnostranných a rovnakých štvorstenov,
spojené štyrmi v každom vrchole.






Ryža. Pokus o simuláciu
hypersféra-hypersféra v systéme Vector
Predná - zadná strana - gule bez skreslenia. Ďalších šesť guľôčok možno definovať cez elipsoidy alebo kvadratické plochy (cez 4 obrysové čiary ako generátory) alebo cez plochy (najskôr definované pomocou generátorov).


Viac techník na „vybudovanie“ hypersféry
- rovnaká „futbalová lopta“ v 4-rozmernom priestore
Dodatok 2
Pre konvexné mnohosteny existuje vlastnosť, ktorá súvisí s počtom jeho vrcholov, hrán a plôch, ktorú v roku 1752 dokázal Leonhard Euler a ktorá sa nazýva Eulerova veta.
Pred jeho formulovaním zvážte nám známe mnohosteny a vyplňte nasledujúcu tabuľku, v ktorej B je počet vrcholov, P - hrán a G - plôch daného mnohostenu:
|
Názov mnohostenu |
|||
|
Trojuholníková pyramída |
|||
|
Štvorhranná pyramída |
|||
|
Trojuholníkový hranol |
|||
|
Štvorhranný hranol |
|||
|
n-uhoľná pyramída |
n+1 |
2n |
n+1 |
|
n-uhlíkový hranol |
2n |
3n |
n+2 |
|
n-uhlie skrátené pyramída |
2n |
3n |
n+2 |
Z tejto tabuľky je hneď zrejmé, že pre všetky vybrané mnohosteny platí rovnosť B - P + G = 2. Ukazuje sa, že táto rovnosť platí nielen pre tieto mnohosteny, ale aj pre ľubovoľný konvexný mnohosten.
Eulerova veta. Pre každý konvexný mnohosten platí rovnosť
B – P + G = 2,
kde B je počet vrcholov, P je počet hrán a G je počet plôch daného mnohostenu.
Dôkaz. Na dôkaz tejto rovnosti si predstavte povrch tohto mnohostenu vyrobený z elastického materiálu. Odstránime (vystrihneme) jednu z jeho plôch a zvyšnú plochu natiahneme na rovinu. Získame mnohouholník (tvorený okrajmi odstránenej plochy mnohostena), rozdelený na menšie mnohouholníky (tvorené zvyšnými plochami mnohostena).
Všimnite si, že polygóny môžu byť deformované, zväčšené, zmenšené alebo dokonca zakrivené, pokiaľ na stranách nie sú žiadne medzery. Počet vrcholov, hrán a plôch sa nezmení.
Dokážme, že výsledné rozdelenie mnohouholníka na menšie mnohouholníky spĺňa rovnosť
(*)B – P + G “ = 1,
kde B je celkový počet vrcholov, P je celkový počet hrán a Г " je počet polygónov zahrnutých v oddiele. Je jasné, že Г " = Г - 1, kde Г je počet plôch danej oblasti mnohosten.
Dokážme, že rovnosť (*) sa nemení, ak je v niektorom mnohouholníku daného oddielu nakreslená uhlopriečka (obr. 5, a). Skutočne, po nakreslení takejto uhlopriečky bude mať nový oddiel B vrcholov, P+1 hrán a počet polygónov sa zvýši o jeden. Preto máme
B - (P + 1) + (G "+1) = B - P + G " .

Pomocou tejto vlastnosti nakreslíme uhlopriečky, ktoré rozdelia prichádzajúce mnohouholníky na trojuholníky a pre výsledné rozdelenie ukážeme uskutočniteľnosť rovnosti (*) (obr. 5, b). Aby sme to dosiahli, postupne odstránime vonkajšie okraje, čím sa zníži počet trojuholníkov. V tomto prípade sú možné dva prípady:
a) na odstránenie trojuholníka ABC je potrebné odstrániť dve rebrá, v našom prípade AB A B.C.;
b) na odstránenie trojuholníkaMKNje potrebné odstrániť jeden okraj, v našom prípadeMN.
V oboch prípadoch sa rovnosť (*) nezmení. Napríklad v prvom prípade po odstránení trojuholníka bude graf pozostávať z B - 1 vrcholov, P - 2 hrán a G " - 1 mnohouholníka:
(B - 1) - (P + 2) + (G " - 1) = B - P + G ".
Zvážte druhý prípad sami.
Odstránením jedného trojuholníka sa teda nezmení rovnosť (*). Pokračujúc v tomto procese odstraňovania trojuholníkov, nakoniec dospejeme k oddielu pozostávajúcom z jedného trojuholníka. Pre takéto rozdelenie platí B = 3, P = 3, Г " = 1 a teda B – Р + Г " = 1. To znamená, že rovnosť (*) platí aj pre pôvodný oddiel, z čoho nakoniec dostaneme, že pretože toto rozdelenie polygónu platí rovnosť (*). Pre pôvodný konvexný mnohosten teda platí rovnosť B - P + G = 2.
Príklad mnohostenu, pre ktorý neplatí Eulerov vzťah, znázornené na obrázku 6. Tento mnohosten má 16 vrcholov, 32 hrán a 16 plôch. Pre tento mnohosten teda platí rovnosť B – P + G = 0.
Dodatok 3.
Film Cube 2: Hypercube je sci-fi film, pokračovanie filmu Cube.
Osem cudzincov sa prebúdza v miestnostiach v tvare kocky. Izby sú umiestnené vo vnútri štvorrozmernej hyperkocky. Miestnosti sa neustále pohybujú prostredníctvom „kvantovej teleportácie“ a ak vyleziete do ďalšej miestnosti, je nepravdepodobné, že sa vrátite do predchádzajúcej. V hyperkocke sa prelínajú paralelné svety, v niektorých miestnostiach čas plynie inak a niektoré miestnosti sú pasce smrti.
Dej filmu do značnej miery opakuje dej prvého dielu, čo sa odráža aj na obrazoch niektorých postáv. V miestnostiach hyperkocky zomiera nositeľ Nobelovej ceny Rosenzweig, ktorý vypočítal presný čas zničenia hyperkocky..
Kritika
Ak sa v prvej časti ľudia uväznení v labyrinte snažili jeden druhému pomáhať, v tomto filme je to každý sám za seba. Je tu množstvo zbytočných špeciálnych efektov (alias pascí), ktoré túto časť filmu nijako logicky nespájajú s predchádzajúcou. To znamená, že sa ukazuje, že film Kocka 2 je akýmsi labyrintom budúcnosti 2020-2030, ale nie 2000. V prvej časti môže všetky typy pascí teoreticky vytvárať človek. V druhej časti sú tieto pasce akýmsi počítačovým programom, takzvanou „virtuálnou realitou“.
V geometrii hyperkocka- Toto n-rozmerná analógia štvorca ( n= 2) a kocka ( n= 3). Je to uzavretý konvexný obrazec pozostávajúci zo skupín rovnobežných čiar umiestnených na protiľahlých okrajoch obrazca a navzájom spojených v pravých uhloch.
Tento údaj je známy aj ako tesseract(tesseract). Tesseract je ku kocke ako kocka ku štvorcu. Formálnejšie možno tesseract opísať ako pravidelný konvexný štvorrozmerný polytop (polyhedron), ktorého hranica pozostáva z ôsmich kubických buniek.
Podľa Oxford English Dictionary slovo „tesseract“ vymyslel v roku 1888 Charles Howard Hinton a použil ho vo svojej knihe „A New Era of Thought“. Slovo bolo odvodené z gréckeho „τεσσερες ακτινες“ („štyri lúče“) vo forme štyroch súradnicových osí. Okrem toho sa v niektorých zdrojoch nazýval rovnaký údaj tetracube(tetracube).
n-rozmerná hyperkocka sa nazýva aj n-kocka.
Bod je hyperkocka s rozmerom 0. Ak posuniete bod o jednotku dĺžky, dostanete segment jednotkovej dĺžky - hyperkocku s rozmerom 1. Ďalej, ak posuniete segment o jednotku dĺžky v smere kolmom do smeru úsečky dostaneme kocku - hyperkocku rozmeru 2. Posunutím štvorca o jednotku dĺžky v smere kolmom na rovinu štvorca získame kocku - hyperkocku rozmeru 3. Tento proces možno zovšeobecniť na ľubovoľný počet rozmerov. Ak napríklad posuniete kocku o jednu jednotku dĺžky vo štvrtom rozmere, dostanete tesseract.
Rodina hyperkocky je jednou z mála pravidelných mnohostenov, ktoré môžu byť reprezentované v akejkoľvek dimenzii.
Prvky hyperkocky
Rozmer hyperkocka n má 2 n„strany“ (jednorozmerná čiara má 2 body; dvojrozmerný štvorec má 4 strany; trojrozmerná kocka má 6 plôch; štvorrozmerný tesseract má 8 buniek). Počet vrcholov (bodov) hyperkocky je 2 n(napríklad pre kocku - 2 3 vrcholy).
Množstvo m-rozmerné hyperkocky na hranici n-kocka sa rovná
Napríklad na hranici hyperkocky je 8 kociek, 24 štvorcov, 32 hrán a 16 vrcholov.
| n-kocka | názov | Vertex (0 tváre) |
Hrana (1 tvár) |
Hrana (2 tváre) |
Bunka (3 tváre) |
(4 tváre) | (5 tvárí) | (6-stranný) | (7 tvárí) | (8 tvárí) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-kocka | Bodka | 1 | ||||||||
| 1-kocka | Úsečka | 2 | 1 | |||||||
| 2-kocka | Námestie | 4 | 4 | 1 | ||||||
| 3-kocka | Kocka | 8 | 12 | 6 | 1 | |||||
| 4-kocka | Tesseract | 16 | 32 | 24 | 8 | 1 | ||||
| 5-kocka | Penteract | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-kocka | Hexeract | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-kocka | Hepteract | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-kocka | Octeact | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-kocka | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Projekcia do roviny
Vytvorenie hyperkocky možno znázorniť nasledujúcim spôsobom:
- Dva body A a B možno spojiť a vytvoriť úsečku AB.
- Dva paralelné segmenty AB a CD možno spojiť do štvorca ABCD.
- Dva rovnobežné štvorce ABCD a EFGH možno spojiť a vytvoriť kocku ABCDEFGH.
- Dve paralelné kocky ABCDEFGH a IJKLMNOP možno spojiť a vytvoriť tak hyperkocku ABCDEFGHIJKLMNOP.
Poslednú uvedenú štruktúru nie je ľahké vizualizovať, ale je možné zobraziť jej projekciu do dvojrozmerného alebo trojrozmerného priestoru. Navyše projekcie do dvojrozmernej roviny môžu byť užitočnejšie tým, že umožňujú preusporiadanie pozícií premietaných vrcholov. V tomto prípade je možné získať obrázky, ktoré už neodrážajú priestorové vzťahy prvkov v rámci tesseractu, ale ilustrujú štruktúru vrcholových spojení, ako v príkladoch nižšie.

Prvá ilustrácia ukazuje, ako v princípe vzniká tesseract spojením dvoch kociek. Táto schéma je podobná schéme na vytvorenie kocky z dvoch štvorcov. Druhý diagram ukazuje, že všetky okraje tesseractu majú rovnakú dĺžku. Táto schéma vás tiež núti hľadať kocky navzájom spojené. V treťom diagrame sú vrcholy tesseractu umiestnené v súlade so vzdialenosťami pozdĺž plôch vzhľadom na spodný bod. Táto schéma je zaujímavá, pretože sa používa ako základná schéma pre sieťovú topológiu spájania procesorov pri organizovaní paralelných výpočtov: vzdialenosť medzi akýmikoľvek dvoma uzlami nepresahuje 4 dĺžky hrán a existuje veľa rôznych ciest na vyrovnávanie záťaže.
Hyperkocka v umení
Hyperkocka sa objavuje v literatúre sci-fi od roku 1940, keď Robert Heinlein v príbehu „A postavil krivý dom“ opísal dom postavený v tvare tesseraktového skenu. V tomto príbehu sa tento dom zrúti a zmení sa na štvorrozmerný tesseract. Potom sa hyperkocka objavuje v mnohých knihách a poviedkach.
Film Cube 2: Hypercube je o ôsmich ľuďoch uväznených v sieti hyperkociek.
Obraz Salvadora Dalího „Ukrižovanie (Corpus Hypercubus)“, 1954, zobrazuje Ježiša ukrižovaného na skene tesseractu. Tento obraz je možné vidieť v Metropolitnom múzeu umenia v New Yorku.
Záver
Hyperkocka je jedným z najjednoduchších štvorrozmerných objektov, z ktorých je vidieť zložitosť a nevšednosť štvrtej dimenzie. A to, čo vyzerá ako nemožné v troch rozmeroch, je možné v štyroch, napríklad nemožných číslach. Takže napríklad tyče nemožného trojuholníka v štyroch rozmeroch budú spojené v pravom uhle. A toto číslo bude vyzerať takto zo všetkých uhlov pohľadu a nebude skreslené, na rozdiel od implementácií nemožného trojuholníka v trojrozmernom priestore (pozri.
Doktrína viacrozmerných priestorov sa začala objavovať v polovici 19. storočia v prácach G. Grassmanna, A. Cayleyho, B. Riemanna, W. Clifforda, L. Schläfliho a ďalších matematikov. Začiatkom 20. storočia, s príchodom teórie relativity A. Einsteina a myšlienok G. Minkowského, sa vo fyzike začal používať štvorrozmerný časopriestorový súradnicový systém.
Potom si myšlienku štvorrozmerného priestoru požičali od vedcov spisovatelia sci-fi. Vo svojich dielach rozprávali svetu o úžasných zázrakoch štvrtej dimenzie. Hrdinovia svojich diel, využívajúci vlastnosti štvorrozmerného priestoru, mohli zjesť obsah vajíčka bez poškodenia škrupiny a vypiť nápoj bez toho, aby otvorili uzáver fľaše. Zlodeji odstránili poklad z trezoru cez štvrtú dimenziu. Články reťaze sa dajú ľahko odpojiť a uzol na lane je možné rozviazať bez toho, aby ste sa dotkli jeho koncov. Chirurgovia vykonávali operácie vnútorných orgánov bez toho, aby pacientovi rezali telesné tkanivo. Mystici umiestnili duše zosnulých do štvrtej dimenzie. Pre bežného človeka zostala myšlienka štvorrozmerného priestoru nepochopiteľná a tajomná a mnohí vo všeobecnosti považujú štvorrozmerný priestor za výplod fantázie vedcov a autorov sci-fi, ktorý nemá nič spoločné s realitou.
Problém vnímania
Tradične sa verí, že človek nemôže vnímať a predstavovať si štvorrozmerné postavy, keďže je trojrozmernou bytosťou. Subjekt vníma trojrozmerné postavy pomocou sietnice, ktorá je dvojrozmerná. Na vnímanie štvorrozmerných postáv je potrebná trojrozmerná sietnica, ale ľudia túto schopnosť nemajú.
Aby sme získali jasnú predstavu o štvorrozmerných obrazcoch, použijeme analógie z menejrozmerných priestorov na extrapoláciu na vyššierozmerné obrazce, použijeme metódu modelovania a použijeme metódy systémovej analýzy na hľadanie vzorov medzi prvkami štvorrozmerného systému. rozmerné postavy. Navrhované modely musia dostatočne popisovať vlastnosti štvorrozmerných útvarov, nesmú si navzájom odporovať a dostatočne porozumieť štvorrozmernému útvaru a predovšetkým jeho geometrickému tvaru. Keďže v literatúre neexistuje systematický a vizuálny popis štvorrozmerných postáv, ale iba ich názvy označujúce niektoré vlastnosti, navrhujeme začať štúdium štvorrozmerných postáv najjednoduchším - štvorrozmernou kockou, ktorá sa nazýva hyperkocka.
Definícia hyperkocky
Hyperkockaje pravidelný polytop, ktorého bunkou je kocka.
Polytope je štvorrozmerný obrazec, ktorého hranicu tvoria mnohosteny. Analógom polytopovej bunky je tvár mnohostenu. Hyperkocka je analógom trojrozmernej kocky.
Budeme mať predstavu o hyperkocke, ak poznáme jej vlastnosti. Subjekt vníma určitý objekt a predstavuje ho vo forme určitého modelu. Využime túto metódu a predstavme myšlienku hyperkocky vo forme rôznych modelov.
Analytický model
Jednorozmerný priestor (priamku) budeme považovať za usporiadanú množinu bodovM(X), Kde X– súradnica ľubovoľného bodu na priamke. Potom je segment jednotky špecifikovaný zadaním dvoch bodov:A(0) a B(1).
Rovina (dvojrozmerný priestor) môže byť považovaná za usporiadanú množinu bodov M(X; r). Jednotkový štvorec bude úplne definovaný svojimi štyrmi vrcholmi: A(0; 0), B(1; 0), C(1; 1), D(0; 1). Súradnice vrcholov štvorca sa získajú pridaním nuly a potom jednotky k súradniciam segmentu.
Trojrozmerný priestor - usporiadaná množina bodov M(X; r; z). Na definovanie trojrozmernej kocky je potrebných osem bodov:
A(0; 0; 0), B(1; 0; 0), C(1; 1; 0), D(0; 1; 0),
E(0; 0; 1), F(1; 0; 1), G(1; 1; 1), H(0; 1; 1).
Súradnice kocky získame zo súradníc štvorca pridaním nuly a potom jednotky.
Štvorrozmerný priestor je usporiadaná množina bodov M(X; r; z; t). Ak chcete definovať hyperkocku, musíte určiť súradnice jej šestnástich vrcholov:
A(0; 0; 0; 0), B(1; 0; 0; 0), C(1; 1; 0; 0), D(0; 1; 0; 0),
E(0; 0; 1; 0), F(1; 0; 1; 0), G(1; 1; 1; 0), H(0; 1; 1; 0),
K(0; 0; 0; 1), L(1; 0; 0; 1), M(1; 1; 0; 1), N(0; 1; 0; 1),
O(0; 0; 1; 1), P(1; 0; 1; 1), R(1; 1; 1; 1), S(0; 1; 1; 1).
Súradnice hyperkocky sa získajú zo súradníc trojrozmernej kocky pridaním štvrtej súradnice rovnej nule a potom jednej.
Pomocou vzorcov analytickej geometrie pre štvorrozmerný euklidovský priestor je možné získať vlastnosti hyperkocky.
Ako príklad zvážte výpočet dĺžky hlavnej uhlopriečky hyperkocky. Predpokladajme, že potrebujeme nájsť vzdialenosť medzi bodmi A(0, 0, 0, 0) a R(1, 1, 1, 1). Na to použijeme vzorec vzdialenosti v štvorrozmernom euklidovskom priestore.
V dvojrozmernom priestore (v rovine) vzdialenosť medzi bodmi A(X 1 , r 1) a B(X 2 , r 2) vypočítané podľa vzorca
Tento vzorec vyplýva z Pytagorovej vety.
Zodpovedajúci vzorec pre vzdialenosť medzi bodmi A(X 1 , r 1 , z 1) a B(X 2 , r 2 , z 2) v trojrozmernom priestore má tvar
A v jednorozmernom priestore (na priamke) medzi bodmi A( X 1) a B( X 2) môžete napísať zodpovedajúci vzorec vzdialenosti:
Podobne aj vzdialenosť medzi bodmi A(X 1 , r 1 , z 1 , t 1) a B(X 2 , r 2 , z 2 , t 2) v štvorrozmernom priestore sa vypočíta podľa vzorca:
Pre navrhovaný príklad nájdeme
Hyperkocka teda existuje analyticky a jej vlastnosti nemožno opísať horšie ako vlastnosti trojrozmernej kocky.
Dynamický model
Analytický model hyperkocky je veľmi abstraktný, preto uvažujme o inom modeli – o dynamickom.
Bod (nulový obrazec), pohybujúci sa v jednom smere, generuje segment (jednorozmerný obrazec). Segment, ktorý sa pohybuje v smere kolmom na seba, vytvára štvorec (dvojrozmerný obrazec). Štvorec, ktorý sa pohybuje v smere kolmom na rovinu štvorca, vytvára kocku (trojrozmerný obrazec).
Kocka, ktorá sa pohybuje kolmo na trojrozmerný priestor, v ktorom sa pôvodne nachádzala, vytvára hyperkocku (štvorrozmernú postavu).
Hranica hyperkocky je trojrozmerná, konečná a uzavretá. Pozostáva z trojrozmernej kocky v počiatočnej polohe, trojrozmernej kocky v konečnej polohe a šiestich kociek vytvorených pohybom štvorcov pôvodnej kocky v smere štvrtého rozmeru. Celá hranica hyperkocky pozostáva z 8 trojrozmerných kociek (buniek).
Pri pohybe v počiatočnej polohe mala kocka 8 vrcholov a v konečnej polohe bolo tiež 8 vrcholov. Preto má hyperkocka spolu 16 vrcholov.
Z každého vrcholu vychádzajú štyri vzájomne kolmé hrany. Hyperkocka má hrán celkom 32. Vo svojej počiatočnej polohe mala 12 hrán, v konečnej polohe bolo hrán tiež 12 a 8 hrán tvorilo vrcholy kocky pri pohybe v štvrtom rozmere.
Hranicu hyperkocky teda tvorí 8 kociek, ktoré pozostávajú z 24 štvorcov. Konkrétne 6 štvorcov v počiatočnej polohe, 6 v konečnej polohe a 12 štvorcov vytvorených posunutím 12 hrán v smere štvrtého rozmeru.
Geometrický model
Dynamický model hyperkocky sa nemusí zdať dostatočne jasný. Zvážte preto geometrický model hyperkocky. Ako získame geometrický model 3D kocky? Urobíme z toho vývoj a z vývoja „zlepíme“ model kocky. Rozvinutie trojrozmernej kocky pozostáva zo štvorca, ku ktorého stranám je pripevnený štvorec plus ďalší štvorec.  Otáčame susedné štvorce okolo strán štvorca, a spájame susedné strany štvorcov k sebe. A zvyšné štyri strany uzavrieme posledným štvorcom (obr. 1).
Otáčame susedné štvorce okolo strán štvorca, a spájame susedné strany štvorcov k sebe. A zvyšné štyri strany uzavrieme posledným štvorcom (obr. 1).
Uvažujme podobne aj o vývoji hyperkocky. Jeho vývoj bude trojrozmerná figúrka pozostávajúca z pôvodnej trojrozmernej kocky, šiestich kociek susediacich s každou plochou pôvodnej kocky a jednej ďalšej kocky. Trojrozmerných kociek je celkovo osem (obr. 2). Ak chcete získať štvorrozmernú kocku (hyperkocku) z tohto vývoja, musíte otočiť každú zo susedných kociek o 90 stupňov. Tieto susedné kocky budú umiestnené v inom trojrozmernom priestore. Spojte susedné plochy (štvorce) kociek k sebe. Umiestnite ôsmu kocku s jej tvárami na zostávajúce prázdne miesto. Dostaneme štvorrozmernú postavu – hyperkocku, ktorej hranicu tvorí osem trojrozmerných kociek.
Obrázok hyperkocky
 Vyššie bolo ukázané, ako „zlepiť“ model hyperkocky z trojrozmerného skenovania. Obrazy získavame pomocou projekcie. Stredový priemet trojrozmernej kocky (jej obraz do roviny) vyzerá takto (obr. 3). Vo vnútri štvorca je ďalší štvorec. Zodpovedajúce vrcholy štvorca sú spojené segmentmi. Priľahlé štvorce sú zobrazené ako lichobežníky, hoci v trojrozmernom priestore sú štvorcami. Vnútorné a vonkajšie štvorce sú rôzne veľké, ale v reálnom trojrozmernom priestore sú to rovnaké štvorce.
Vyššie bolo ukázané, ako „zlepiť“ model hyperkocky z trojrozmerného skenovania. Obrazy získavame pomocou projekcie. Stredový priemet trojrozmernej kocky (jej obraz do roviny) vyzerá takto (obr. 3). Vo vnútri štvorca je ďalší štvorec. Zodpovedajúce vrcholy štvorca sú spojené segmentmi. Priľahlé štvorce sú zobrazené ako lichobežníky, hoci v trojrozmernom priestore sú štvorcami. Vnútorné a vonkajšie štvorce sú rôzne veľké, ale v reálnom trojrozmernom priestore sú to rovnaké štvorce.
 Podobne centrálna projekcia štvorrozmernej kocky do trojrozmerného priestoru bude vyzerať takto: vo vnútri jednej kocky je ďalšia kocka. Zodpovedajúce vrcholy kociek sú spojené segmentmi. Vnútorná a vonkajšia kocka majú v trojrozmernom priestore rozdielne veľkosti, no v štvorrozmernom priestore sú to rovnaké kocky (obr. 4).
Podobne centrálna projekcia štvorrozmernej kocky do trojrozmerného priestoru bude vyzerať takto: vo vnútri jednej kocky je ďalšia kocka. Zodpovedajúce vrcholy kociek sú spojené segmentmi. Vnútorná a vonkajšia kocka majú v trojrozmernom priestore rozdielne veľkosti, no v štvorrozmernom priestore sú to rovnaké kocky (obr. 4).
Šesť zrezaných ihlanov sú obrazy rovnakých šiestich buniek (kociek) štvorrozmernej kocky.
Túto trojrozmernú projekciu je možné nakresliť na rovinu a overiť, že vlastnosti hyperkocky získané pomocou dynamického modelu sú pravdivé.
Hyperkocka má 16 vrcholov, 32 hrán, 24 plôch (štvorcov), 8 buniek (kociek). Z každého vrcholu vychádzajú štyri vzájomne kolmé hrany. Hranica hyperkocky je trojrozmerný uzavretý konvexný útvar, ktorého objem (bočný objem hyperkocky) sa rovná ôsmim jednotkovým trojrozmerným kockám. Tento obrazec vo svojom vnútri obsahuje jednotkovú hyperkocku, ktorej hyperobjem sa rovná hyperobjemu jednotkovej hyperkocky.
Záver
Cieľom tejto práce bolo poskytnúť úvodný úvod do štvorrozmerného priestoru. Urobilo sa to pomocou príkladu najjednoduchšej postavy - hyperkocky.
Svet štvorrozmerného priestoru je úžasný! V ňom sú spolu s podobnými postavami v trojrozmernom priestore aj postavy, ktoré v trojrozmernom priestore nemajú obdobu.
Mnohé javy hmotného sveta, makrosveta a megasveta, napriek obrovským úspechom vo fyzike, chémii a astronómii, zostali nevysvetlené.
Neexistuje jediná teória, ktorá by vysvetľovala všetky sily prírody. Neexistuje žiadny uspokojivý model vesmíru, ktorý by vysvetľoval jeho štruktúru a vylučoval paradoxy.
Po oboznámení sa s vlastnosťami štvorrozmerného priestoru a požičaním si niektorých myšlienok zo štvorrozmernej geometrie bude možné nielen vytvárať prísnejšie teórie a modely hmotného sveta, ale aj vytvárať nástroje a systémy, ktoré fungujú podľa zákonov. štvorrozmerného sveta, potom budú ľudské schopnosti ešte pôsobivejšie.
Bakalyar Maria
Študujú sa metódy na zavedenie konceptu štvorrozmernej kocky (tesseract), jej štruktúra a niektoré vlastnosti. Otázka, aké trojrozmerné objekty sa získajú, keď štvorrozmernú kocku pretínajú nadroviny rovnobežné s jej trojrozmernými plochami , ako aj nadroviny kolmé na jeho hlavnú uhlopriečku. Uvažuje sa s prístrojom viacrozmernej analytickej geometrie používaným na výskum.
Stiahnuť ▼:
Náhľad:
Úvod……………………………………………………………………………………………….2
Hlavná časť………………………………………………………………………..4
Závery………….. ………………………………………………………………..12
Referencie………………………………………………………………..13
Úvod
Štvorrozmerný priestor už dlho priťahuje pozornosť profesionálnych matematikov aj ľudí, ktorí majú ďaleko od štúdia tejto vedy. Záujem o štvrtú dimenziu môže byť spôsobený predpokladom, že náš trojrozmerný svet je „ponorený“ do štvorrozmerného priestoru, tak ako je rovina „ponorená“ do trojrozmerného priestoru, priama čiara je „ponorená“ do rovine a bod je v priamke. Okrem toho štvorrozmerný priestor zohráva dôležitú úlohu v modernej teórii relativity (tzv. časopriestorový alebo Minkowského priestor) a možno ho tiež považovať za špeciálny prípad.dimenzionálny euklidovský priestor (s).
Štvorrozmerná kocka (tesseract) je objekt v štvorrozmernom priestore, ktorý má maximálny možný rozmer (rovnako ako obyčajná kocka je objekt v trojrozmernom priestore). Všimnite si, že je to aj priamy záujem, konkrétne sa môže objaviť v optimalizačných problémoch lineárneho programovania (ako oblasť, v ktorej sa nachádza minimum alebo maximum lineárnej funkcie štyroch premenných) a používa sa aj v digitálnej mikroelektronike (keď programovanie činnosti displeja elektronických hodiniek). Okrem toho samotný proces štúdia štvorrozmernej kocky prispieva k rozvoju priestorového myslenia a predstavivosti.
V dôsledku toho je štúdium štruktúry a špecifických vlastností štvorrozmernej kocky celkom relevantné. Stojí za zmienku, že z hľadiska štruktúry bola štvorrozmerná kocka celkom dobre študovaná. Oveľa zaujímavejší je charakter jeho sekcií rôznymi nadrovinami. Hlavným cieľom tejto práce je teda študovať štruktúru tesseractu, ako aj objasniť otázku, aké trojrozmerné objekty sa získajú, ak sa štvorrozmerná kocka rozčlení nadrovinami rovnobežnými s jednou z jej trojrozmerných kociek. rozmernými plochami alebo nadrovinami kolmými na jeho hlavnú uhlopriečku. Nadrovinu v štvorrozmernom priestore budeme nazývať trojrozmerný podpriestor. Môžeme povedať, že priamka na rovine je jednorozmerná nadrovina, rovina v trojrozmernom priestore je dvojrozmerná nadrovina.
Cieľ určil ciele štúdie:
1) Študovať základné fakty viacrozmernej analytickej geometrie;
2) Preštudujte si vlastnosti konštrukcie kociek s rozmermi od 0 do 3;
3) Preštudujte si štruktúru štvorrozmernej kocky;
4) Analyticky a geometricky opíšte štvorrozmernú kocku;
5) Vytvorte modely vývoja a stredové projekcie trojrozmerných a štvorrozmerných kociek.
6) Pomocou prístroja viacrozmernej analytickej geometrie opíšte trojrozmerné objekty, ktoré sú výsledkom priesečníka štvorrozmernej kocky s nadrovinami rovnobežnými s jednou z jej trojrozmerných stien alebo nadrovinami kolmými na jej hlavnú uhlopriečku.
Takto získané informácie nám umožnia lepšie pochopiť štruktúru tesseractu, ako aj identifikovať hlboké analógie v štruktúre a vlastnostiach kociek rôznych rozmerov.
Hlavná časť
Najprv popíšeme matematický aparát, ktorý budeme počas tejto štúdie používať.
1) Súradnice vektora: ak, To
2) Rovnica nadroviny s normálovým vektorom vyzerá ako Tu
3) Lietadlá a sú paralelné vtedy a len vtedy
4) Vzdialenosť medzi dvoma bodmi sa určí takto: ak, To
5) Podmienka pre ortogonalitu vektorov:
Najprv si povedzme, ako opísať štvorrozmernú kocku. Dá sa to urobiť dvoma spôsobmi - geometrickým a analytickým.
Ak hovoríme o geometrickej metóde špecifikácie, potom je vhodné sledovať proces konštrukcie kociek, počnúc nulovým rozmerom. Kocka nulového rozmeru je bod (mimochodom, bod môže hrať aj úlohu gule nulového rozmeru). Ďalej zavedieme prvý rozmer (os x) a na zodpovedajúcej osi označíme dva body (dve kocky s nulovým rozmerom) umiestnené vo vzdialenosti 1 od seba. Výsledkom je segment - jednorozmerná kocka. Hneď si všimnime charakteristický znak: Hranica (konce) jednorozmernej kocky (segmentu) sú dve nulové kocky (dva body). Ďalej zavedieme druhý rozmer (ordinátna os) a na rovineZostrojme dve jednorozmerné kocky (dva segmenty), ktorých konce sú od seba vzdialené 1 (v skutočnosti je jeden zo segmentov ortogonálnym priemetom druhého). Spojením zodpovedajúcich koncov segmentov získame štvorec - dvojrozmernú kocku. Opäť si všimnite, že hranicou dvojrozmernej kocky (štvorca) sú štyri jednorozmerné kocky (štyri segmenty). Nakoniec zavedieme tretiu dimenziu (aplikovanú os) a zostrojíme v priestoredva štvorce tak, že jeden z nich je kolmým priemetom druhého (zodpovedajúce vrcholy štvorcov sú od seba vzdialené 1). Spojme zodpovedajúce vrcholy so segmentmi - dostaneme trojrozmernú kocku. Vidíme, že hranicou trojrozmernej kocky je šesť dvojrozmerných kociek (šesť štvorcov). Opísané konštrukcie nám umožňujú identifikovať nasledujúci vzor: v každom krokurozmerná kocka sa „pohybuje a zanecháva stopu“.e meranie vo vzdialenosti 1, pričom smer pohybu je kolmý na kocku. Práve formálne pokračovanie tohto procesu nám umožňuje dospieť ku konceptu štvorrozmernej kocky. Totiž, prinútime trojrozmernú kocku, aby sa posunula v smere štvrtého rozmeru (kolmo na kocku) o vzdialenosť 1. Postupujeme podobne ako v predchádzajúcom, teda spojením zodpovedajúcich vrcholov kociek, získame štvorrozmernú kocku. Treba si uvedomiť, že geometricky je takáto konštrukcia v našom priestore nemožná (keďže je trojrozmerný), ale tu sa z logického hľadiska nestretávame s rozpormi. Teraz prejdime k analytickému popisu štvorrozmernej kocky. Získava sa aj formálne pomocou analógie. Takže analytická špecifikácia kocky s nulovými rozmermi má tvar:
Analytická úloha jednorozmernej jednotkovej kocky má tvar:
Analytická úloha dvojrozmernej jednotkovej kocky má tvar:
Analytická úloha trojrozmernej jednotkovej kocky má tvar:
Teraz je veľmi ľahké poskytnúť analytickú reprezentáciu štvorrozmernej kocky, konkrétne:
Ako vidíme, geometrické aj analytické metódy definovania štvorrozmernej kocky využívali metódu analógií.
Teraz pomocou prístroja analytickej geometrie zistíme, aká je štruktúra štvorrozmernej kocky. Po prvé, poďme zistiť, aké prvky obsahuje. Aj tu môžeme použiť analógiu (na predloženie hypotézy). Hranicami jednorozmernej kocky sú body (nulové kocky), dvojrozmernej kocky - segmenty (jednorozmerné kocky), trojrozmernej kocky - štvorce (dvojrozmerné plochy). Dá sa predpokladať, že hranice tesseractu sú trojrozmerné kocky. Aby sme to dokázali, objasnime, čo sa myslí pod pojmom vrcholy, hrany a plochy. Vrcholy kocky sú jej rohové body. To znamená, že súradnice vrcholov môžu byť nuly alebo jednotky. Odhalí sa teda súvislosť medzi rozmerom kocky a počtom jej vrcholov. Použime kombinatorické pravidlo súčinu - od vrcholumeraná kocka má presnesúradnice, z ktorých každá sa rovná nule alebo jednotke (nezávisle od všetkých ostatných), potom celkovo existujevrcholov Pre každý vrchol sú teda všetky súradnice pevné a môžu sa rovnať alebo . Ak opravíme všetky súradnice (všetky súradnice budú rovnaké alebo , bez ohľadu na ostatné), okrem jednej získame rovné čiary obsahujúce hrany kocky. Podobne ako v predchádzajúcej, môžete spočítať, že existujú presneveci. A ak teraz opravíme všetky súradnice (všetky súradnice budú rovnaké alebo , bez ohľadu na ostatné), okrem niektorých dvoch získame roviny obsahujúce dvojrozmerné plochy kocky. Pomocou pravidla kombinatoriky zistíme, že existujú presneveci. Ďalej, podobne - stanovenie všetkých súradníc (rovnanie každej z nich alebo , nezávisle od ostatných), okrem niektorých troch získame nadroviny obsahujúce trojrozmerné steny kocky. Pomocou rovnakého pravidla vypočítame ich počet - presneatď. Pre náš výskum to bude stačiť. Aplikujme získané výsledky na štruktúru štvorrozmernej kocky, a to vo všetkých odvodených vzorcoch, ktoré vložíme. Štvorrozmerná kocka má teda: 16 vrcholov, 32 hrán, 24 dvojrozmerných plôch a 8 trojrozmerných plôch. Pre prehľadnosť definujme analyticky všetky jeho prvky.
Vrcholy štvorrozmernej kocky:
Hrany štvorrozmernej kocky ():
Dvojrozmerné plochy štvorrozmernej kocky (podobné obmedzenia):
Trojrozmerné plochy štvorrozmernej kocky (podobné obmedzenia):
Teraz, keď bola štruktúra štvorrozmernej kocky a spôsoby jej definovania dostatočne podrobne opísané, pristúpme k realizácii hlavného cieľa - objasniť povahu rôznych častí kocky. Začnime s elementárnym prípadom, keď sú rezy kocky rovnobežné s jednou z jej trojrozmerných stien. Zvážte napríklad jeho časti s nadrovinami rovnobežnými s tvárouZ analytickej geometrie je známe, že každý takýto úsek bude daný rovnicouAnalyticky definujme príslušné sekcie:
Ako vidíme, získali sme analytickú špecifikáciu pre trojrozmernú jednotkovú kocku ležiacu v nadrovine
Aby sme vytvorili analógiu, napíšme rez trojrozmernej kocky rovinou Dostaneme:
Toto je štvorec ležiaci v rovine. Analógia je zrejmá.
Rezy štvorrozmernej kocky nadrovinamidať úplne podobné výsledky. Pôjde tiež o jednotlivé trojrozmerné kocky ležiace v nadrovinách resp.
Teraz uvažujme rezy štvorrozmernej kocky s nadrovinami kolmými na jej hlavnú uhlopriečku. Najprv vyriešme tento problém pre trojrozmernú kocku. Použitím vyššie opísanej metódy definovania jednotkovej trojrozmernej kocky prichádza k záveru, že za hlavnú uhlopriečku môže brať napríklad úsečka s koncami A . To znamená, že vektor hlavnej uhlopriečky bude mať súradnice. Preto rovnica akejkoľvek roviny kolmej na hlavnú uhlopriečku bude:
Poďme určiť hranice zmeny parametrov. Pretože , potom pridaním týchto nerovností po členoch dostaneme:
Alebo .
Ak potom (kvôli obmedzeniam). Rovnako - ak, To . Takže kedy a kedy rovina rezu a kocka majú presne jeden spoločný bod ( A v uvedenom poradí). Teraz si všimnime nasledovné. Ak(opäť kvôli variabilným obmedzeniam). Zodpovedajúce roviny pretínajú tri plochy naraz, pretože inak by bola rovina rezu rovnobežná s jednou z nich, čo sa nedeje podľa podmienky. Ak, potom rovina pretína všetky steny kocky. Ak, potom rovina pretína steny. Uvedieme zodpovedajúce výpočty.
Nechaj Potom lietadloprekračuje hranicu v priamej línii a . Navyše okraj. Hrana rovina sa pretína v priamke, a
Nechaj Potom lietadloprekračuje hranicu:
okraj v priamke a .
okraj v priamke a .
okraj v priamke a .
okraj v priamke a .
okraj v priamke a .
okraj v priamke a .
Tentoraz dostaneme šesť segmentov, ktoré majú postupne spoločné konce:
Nechaj Potom lietadloprekračuje hranicu v priamej línii a . Hrana rovina sa pretína v priamke a . Hrana rovina sa pretína v priamke, a . To znamená, že dostaneme tri segmenty, ktoré majú párovo spoločné konce:Teda pre zadané hodnoty parametrovrovina bude pretínať kocku pozdĺž pravidelného trojuholníka s vrcholmi
Takže tu je komplexný popis rovinných útvarov získaných, keď kocku pretína rovina kolmá na jej hlavnú uhlopriečku. Hlavná myšlienka bola nasledovná. Je potrebné pochopiť, ktoré steny sa rovina pretína, pozdĺž ktorých množín ich pretína a ako tieto množiny navzájom súvisia. Napríklad, ak sa ukázalo, že rovina pretína presne tri steny pozdĺž segmentov, ktoré majú párovo spoločné konce, potom je tento úsek rovnostranný trojuholník (čo je dokázané priamym výpočtom dĺžok segmentov), ktorého vrcholy sú tieto konce segmentov.
Pomocou toho istého prístroja a rovnakej myšlienky štúdia sekcií možno úplne analogicky vyvodiť nasledujúce skutočnosti:
1) Vektor jednej z hlavných uhlopriečok štvorrozmernej jednotkovej kocky má súradnice
2) Akákoľvek nadrovina kolmá na hlavnú uhlopriečku štvorrozmernej kocky môže byť napísaná v tvare.
3) V rovnici sečnej nadroviny parametersa môže meniť od 0 do 4;
4) Kedy a sečenská nadrovina a štvorrozmerná kocka majú jeden spoločný bod ( A v uvedenom poradí);
5) Kedy prierez vytvorí pravidelný štvorsten;
6) Kedy v priereze bude výsledkom osemsten;
7) Kedy prierez vytvorí pravidelný štvorsten.
V súlade s tým tu nadrovina pretína tesseract pozdĺž roviny, na ktorej sa v dôsledku obmedzení premenných rozlišuje trojuholníková oblasť (analógia - rovina pretínala kocku pozdĺž priamky, na ktorej v dôsledku obmedzení premenných premenných, bol rozlíšený segment). V prípade 5) nadrovina pretína presne štyri trojrozmerné plochy tesseractu, to znamená, že sa získajú štyri trojuholníky, ktoré majú párovo spoločné strany, inými slovami, tvoria štvorsten (ako to možno vypočítať, je správne). V prípade 6) nadrovina pretína presne osem trojrozmerných plôch tesseraktu, to znamená, že sa získa osem trojuholníkov, ktoré majú postupne spoločné strany, inými slovami, tvoria oktaedrón. Prípad 7) je úplne podobný prípadu 5).
Ukážme si to na konkrétnom príklade. Konkrétne študujeme rez štvorrozmernou kockou nadrovinouKvôli premenlivým obmedzeniam táto nadrovina pretína nasledujúce trojrozmerné plochy: Hrana pretína pozdĺž rovinyKvôli obmedzeniam premenných máme:Dostaneme trojuholníkovú oblasť s vrcholmiďalejdostaneme trojuholníkKeď nadrovina pretína tvárdostaneme trojuholníkKeď nadrovina pretína tvárdostaneme trojuholníkTakže vrcholy štvorstenu majú nasledujúce súradnice. Ako sa dá ľahko vypočítať, tento štvorsten je skutočne pravidelný.
závery
V procese tohto výskumu sa teda študovali základné fakty viacrozmernej analytickej geometrie, študovali sa vlastnosti konštrukcie kociek s rozmermi od 0 do 3, študovala sa štruktúra štvorrozmernej kocky, štvorrozmerná kocka analyticky a geometricky boli popísané modely vývoja a stredové projekcie trojrozmerných a štvorrozmerných kociek, trojrozmerné kocky boli analyticky popísané objekty, ktoré vznikli priesečníkom štvorrozmernej kocky s nadrovinami rovnobežnými s jednou z jej trojrozmerných kociek. rozmernými plochami alebo s nadrovinami kolmými na jeho hlavnú uhlopriečku.
Uskutočnený výskum umožnil identifikovať hlboké analógie v štruktúre a vlastnostiach kociek rôznych rozmerov. Použitá analogická technika môže byť použitá vo výskume, napr.rozmerová guľa resprozmerový simplex. menoviterozmernú guľu možno definovať ako množinu bodovrozmerný priestor rovnako vzdialený od daného bodu, ktorý sa nazýva stred gule. ďalejrozmerový simplex možno definovať ako časťrozmerový priestor obmedzený minimálnym počtomrozmerové nadroviny. Napríklad jednorozmerný simplex je úsečka (časť jednorozmerného priestoru ohraničená dvoma bodmi), dvojrozmerný simplex je trojuholník (časť dvojrozmerného priestoru ohraničená tromi čiarami), trojrozmerný simplex je štvorsten (časť trojrozmerného priestoru, ohraničená štyrmi rovinami). nakoniecako súčiastku definujeme rozmerový simplexrozmerový priestor, obmedzenýnadrovina dimenzie.
Všimnite si, že napriek početným aplikáciám tesseractu v niektorých oblastiach vedy je tento výskum stále prevažne matematickou štúdiou.
Bibliografia
1) Bugrov Ya.S., Nikolsky S.M.Vyššia matematika, zväzok 1 – M.: Drop, 2005 – 284 s.
2) Kvantové. Štvorrozmerná kocka / Duzhin S., Rubtsov V., č. 6, 1986.
3) Kvantové. Ako kresliť rozmerná kocka / Demidovich N.B., č. 8, 1974.









