ლოგარითმების მაგალითები წილადი ფუძეებით. ბუნებრივი ლოგარითმი, ფუნქცია ln x

ინსტრუქციები

დაწერეთ მოცემული ლოგარითმული გამოხატულება. თუ გამოთქმა იყენებს 10-ის ლოგარითმს, მაშინ მისი აღნიშვნა მცირდება და ასე გამოიყურება: lg b არის ათობითი ლოგარითმი. თუ ლოგარითმს საფუძვლად აქვს რიცხვი e, ჩაწერეთ გამოთქმა: ln b – ბუნებრივი ლოგარითმი. გასაგებია, რომ ნებისმიერის შედეგი არის ძალა, რომელზედაც უნდა გაიზარდოს საბაზისო რიცხვი, რომ მივიღოთ b რიცხვი.

ორი ფუნქციის ჯამის პოვნისას თქვენ უბრალოდ უნდა განასხვავოთ ისინი სათითაოდ და დაამატოთ შედეგები: (u+v)" = u"+v";

ორი ფუნქციის ნამრავლის წარმოებულის პოვნისას აუცილებელია პირველი ფუნქციის წარმოებული გავამრავლოთ მეორეზე და დავამატოთ მეორე ფუნქციის წარმოებული გამრავლებული პირველ ფუნქციაზე: (u*v)" = u"*v. +v"*u;

ორი ფუნქციის კოეფიციენტის წარმოებული რომ ვიპოვოთ, საჭიროა დივიდენდის წარმოებულის ნამრავლს გამრავლებულ ფუნქციაზე გამოვაკლოთ გამყოფის წარმოებულის ნამრავლი გამრავლებული დივიდენდის ფუნქციაზე და გავყოთ. ეს ყველაფერი გამყოფი ფუნქციის კვადრატში. (u/v)" = (u"*v-v"*u)/v^2;

თუ რთული ფუნქციაა მოცემული, მაშინ აუცილებელია შიდა ფუნქციის წარმოებულის და გარეგანის წარმოებულის გამრავლება. მოდით y=u(v(x)), შემდეგ y"(x)=y"(u)*v"(x).

ზემოთ მიღებული შედეგების გამოყენებით, შეგიძლიათ განასხვავოთ თითქმის ნებისმიერი ფუნქცია. ასე რომ, მოდით შევხედოთ რამდენიმე მაგალითს:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *x));
ასევე არის პრობლემები წარმოებულის გამოთვლასთან დაკავშირებით. მოცემული იყოს ფუნქცია y=e^(x^2+6x+5), თქვენ უნდა იპოვოთ ფუნქციის მნიშვნელობა x=1 წერტილში.
1) იპოვეთ ფუნქციის წარმოებული: y"=e^(x^2-6x+5)*(2*x +6).

2) გამოთვალეთ ფუნქციის მნიშვნელობა მოცემულ წერტილში y"(1)=8*e^0=8

ვიდეო თემაზე

სასარგებლო რჩევა

ისწავლეთ ელემენტარული წარმოებულების ცხრილი. ეს მნიშვნელოვნად დაზოგავს დროს.

წყაროები:

• მუდმივის წარმოებული

მაშ, რა განსხვავებაა ირაციონალურ განტოლებასა და რაციონალურ განტოლებას შორის? თუ უცნობი ცვლადი არის კვადრატული ფესვის ნიშნის ქვეშ, მაშინ განტოლება ითვლება ირაციონალურად.

ინსტრუქციები

ასეთი განტოლებების ამოხსნის მთავარი მეთოდია ორივე მხარის აგების მეთოდი განტოლებებიმოედანზე. თუმცა. ეს ბუნებრივია, პირველი რაც უნდა გააკეთოთ არის ნიშნის მოშორება. ეს მეთოდი არ არის ტექნიკურად რთული, მაგრამ ზოგჯერ შეიძლება გამოიწვიოს პრობლემები. მაგალითად, განტოლება არის v(2x-5)=v(4x-7). ორივე მხარის კვადრატში მიიღებთ 2x-5=4x-7. ასეთი განტოლების ამოხსნა არ არის რთული; x=1. მაგრამ ნომერი 1 არ იქნება მოცემული განტოლებები. რატომ? შეცვალეთ ერთი განტოლებაში x-ის მნიშვნელობის ნაცვლად და მარჯვენა და მარცხენა მხარეები შეიცავს გამონათქვამებს, რომლებსაც აზრი არ აქვს, ანუ. ეს მნიშვნელობა არ არის მოქმედი კვადრატული ფესვისთვის. მაშასადამე, 1 არის უცხო ფესვი და, შესაბამისად, ამ განტოლებას ფესვები არ აქვს.

ასე რომ, ირაციონალური განტოლება წყდება მისი ორივე მხარის კვადრატის მეთოდის გამოყენებით. და განტოლების ამოხსნის შემდეგ, აუცილებელია ზედმეტი ფესვების ამოჭრა. ამისათვის შეცვალეთ ნაპოვნი ფესვები თავდაპირველ განტოლებაში.

განიხილეთ კიდევ ერთი.
2х+vх-3=0
რა თქმა უნდა, ეს განტოლება შეიძლება ამოხსნას იმავე განტოლების გამოყენებით, როგორც წინა. ნაერთების გადატანა განტოლებები, რომლებსაც არ აქვთ კვადრატული ფესვი, მარჯვნივ და შემდეგ გამოიყენეთ კვადრატის მეთოდი. ამოხსნათ მიღებული რაციონალური განტოლება და ფესვები. მაგრამ ასევე სხვა, უფრო ელეგანტური. შეიყვანეთ ახალი ცვლადი; vх=y. შესაბამისად მიიღებთ 2y2+y-3=0 ფორმის განტოლებას. ანუ ჩვეულებრივი კვადრატული განტოლება. იპოვნეთ მისი ფესვები; y1=1 და y2=-3/2. შემდეგი, გადაწყვიტეთ ორი განტოლებები vх=1; vх=-3/2. მეორე განტოლებას არ აქვს ფესვები, პირველიდან ვხვდებით, რომ x=1. არ დაგავიწყდეთ ფესვების შემოწმება.

პირადობის ამოხსნა საკმაოდ მარტივია. ამისათვის საჭიროა იდენტური გარდაქმნების განხორციელება დასახული მიზნის მიღწევამდე. ამრიგად, მარტივი არითმეტიკული ოპერაციების დახმარებით, დასმული პრობლემა მოგვარდება.

დაგჭირდებათ

• - ქაღალდი;
• -კალამი.

ინსტრუქციები

ასეთი გარდაქმნებიდან უმარტივესი არის ალგებრული შემოკლებული გამრავლება (როგორიცაა ჯამის კვადრატი (განსხვავება), კვადრატების სხვაობა, ჯამი (განსხვავება), ჯამის კუბი (განსხვავება)). გარდა ამისა, არსებობს მრავალი ტრიგონომეტრიული ფორმულა, რომლებიც არსებითად იგივე იდენტობებია.

მართლაც, ორი წევრის ჯამის კვადრატი უდრის პირველის კვადრატს პლუს ორჯერ ნამრავლი პირველის მეორეზე და პლუს მეორის კვადრატი, ანუ (a+b)^2= (a+ ბ)(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

გაამარტივეთ ორივე

გადაწყვეტის ზოგადი პრინციპები

გაიმეორეთ მათემატიკური ანალიზის ან უმაღლესი მათემატიკის სახელმძღვანელოდან რა არის განსაზღვრული ინტეგრალი. როგორც ცნობილია, განსაზღვრული ინტეგრალის ამონახსნი არის ფუნქცია, რომლის წარმოებული მისცემს ინტეგრანდს. ამ ფუნქციას ანტიდერივატი ეწოდება. ამ პრინციპის საფუძველზე აგებულია ძირითადი ინტეგრალები.
განსაზღვრეთ ინტეგრადის ტიპის მიხედვით, ცხრილის რომელი ინტეგრალია შესაფერისი ამ შემთხვევაში. ამის დაუყოვნებლივ დადგენა ყოველთვის არ არის შესაძლებელი. ხშირად, ტაბულური ფორმა შესამჩნევი ხდება მხოლოდ რამდენიმე გარდაქმნის შემდეგ, ინტეგრადის გასამარტივებლად.

ცვლადის ჩანაცვლების მეთოდი

თუ ინტეგრადი არის ტრიგონომეტრიული ფუნქცია, რომლის არგუმენტი არის პოლინომი, მაშინ სცადეთ გამოიყენოთ ცვლადების შეცვლის მეთოდი. ამისათვის შეცვალეთ პოლინომი ინტეგრადის არგუმენტში ახალი ცვლადით. ახალ და ძველ ცვლადებს შორის ურთიერთობის საფუძველზე განსაზღვრეთ ინტეგრაციის ახალი საზღვრები. ამ გამონათქვამის დიფერენცირებით იპოვეთ ახალი დიფერენციალი . ამრიგად, თქვენ მიიღებთ წინა ინტეგრალის ახალ ფორმას, ახლოს ან თუნდაც რომელიმე ცხრილის შესაბამისს.

მეორე სახის ინტეგრალების ამოხსნა

თუ ინტეგრალი არის მეორე სახის ინტეგრალი, ინტეგრანის ვექტორული ფორმა, მაშინ დაგჭირდებათ ამ ინტეგრალებიდან სკალარზე გადასვლის წესების გამოყენება. ერთ-ერთი ასეთი წესია ოსტროგრადსკი-გაუსის ურთიერთობა. ეს კანონი საშუალებას გვაძლევს გადავიდეთ გარკვეული ვექტორული ფუნქციის როტორული ნაკადიდან სამმაგ ინტეგრალზე მოცემული ვექტორული ველის დივერგენციაზე.

ინტეგრაციის ლიმიტების ჩანაცვლება

ანტიდერივატივის პოვნის შემდეგ აუცილებელია ინტეგრაციის საზღვრების ჩანაცვლება. პირველ რიგში, ჩაანაცვლეთ ზედა ზღვრის მნიშვნელობა ანტიწარმოებულის გამოხატულებაში. რაღაც ნომერს მიიღებ. შემდეგ, მიღებული რიცხვიდან გამოაკლეთ ქვედა ზღვრიდან მიღებული სხვა რიცხვი ანტიწარმოებულში. თუ ინტეგრაციის ერთ-ერთი ლიმიტი არის უსასრულობა, მაშინ მისი ანტიდერივატიულ ფუნქციაში ჩანაცვლებისას აუცილებელია ზღვარზე გადასვლა და იმის პოვნა, რისკენ მიდრეკილია გამოხატულება.
თუ ინტეგრალი არის ორგანზომილებიანი ან სამგანზომილებიანი, მაშინ თქვენ მოგიწევთ გეომეტრიულად წარმოადგინოთ ინტეგრაციის საზღვრები, რათა გაიგოთ, როგორ შეაფასოთ ინტეგრალი. მართლაც, მაგალითად, სამგანზომილებიანი ინტეგრალის შემთხვევაში, ინტეგრაციის საზღვრები შეიძლება იყოს მთლიანი სიბრტყეები, რომლებიც ზღუდავს ინტეგრირებულ მოცულობას.

ლოგარითმის განმარტება

b-ის ლოგარითმი a ფუძემდე არის ის მაჩვენებელი, რომელზეც a უნდა გაიზარდოს b-ის მისაღებად.

ნომერი ემათემატიკაში ჩვეულებრივია აღვნიშნოთ ის ზღვარი, რომლისკენაც მიისწრაფვის გამოხატვა

ნომერი ეარის ირაციონალური რიცხვი- რიცხვი ერთთან შეუდარებელია, ის ზუსტად ვერ გამოისახება როგორც მთელი რიცხვი და არც წილადი რაციონალურინომერი.

წერილი ე- ლათინური სიტყვის პირველი ასო განმხილველი- საჩვენებლად, აქედან მომდინარეობს სახელი მათემატიკაში ექსპონენციალური- ექსპონენციალური ფუნქცია.

ნომერი ეფართოდ გამოიყენება მათემატიკაში და ყველა მეცნიერებაში, რომლებიც ამა თუ იმ გზით იყენებენ მათემატიკურ გამოთვლებს თავიანთი საჭიროებისთვის.

ლოგარითმები. ლოგარითმების თვისებები

განმარტება: b დადებითი რიცხვის ლოგარითმი მის ფუძეზე არის c მაჩვენებელი, რომელზეც უნდა გაიზარდოს რიცხვი a რიცხვის მისაღებად.

ძირითადი ლოგარითმული იდენტურობა:

7) ახალ ბაზაზე გადასვლის ფორმულა:

lna = log e a, e ≈ 2.718…

ამოცანები და ტესტები თემაზე „ლოგარითმები. ლოგარითმების თვისებები"

• ლოგარითმები - მნიშვნელოვანი თემები მათემატიკაში ერთიანი სახელმწიფო გამოცდის განხილვისათვის

ამ თემაზე ამოცანების წარმატებით შესასრულებლად, თქვენ უნდა იცოდეთ ლოგარითმის განმარტება, ლოგარითმის თვისებები, ძირითადი ლოგარითმული იდენტურობა, ათობითი და ბუნებრივი ლოგარითმების განმარტებები. ამ თემაზე ამოცანების ძირითადი ტიპები არის პრობლემები, რომლებიც დაკავშირებულია ლოგარითმული გამონათქვამების გამოთვლასა და ტრანსფორმაციასთან. განვიხილოთ მათი გადაწყვეტა შემდეგი მაგალითების გამოყენებით.

გამოსავალი:ლოგარითმების თვისებების გამოყენებით ვიღებთ

გამოსავალი:გრადუსების თვისებების გამოყენებით ვიღებთ

1) (2 2) ჟურნალი 2 5 =(2 ჟურნალი 2 5) 2 =5 2 =25

ლოგარითმების თვისებები, ფორმულირებები და მტკიცებულებები.

ლოგარითმს აქვს მრავალი დამახასიათებელი თვისება. ამ სტატიაში განვიხილავთ მთავარს ლოგარითმების თვისებები. აქ ჩვენ მივცემთ მათ ფორმულირებებს, ჩამოვწერთ ლოგარითმების თვისებებს ფორმულების სახით, ვაჩვენებთ მათი გამოყენების მაგალითებს და ასევე დავადასტურებთ ლოგარითმების თვისებებს.

გვერდის ნავიგაცია.

ლოგარითმების ძირითადი თვისებები, ფორმულები

დამახსოვრებისა და გამოყენების სიმარტივისთვის, წარმოვიდგინოთ ლოგარითმის ძირითადი თვისებებიფორმულების სიის სახით. მომდევნო აბზაცში მივცემთ მათ ფორმულირებებს, მტკიცებულებებს, გამოყენების მაგალითებს და აუცილებელ განმარტებებს.

ერთიანობის ლოგარითმის თვისება: log a 1=0 ნებისმიერი a>0, a≠1.

ფუძის ტოლი რიცხვის ლოგარითმი: log a a=1 a>0, a≠1-ისთვის.

ფუძის სიმძლავრის ლოგარითმის თვისება: log a a p =p, სადაც a>0, a≠1 და p არის ნებისმიერი რეალური რიცხვი.

ორი დადებითი რიცხვის ნამრავლის ლოგარითმი: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
და n დადებითი რიცხვის ნამრავლის ლოგარითმის თვისება: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0.

კოეფიციენტის ლოგარითმის თვისება: , სადაც a>0, a≠1, x>0, y>0.

რიცხვის სიმძლავრის ლოგარითმი: log a b p =p·log a |b| , სადაც a>0, a≠1, b და p ისეთი რიცხვებია, რომ b p ხარისხი აქვს აზრი და b p >0.

შედეგი: , სადაც a>0, a≠1, n არის ერთზე მეტი ნატურალური რიცხვი, b>0.

დასკვნა 1: , a>0 , a≠1 , b>0 , b≠1 .

დასკვნა 2: , a>0 , a≠1 , b>0 , p და q ნამდვილი რიცხვებია, q≠0 , კერძოდ b=a-სთვის გვაქვს .

ფორმულირებები და თვისებების დადასტურება

ჩვენ ვაგრძელებთ ლოგარითმების წერილობითი თვისებების ფორმულირებას და მტკიცებას. ლოგარითმის ყველა თვისება დადასტურებულია ლოგარითმის განმარტებისა და მისგან გამომდინარე ძირითადი ლოგარითმული იდენტობის, აგრეთვე ხარისხის თვისებების საფუძველზე.

დავიწყოთ იმით ერთის ლოგარითმის თვისებები. მისი ფორმულირება ასეთია: ერთიანობის ლოგარითმი ნულის ტოლია, ანუ შესვლა a 1=0ნებისმიერი a>0, a≠1. მტკიცებულება არ არის რთული: ვინაიდან 0 =1 ნებისმიერი a-სთვის, რომელიც აკმაყოფილებს ზემოთ მოცემულ პირობებს a>0 და a≠1, მაშინ დასამტკიცებელი ტოლობის ჟურნალი a 1=0 დაუყოვნებლივ გამომდინარეობს ლოგარითმის განმარტებიდან.

მოვიყვანოთ განხილული თვისების გამოყენების მაგალითები: log 3 1=0, log1=0 და .

გადავიდეთ შემდეგ ქონებაზე: ფუძის ტოლი რიცხვის ლოგარითმი ერთის ტოლია, ანუ შესვლა a=1 a>0, a≠1. მართლაც, ვინაიდან a 1 =a ნებისმიერი a-სთვის, მაშინ ლოგარითმის განმარტებით log a=1.

ლოგარითმების ამ თვისების გამოყენების მაგალითებია ტოლობები log 5 5=1, log 5.6 5.6 და lne=1.

რიცხვის სიმძლავრის ლოგარითმი, რომელიც ტოლია ლოგარითმის ფუძის ტოლია, მაჩვენებლის ტოლია. ლოგარითმის ეს თვისება შეესაბამება ფორმის ფორმულას შესვლა a p =p, სადაც a>0, a≠1 და p – ნებისმიერი რეალური რიცხვი. ეს თვისება პირდაპირ გამომდინარეობს ლოგარითმის განმარტებიდან. გაითვალისწინეთ, რომ ის საშუალებას გაძლევთ დაუყოვნებლივ მიუთითოთ ლოგარითმის მნიშვნელობა, თუ შესაძლებელია ლოგარითმის ნიშნის ქვეშ მყოფი რიცხვის წარმოდგენა, როგორც ფუძის სიმძლავრე; ამაზე მეტს ვისაუბრებთ ლოგარითმის გამოთვლის სტატიაში.

მაგალითად, log 2 2 7 =7, log10 -4 =-4 და .

ორი დადებითი რიცხვის ნამრავლის ლოგარითმი x და y ტოლია ამ რიცხვების ლოგარითმების ნამრავლის: log a (x y)=log a x+log a y, a>0 , a≠1 . მოდით დავამტკიცოთ პროდუქტის ლოგარითმის თვისება. a log a x+log a y =a log a x ·a log a y, და რადგან მთავარი ლოგარითმული იდენტობის მიხედვით a log a x =x და log a y =y, მაშინ log a x ·a log a y =x· y. ამრიგად, log a x+log a y =x·y, საიდანაც, ლოგარითმის განმარტებით, დადასტურებული ტოლობა გამომდინარეობს.

ვაჩვენოთ ნამრავლის ლოგარითმის თვისების გამოყენების მაგალითები: log 5 (2 3)=log 5 2+log 5 3 და .

ნამრავლის ლოგარითმის თვისება შეიძლება განზოგადდეს დადებითი რიცხვების n სასრული რიცხვის ნამრავლზე x 1 , x 2 , …, x n როგორც log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. ეს თანასწორობა შეიძლება დადასტურდეს უპრობლემოდ მათემატიკური ინდუქციის მეთოდის გამოყენებით.

მაგალითად, პროდუქტის ბუნებრივი ლოგარითმი შეიძლება შეიცვალოს 4, e და რიცხვების სამი ბუნებრივი ლოგარითმის ჯამით.

ორი დადებითი რიცხვის კოეფიციენტის ლოგარითმი x და y უდრის სხვაობას ამ რიცხვების ლოგარითმებს შორის. კოეფიციენტის ლოგარითმის თვისება შეესაბამება ფორმის ფორმულას , სადაც a>0, a≠1, x და y არის რამდენიმე დადებითი რიცხვი. დადასტურებულია ამ ფორმულის მართებულობა, ისევე როგორც პროდუქტის ლოგარითმის ფორმულა: ვინაიდან , შემდეგ ლოგარითმის განმარტებით .

აქ მოცემულია ლოგარითმის ამ თვისების გამოყენების მაგალითი: .

მოდით გადავიდეთ სიმძლავრის ლოგარითმის თვისება. ხარისხის ლოგარითმი ტოლია ამ ხარისხის მაჩვენებლის და ამ ხარისხის ფუძის მოდულის ლოგარითმის ნამრავლის. მოდით დავწეროთ სიმძლავრის ლოგარითმის ეს თვისება ფორმულის სახით: log a b p =p·log a |b|, სადაც a>0, a≠1, b და p ისეთი რიცხვებია, რომ b p ხარისხი აქვს აზრი და b p >0.

ჯერ ვამტკიცებთ ამ თვისებას დადებითად b. ძირითადი ლოგარითმული იდენტურობა გვაძლევს საშუალებას გამოვსახოთ რიცხვი b, როგორც log a b , შემდეგ b p =(a log a b) p , და მიღებული გამოხატულება, ძალაუფლების თვისების გამო, უდრის p·log a b. ასე რომ, მივდივართ ტოლობამდე b p =a p·log a b, საიდანაც, ლოგარითმის განმარტებით, ვასკვნით, რომ log a b p =p·log a b.

რჩება ამ თვისების დამტკიცება უარყოფითი ბ. აქვე აღვნიშნავთ, რომ გამოთქმა log a b p უარყოფითი b-ისთვის აზრი აქვს მხოლოდ ლუწი მაჩვენებლებს p (რადგან b ხარისხის b p მნიშვნელობა უნდა იყოს ნულზე მეტი, წინააღმდეგ შემთხვევაში ლოგარითმი აზრი არ ექნება) და ამ შემთხვევაში b p =|b| გვ. შემდეგ b p =|b| p =(a log a |b|) p =a p·log a |b| , საიდანაც log a b p =p·log a |b| .

Მაგალითად, და ln(-3) 4 =4·ln|-3|=4·ln3.

ეს გამომდინარეობს წინა საკუთრებიდან ლოგარითმის თვისება ფესვიდან: n-ე ფესვის ლოგარითმი უდრის 1/n წილადის ნამრავლს რადიკალური გამოხატვის ლოგარითმით, ანუ სადაც a>0, a≠1, n არის ერთზე მეტი ნატურალური რიცხვი, b>0. .

მტკიცებულება ეფუძნება ტოლობას (იხ. მაჩვენებლის განმარტება წილადის მაჩვენებლით), რომელიც მოქმედებს ნებისმიერი დადებითი b-ისთვის და მაჩვენებლის ლოგარითმის თვისებაზე: .

აქ მოცემულია ამ ქონების გამოყენების მაგალითი: .

ახლა დავამტკიცოთ ახალ ლოგარითმის ბაზაზე გადასვლის ფორმულაკეთილი . ამისათვის საკმარისია დავამტკიცოთ ტოლობის log c b=log a b·log c a. ძირითადი ლოგარითმული იდენტობა საშუალებას გვაძლევს გამოვიტანოთ რიცხვი b როგორც log a b , შემდეგ log c b=log c a log a b . რჩება ხარისხის ლოგარითმის თვისების გამოყენება: log c a log a b =log a b·log c a . ეს ადასტურებს ტოლობის log c b=log a b·log c a, რაც ნიშნავს, რომ ასევე დადასტურებულია ლოგარითმის ახალ ბაზაზე გადასვლის ფორმულა. .

მოდით ვნახოთ ლოგარითმების ამ თვისების გამოყენების რამდენიმე მაგალითი: და .

ახალ ბაზაზე გადასვლის ფორმულა საშუალებას გაძლევთ გადახვიდეთ ლოგარითმებთან მუშაობაზე, რომლებსაც აქვთ "მოხერხებული" ბაზა. მაგალითად, ის შეიძლება გამოყენებულ იქნას ბუნებრივ ან ათობითი ლოგარითმებზე გადასასვლელად, რათა გამოთვალოთ ლოგარითმის მნიშვნელობა ლოგარითმების ცხრილიდან. ახალ ლოგარითმის ბაზაზე გადასვლის ფორმულა ასევე საშუალებას იძლევა, ზოგიერთ შემთხვევაში, იპოვოთ მოცემული ლოგარითმის მნიშვნელობა, როდესაც ცნობილია ზოგიერთი ლოგარითმის მნიშვნელობები სხვა ბაზებთან.

ხშირად გამოიყენება ფორმის c=b-სთვის ახალ ლოგარითმის ბაზაზე გადასვლის ფორმულის სპეციალური შემთხვევა. ეს აჩვენებს, რომ log a b და log b a ურთიერთშებრუნებული რიცხვებია. Მაგალითად, .

ასევე ხშირად გამოიყენება ფორმულა, რომელიც მოსახერხებელია ლოგარითმების მნიშვნელობების მოსაძებნად. ჩვენი სიტყვების დასადასტურებლად, ჩვენ ვაჩვენებთ, თუ როგორ შეიძლება მისი გამოყენება ფორმის ლოგარითმის მნიშვნელობის გამოსათვლელად. Ჩვენ გვაქვს . ფორმულის დასამტკიცებლად საკმარისია გამოვიყენოთ ფორმულა ლოგარითმის ახალ ბაზაზე გადასასვლელად a: .

რჩება ლოგარითმების შედარების თვისებების დამტკიცება.

გამოვიყენოთ საპირისპირო მეთოდი. დავუშვათ, რომ 1 >1, 2 >1 და 1 2 და 0 1-ისთვის, log a 1 b≤log a 2 b მართალია. ლოგარითმების თვისებებზე დაყრდნობით, ეს უტოლობები შეიძლება გადაიწეროს როგორც და შესაბამისად, და მათგან გამომდინარეობს, რომ log b a 1 ≤log b a 2 და log b a 1 ≥log b a 2, შესაბამისად. შემდეგ, იგივე საფუძვლების მქონე ხარისხების თვისებების მიხედვით, უნდა იყოს ტოლობები b log b a 1 ≥b log b a 2 და b log b a 1 ≥b log b a 2, ანუ a 1 ≥a 2 . ასე რომ, ჩვენ მივედით წინააღმდეგობაში პირობასთან a 1 2. ეს ასრულებს მტკიცებულებას.

ლოგარითმების ძირითადი თვისებები

• მასალა გაკვეთილისთვის
• ჩამოტვირთეთ ყველა ფორმულა

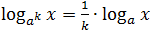
ლოგარითმები, ისევე როგორც ნებისმიერი რიცხვი, შეიძლება ყველანაირად დაემატოს, გამოკლდეს და გარდაიქმნას. მაგრამ რადგან ლოგარითმები არ არის ზუსტად ჩვეულებრივი რიცხვები, აქ არის წესები, რომლებსაც უწოდებენ ძირითადი თვისებები.

თქვენ აუცილებლად უნდა იცოდეთ ეს წესები - მათ გარეშე არც ერთი სერიოზული ლოგარითმული პრობლემის გადაჭრა შეუძლებელია. გარდა ამისა, ისინი ძალიან ცოტაა - ყველაფრის სწავლა ერთ დღეში შეგიძლიათ. ასე რომ, დავიწყოთ.

ლოგარითმების შეკრება და გამოკლება

განვიხილოთ ორი ლოგარითმი ერთნაირი ფუძეებით: log a x და log a y. შემდეგ მათი დამატება და გამოკლება შესაძლებელია და:

მაშასადამე, ლოგარითმების ჯამი ტოლია ნამრავლის ლოგარითმისა, ხოლო სხვაობა უდრის კოეფიციენტის ლოგარითმს. გთხოვთ გაითვალისწინოთ: მთავარი აქ არის იდენტური საფუძველი. თუ მიზეზები განსხვავებულია, ეს წესები არ მუშაობს!

ეს ფორმულები დაგეხმარებათ გამოთვალოთ ლოგარითმული გამოხატულება მაშინაც კი, როცა მისი ცალკეული ნაწილები არ არის გათვალისწინებული (იხილეთ გაკვეთილი „რა არის ლოგარითმი“). გადახედეთ მაგალითებს და ნახეთ:

დავალება. იპოვეთ გამოთქმის მნიშვნელობა: log 6 4 + log 6 9.

ვინაიდან ლოგარითმებს აქვთ იგივე ფუძეები, ვიყენებთ ჯამის ფორმულას:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

დავალება. იპოვეთ გამოთქმის მნიშვნელობა: log 2 48 − log 2 3.

საფუძვლები იგივეა, ჩვენ ვიყენებთ განსხვავების ფორმულას:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

დავალება. იპოვეთ გამოთქმის მნიშვნელობა: log 3 135 − log 3 5.

ისევ ბაზები იგივეა, ამიტომ გვაქვს:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

როგორც ხედავთ, ორიგინალური გამონათქვამები შედგება "ცუდი" ლოგარითმებისგან, რომლებიც ცალკე არ არის გამოთვლილი. მაგრამ გარდაქმნების შემდეგ მიიღება სრულიად ნორმალური რიცხვები. ბევრი ტესტი ეფუძნება ამ ფაქტს. დიახ, ტესტის მსგავსი გამონათქვამები წარმოდგენილია მთელი სერიოზულობით (ზოგჯერ პრაქტიკულად ცვლილებების გარეშე) ერთიან სახელმწიფო გამოცდაზე.

მაჩვენებლის ამოღება ლოგარითმიდან

ახლა ცოტა გავართულოთ დავალება. რა მოხდება, თუ ლოგარითმის საფუძველი ან არგუმენტი არის ძალა? მაშინ ამ ხარისხის მაჩვენებლის ამოღება შესაძლებელია ლოგარითმის ნიშნიდან შემდეგი წესების მიხედვით:

• log a x n = n · log a x ;
• 
• 

ადვილი მისახვედრია, რომ ბოლო წესი პირველ ორს მიჰყვება. მაგრამ უმჯობესია დაიმახსოვროთ ის მაინც - ზოგიერთ შემთხვევაში ეს მნიშვნელოვნად შეამცირებს გამოთვლების რაოდენობას.

რა თქმა უნდა, ყველა ამ წესს აქვს აზრი, თუ ლოგარითმის ODZ დაფიქსირდა: a > 0, a ≠ 1, x > 0. და კიდევ ერთი რამ: ისწავლეთ ყველა ფორმულის გამოყენება არა მხოლოდ მარცხნიდან მარჯვნივ, არამედ პირიქით. , ე.ი. თქვენ შეგიძლიათ შეიყვანოთ რიცხვები ლოგარითმის ნიშანიმდე ლოგარითმში. ეს არის ის, რაც ყველაზე ხშირად საჭიროა.

დავალება. იპოვეთ გამოთქმის მნიშვნელობა: log 7 49 6 .

მოდით, თავი დავაღწიოთ არგუმენტის ხარისხს პირველი ფორმულის გამოყენებით:
ჟურნალი 7 49 6 = 6 ჟურნალი 7 49 = 6 2 = 12

დავალება. იპოვნეთ გამოთქმის მნიშვნელობა:

[წარწერა სურათზე]

გაითვალისწინეთ, რომ მნიშვნელი შეიცავს ლოგარითმს, რომლის საფუძველი და არგუმენტი ზუსტი ხარისხებია: 16 = 2 4; 49 = 7 2. Ჩვენ გვაქვს:

[წარწერა სურათზე]

ვფიქრობ, ბოლო მაგალითი მოითხოვს გარკვეულ განმარტებას. სად წავიდა ლოგარითმები? ბოლო მომენტამდე ჩვენ ვმუშაობთ მხოლოდ მნიშვნელით. იქ მდგომი ლოგარითმის საფუძველი და არგუმენტი წარვადგინეთ სიმძლავრეების სახით და ამოვიღეთ მაჩვენებლები - მივიღეთ „სამსართულიანი“ წილადი.

ახლა გადავხედოთ ძირითად წილადს. მრიცხველი და მნიშვნელი შეიცავს ერთსა და იმავე რიცხვს: log 2 7. ვინაიდან log 2 7 ≠ 0, შეგვიძლია შევამციროთ წილადი - 2/4 დარჩება მნიშვნელში. არითმეტიკის წესების მიხედვით, ოთხი შეიძლება გადავიდეს მრიცხველზე, რაც გაკეთდა. შედეგი იყო პასუხი: 2.

ახალ საძირკველზე გადასვლა

ლოგარითმების შეკრების და გამოკლების წესებზე საუბრისას, მე კონკრეტულად ხაზგასმით აღვნიშნე, რომ ისინი მუშაობენ მხოლოდ ერთი და იგივე ფუძეებით. რა მოხდება, თუ მიზეზები განსხვავებულია? რა მოხდება, თუ ისინი არ არიან იგივე რიცხვის ზუსტი სიმძლავრეები?

ახალ საძირკველზე გადასვლის ფორმულები სამაშველოში მოდის. მოდით ჩამოვაყალიბოთ ისინი თეორემის სახით:

დაე, ლოგარითმი log a x იყოს მოცემული. მაშინ ნებისმიერი c რიცხვისთვის ისეთი, რომ c > 0 და c ≠ 1, ტოლობა მართალია:

[წარწერა სურათზე]

კერძოდ, თუ დავაყენებთ c = x, მივიღებთ:

[წარწერა სურათზე]

მეორე ფორმულიდან გამომდინარეობს, რომ ლოგარითმის საფუძველი და არგუმენტი შეიძლება შეიცვალოს, მაგრამ ამ შემთხვევაში მთელი გამოთქმა „გადატრიალებულია“, ე.ი. ლოგარითმი გამოჩნდება მნიშვნელში.

ეს ფორმულები იშვიათად გვხვდება ჩვეულებრივ ციფრულ გამონათქვამებში. მათი მოხერხებულობის შეფასება შესაძლებელია მხოლოდ ლოგარითმული განტოლებებისა და უტოლობების ამოხსნისას.

თუმცა არის პრობლემები, რომელთა მოგვარებაც საერთოდ შეუძლებელია, გარდა ახალ ფონდში გადასვლისა. მოდით შევხედოთ რამდენიმე მათგანს:

დავალება. იპოვეთ გამოთქმის მნიშვნელობა: log 5 16 log 2 25.

გაითვალისწინეთ, რომ ორივე ლოგარითმის არგუმენტები შეიცავს ზუსტ ძალას. ამოვიღოთ ინდიკატორები: log 5 16 = log 5 2 4 = 4log 5 2; ჟურნალი 2 25 = ჟურნალი 2 5 2 = 2ლოგი 2 5;

ახლა მოდით "შევუბრუნდეთ" მეორე ლოგარითმს:

[წარწერა სურათზე]

ვინაიდან პროდუქტი არ იცვლება ფაქტორების გადაწყობისას, ჩვენ მშვიდად გავამრავლეთ ოთხი და ორი, შემდეგ კი ლოგარითმებს მივმართეთ.

დავალება. იპოვეთ გამოთქმის მნიშვნელობა: log 9 100 lg 3.

პირველი ლოგარითმის საფუძველი და არგუმენტი ზუსტი სიმძლავრეებია. მოდით დავწეროთ ეს და მოვიშოროთ ინდიკატორები:

[წარწერა სურათზე]

ახლა მოდით დავაღწიოთ ათობითი ლოგარითმი ახალ ბაზაზე გადასვლით:

[წარწერა სურათზე]

ძირითადი ლოგარითმული იდენტურობა

ხშირად ამოხსნის პროცესში აუცილებელია რიცხვის ლოგარითმის სახით წარმოდგენა მოცემულ ბაზაზე. ამ შემთხვევაში შემდეგი ფორმულები დაგვეხმარება:

1. n = log a a n

2. პირველ შემთხვევაში, რიცხვი n ხდება არგუმენტის მაჩვენებელი. რიცხვი n შეიძლება იყოს აბსოლუტურად ნებისმიერი, რადგან ის მხოლოდ ლოგარითმის მნიშვნელობაა.

   მეორე ფორმულა რეალურად არის პერიფრაზირებული განმარტება. სწორედ ამას ჰქვია: ძირითადი ლოგარითმული იდენტობა.

   ფაქტობრივად, რა მოხდება, თუ რიცხვი b გაიზარდა ისეთ ხარისხამდე, რომ რიცხვი b ამ ხარისხში იძლევა რიცხვს a? მართალია: შედეგი არის იგივე რიცხვი a. კიდევ ერთხელ ყურადღებით წაიკითხეთ ეს აბზაცი - ბევრი ადამიანი ჩერდება მასზე.

   ახალ ბაზაზე გადასვლის ფორმულების მსგავსად, ძირითადი ლოგარითმული იდენტურობა ზოგჯერ ერთადერთი შესაძლო გამოსავალია.

   [წარწერა სურათზე]

   გაითვალისწინეთ, რომ log 25 64 = log 5 8 - ჩვენ უბრალოდ ავიღეთ კვადრატი ლოგარითმის ფუძიდან და არგუმენტიდან. იმავე ფუძით ძალაუფლების გამრავლების წესების გათვალისწინებით, მივიღებთ:

   [წარწერა სურათზე]

   თუ ვინმემ არ იცის, ეს იყო რეალური დავალება ერთიანი სახელმწიფო გამოცდიდან :)

   ლოგარითმული ერთეული და ლოგარითმული ნული

   დასასრულს, მე მივცემ ორ იდენტობას, რომლებსაც ძნელად შეიძლება ვუწოდოთ თვისებები - უფრო მეტიც, ისინი ლოგარითმის განსაზღვრის შედეგებია. ისინი გამუდმებით ჩნდებიან პრობლემებში და, რა გასაკვირია, პრობლემებს უქმნიან თუნდაც „მოწინავე“ მოსწავლეებს.

   1. log a a = 1 არის ლოგარითმული ერთეული. ერთხელ და სამუდამოდ დაიმახსოვრეთ: ლოგარითმი ამ ფუძის ნებისმიერი a ფუძის ტოლია ერთის.
   2. log a 1 = 0 არის ლოგარითმული ნული. ფუძე a შეიძლება იყოს ნებისმიერი, მაგრამ თუ არგუმენტი შეიცავს ერთს, ლოგარითმი ნულის ტოლია! რადგან 0 = 1 არის განმარტების პირდაპირი შედეგი.

   ეს არის ყველა თვისება. დარწმუნდით, რომ ივარჯიშეთ მათ პრაქტიკაში! ჩამოტვირთეთ მოტყუების ფურცელი გაკვეთილის დასაწყისში, ამობეჭდეთ და მოაგვარეთ პრობლემები.

   ლოგარითმი. ლოგარითმის თვისებები (შეკრება და გამოკლება).

   ლოგარითმის თვისებებიდაიცავით მისი განმარტება. ასე რომ, რიცხვის ლოგარითმი ბდაფუძნებული აგანისაზღვრება, როგორც მაჩვენებელი, რომელზეც რიცხვი უნდა გაიზარდოს ანომრის მისაღებად ბ(ლოგარითმი არსებობს მხოლოდ დადებითი რიცხვებისთვის).

   ამ ფორმულირებიდან გამომდინარეობს, რომ გაანგარიშება x=log a b, უდრის განტოლების ამოხსნას a x =b.Მაგალითად, ჟურნალი 2 8 = 3რადგან 8 = 2 3 . ლოგარითმის ფორმულირება იძლევა იმის დასაბუთებას, რომ თუ b=a გ, შემდეგ რიცხვის ლოგარითმი ბდაფუძნებული აუდრის თან. ასევე ნათელია, რომ ლოგარითმების თემა მჭიდრო კავშირშია ძალაუფლების თემასთან.

   ლოგარითმებით, როგორც ნებისმიერი რიცხვით, შეგიძლიათ ამის გაკეთება შეკრების, გამოკლების ოპერაციებიდა გარდაიქმნება ყველა შესაძლო გზით. მაგრამ იმის გამო, რომ ლოგარითმები არ არის სრულიად ჩვეულებრივი რიცხვები, აქ მოქმედებს მათი სპეციალური წესები, რომლებიც ე.წ. ძირითადი თვისებები.

   ლოგარითმების შეკრება და გამოკლება.

   ავიღოთ ორი ლოგარითმი ერთი და იგივე ფუძეებით: შესვლა xდა შესვლა y. შემდეგ შესაძლებელია შეკრებისა და გამოკლების ოპერაციების შესრულება:

   როგორც ვხედავთ, ლოგარითმების ჯამიუდრის პროდუქტის ლოგარითმს და განსხვავება ლოგარითმები- კოეფიციენტის ლოგარითმი. უფრო მეტიც, ეს მართალია, თუ რიცხვები ა, Xდა ზედადებითი და a ≠ 1.

   მნიშვნელოვანია აღინიშნოს, რომ ამ ფორმულების მთავარი ასპექტი არის იგივე საფუძვლები. თუ საფუძვლები განსხვავებულია, ეს წესები არ მოქმედებს!

   ერთი და იგივე ფუძით ლოგარითმების შეკრებისა და გამოკლების წესები იკითხება არა მხოლოდ მარცხნიდან მარჯვნივ, არამედ პირიქით. შედეგად, ჩვენ გვაქვს ნამრავლის ლოგარითმის თეორემები და კოეფიციენტის ლოგარითმი.

   პროდუქტის ლოგარითმიორი დადებითი რიცხვი უდრის მათი ლოგარითმების ჯამს ; ამ თეორემის ხელახლა ჩამოყალიბებით მივიღებთ შემდეგს, თუ რიცხვები ა, xდა ზედადებითი და a ≠ 1, ეს:

   კოეფიციენტის ლოგარითმიორი დადებითი რიცხვი უდრის დივიდენდისა და გამყოფის ლოგარითმებს შორის სხვაობას. სხვანაირად რომ ვთქვათ, თუ რიცხვები ა, Xდა ზედადებითი და a ≠ 1, ეს:

   გამოვიყენოთ ზემოაღნიშნული თეორემები ამოსახსნელად მაგალითები:

   თუ ნომრები xდა ზეუარყოფითია, მაშინ პროდუქტის ლოგარითმის ფორმულაუაზრო ხდება. ამრიგად, აკრძალულია დაწერა:

   ვინაიდან გამონათქვამები log 2 (-8) და log 2 (-4) საერთოდ არ არის განსაზღვრული (ლოგარითმული ფუნქცია ზე= ჟურნალი 2 Xგანისაზღვრება მხოლოდ დადებითი არგუმენტების მნიშვნელობებისთვის X).

   პროდუქტის თეორემაგამოიყენება არა მხოლოდ ორი, არამედ შეუზღუდავი რაოდენობის ფაქტორებისთვის. ეს ნიშნავს, რომ ყოველი ბუნებრივი კდა ნებისმიერი დადებითი რიცხვი x 1 , x 2 , . . . ,x nარსებობს პირადობა:

   დან ლოგარითმის კოეფიციენტის თეორემაშეიძლება მივიღოთ ლოგარითმის კიდევ ერთი თვისება. საყოველთაოდ ცნობილია, რომ ჟურნალი ა 1 = 0, შესაბამისად

   ეს ნიშნავს, რომ არსებობს თანასწორობა:

   ორი საპასუხო რიცხვის ლოგარითმებიამავე მიზეზით განსხვავდებიან ერთმანეთისაგან მხოლოდ ნიშნით. Ისე:

   ლოგარითმი. ლოგარითმების თვისებები

   ლოგარითმი. ლოგარითმების თვისებები

   განვიხილოთ თანასწორობა. შეგვატყობინეთ და და ჩვენ გვინდა ვიპოვოთ ღირებულებები.

   ანუ, ჩვენ ვეძებთ იმ მაჩვენებელს, რომლითაც ჩვენ უნდა დავამტკიცოთ ის, რომ მივიღოთ.

   დაე ცვლადს შეუძლია მიიღოს ნებისმიერი რეალური მნიშვნელობა, შემდეგ ცვლადებზე დაწესებულია შემდეგი შეზღუდვები: o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″ />

   თუ ჩვენ ვიცით და-ს მნიშვნელობები და გვაქვს ამოცანის პოვნა უცნობი, მაშინ ამ მიზნით შემოდის მათემატიკური ოპერაცია, რომელიც ე.წ. ლოგარითმი.

   ვიპოვოთ ღირებულება, რომელსაც ვიღებთ რიცხვის ლოგარითმიავტორი საფუძველი :

   რიცხვის ლოგარითმი მის ფუძემდე არის ის მაჩვენებელი, რომელზეც ის უნდა გაიზარდოს, რომ მიიღოთ .

   ანუ ძირითადი ლოგარითმული იდენტურობა:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   არსებითად მათემატიკური აღნიშვნაა ლოგარითმის განმარტებები.

   ლოგარითმის მათემატიკური მოქმედება არის ინვერსიული მოქმედების სიძლიერე, ასე ლოგარითმების თვისებებიმჭიდროდ არის დაკავშირებული ხარისხის თვისებებთან.

   ჩამოვთვალოთ მთავარი ლოგარითმების თვისებები:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ სათაური=”d1″/>

   4.

   5.

   თვისებების შემდეგი ჯგუფი საშუალებას გაძლევთ წარმოადგინოთ გამოხატვის გამოხატულება ლოგარითმის ნიშნის ქვეშ, ან ლოგარითმის ფუძეზე დგომა კოეფიციენტის სახით ლოგარითმის ნიშნის წინ:

   6.

   7.

   8.

   9.

   ფორმულების შემდეგი ჯგუფი საშუალებას გაძლევთ გადახვიდეთ ლოგარითმიდან მოცემული ფუძით ლოგარითმზე თვითნებური ფუძის მქონე ლოგარითმზე და ე.წ. ახალ ბაზაზე გადასვლის ფორმულები:

   10.

   12. (დასკვნა ქონების 11-დან)

   

   შემდეგი სამი თვისება კარგად არ არის ცნობილი, მაგრამ ისინი ხშირად გამოიყენება ლოგარითმული განტოლებების ამოხსნისას ან ლოგარითმების შემცველი გამონათქვამების გამარტივებისას:

   13.

   14.

   15.

   განსაკუთრებული შემთხვევები:

   — ათობითი ლოგარითმი

   — ბუნებრივი ლოგარითმი

   ლოგარითმების შემცველი გამონათქვამების გამარტივებისას გამოიყენება ზოგადი მიდგომა:

   1. ათობითი წილადებს წარმოვადგენთ ჩვეულებრივ წილადებად.

   2. შერეულ რიცხვებს წარმოვადგენთ არასწორ წილადებად.

   3. ლოგარითმის ფუძეზე და ლოგარითმის ნიშნის ქვეშ არსებულ რიცხვებს ვშლით მარტივ ფაქტორებად.

   4. ჩვენ ვცდილობთ შევამციროთ ყველა ლოგარითმი ერთსა და იმავე ფუძემდე.

   5. გამოიყენეთ ლოგარითმების თვისებები.

   მოდით შევხედოთ ლოგარითმების შემცველი გამონათქვამების გამარტივების მაგალითებს.

   მაგალითი 1.

   გამოთვალეთ:

   მოდით გავამარტივოთ ყველა მაჩვენებლები: ჩვენი ამოცანაა დავიყვანოთ ისინი ლოგარითმებამდე, რომელთა ფუძე იგივე რიცხვია, რაც მაჩვენებლის ფუძეს.

   ==(საკუთრებით 7)=(საკუთრებით 6) =

   მოდით ჩავანაცვლოთ ის ინდიკატორები, რომლებიც მივიღეთ თავდაპირველ გამოხატულებაში. ჩვენ ვიღებთ:

   პასუხი: 5.25

   მაგალითი 2. გამოთვალეთ:

   

   მოდით შევამციროთ ყველა ლოგარითმი 6-მდე (ამ შემთხვევაში, წილადის მნიშვნელის ლოგარითმები "მიგრირდებიან" მრიცხველზე):

   მოდით დავშალოთ რიცხვები ლოგარითმის ნიშნის ქვეშ მარტივ ფაქტორებად:

   მოდით გამოვიყენოთ თვისებები 4 და 6:

   წარმოგიდგენთ ჩანაცვლებას

   ჩვენ ვიღებთ:

   პასუხი: 1

   ლოგარითმი . ძირითადი ლოგარითმული იდენტურობა.

   ლოგარითმების თვისებები. ათწილადი ლოგარითმი. ბუნებრივი ლოგარითმი.

   ლოგარითმი დადებითი რიცხვი N ფუძისთვის (ბ > 0, ბ 1) არის x მაჩვენებელი, რომელზეც b უნდა გაიზარდოს N-ის მისაღებად .

   ეს ჩანაწერი უდრის შემდეგს: b x = N .

   მაგალითები: ჟურნალი 3 81 = 4, ვინაიდან 3 4 = 81;

   ჟურნალი 1/3 27 = – 3, ვინაიდან (1/3) - 3 = 3 3 = 27.

   ლოგარითმის ზემოაღნიშნული განმარტება შეიძლება დაიწეროს როგორც იდენტურობა:

   

   ლოგარითმების ძირითადი თვისებები.

   2) ჟურნალი 1 = 0, ვინაიდან ბ 0 = 1 .

   3) პროდუქტის ლოგარითმი უდრის ფაქტორების ლოგარითმების ჯამს:

   4) კოეფიციენტის ლოგარითმი უდრის დივიდენდისა და გამყოფის ლოგარითმებს შორის სხვაობას:

   5) სიმძლავრის ლოგარითმი ტოლია მაჩვენებლისა და მისი ფუძის ლოგარითმის ნამრავლის:

   ამ ქონების შედეგი შემდეგია: ფესვის ლოგარითმი უდრის რადიკალური რიცხვის ლოგარითმს გაყოფილი ფესვის ძალაზე:

   

   6) თუ ლოგარითმის საფუძველი არის ხარისხი, მაშინ მნიშვნელობა მაჩვენებლის ინვერსია შეიძლება ამოღებულ იქნას ლოგის რითმის სახით:

   

   ბოლო ორი თვისება შეიძლება გაერთიანდეს ერთში:

   

   7) გარდამავალი მოდულის ფორმულა (ანუ ერთი ლოგარითმის ბაზიდან მეორე ბაზაზე გადასვლა):

   

   განსაკუთრებულ შემთხვევაში, როცა N=aჩვენ გვაქვს:

   

   ათწილადი ლოგარითმი დაურეკა ბაზის ლოგარითმი 10. აღინიშნება ლგ, ე.ი. ჟურნალი 10 ნ= ჟურნალი ნ. რიცხვების ლოგარითმები 10, 100, 1000, . p არის 1, 2, 3, ..., შესაბამისად, ე.ი. ბევრი დადებითი აქვს

   ერთეული, რამდენი ნული არის ლოგარითმულ რიცხვში ერთის შემდეგ. რიცხვების ლოგარითმები 0.1, 0.01, 0.001, . p არის შესაბამისად –1, –2, –3, …, ე.ი. აქვს იმდენი უარყოფითი, რამდენიც არის ნულები ლოგარითმულ რიცხვში ერთის წინ (მათ შორის ნულოვანი მთელი რიცხვები). სხვა რიცხვების ლოგარითმებს აქვთ წილადი ნაწილი ე.წ მანტისა. ლოგარითმის მთელი რიცხვი ეწოდება დამახასიათებელი. პრაქტიკული გამოყენებისთვის, ათობითი ლოგარითმები ყველაზე მოსახერხებელია.

   ბუნებრივი ლოგარითმი დაურეკა ბაზის ლოგარითმი ე. იგი აღინიშნება ln-ით, ე.ი. ჟურნალი ე ნ= ჟურნალი ნ. ნომერი ეარის ირაციონალური, მისი სავარაუდო მნიშვნელობა არის 2.718281828. ეს არის ზღვარი, რომლისკენაც მიისწრაფვის რიცხვი (1 + 1 / ნ) ნშეუზღუდავი ზრდით ნ(სმ. პირველი მშვენიერი ლიმიტიგვერდზე "რიცხვების თანმიმდევრობის ლიმიტები").
   რაც არ უნდა უცნაური იყოს, ბუნებრივი ლოგარითმები ძალიან მოსახერხებელი აღმოჩნდა ფუნქციების ანალიზთან დაკავშირებული სხვადასხვა ტიპის ოპერაციების შესრულებისას. ლოგარითმების გამოთვლა ფუძემდე ეგანხორციელდა ბევრად უფრო სწრაფად, ვიდრე ნებისმიერი სხვა მიზეზის გამო.

• რა არის საჭირო დღეს რუსეთში ბავშვის გასაშვილებლად? რუსეთში შვილად აყვანა, პასუხისმგებელი პირადი გადაწყვეტილების გარდა, მოიცავს კანდიდატების სახელმწიფო გადამოწმების მთელ რიგ პროცედურებს. მოსამზადებელ ეტაპზე მკაცრი შერჩევა ხელს უწყობს უფრო […]
• უფასო ინფორმაცია TIN ან OGRN-ის შესახებ საგადასახადო რეესტრიდან მთელ რუსეთში - ონლაინ ერთიანი საგადასახადო სერვისების პორტალზე, ინფორმაცია იურიდიული პირების სახელმწიფო რეგისტრაციის შესახებ, ინდივიდუალური მეწარმეები, […]
• საბუთების გარეშე მართვის სასჯელი (მძღოლის მოწმობა, დაზღვევა, სტს) ხანდახან დავიწყების გამო მძღოლები საჭეს უსაბუთოდ ჯდებიან და ჯარიმას იღებენ საბუთების გარეშე მართვისთვის. შეგახსენებთ, რომ ავტომოყვარულს მოეთხოვება […]
• ყვავილები მამაკაცებისთვის. რა ყვავილები შეგიძლიათ აჩუქოთ კაცს? რა ყვავილები შეგიძლიათ აჩუქოთ კაცს? "მამრობითი" ყვავილი ბევრი არ არის, მაგრამ არის ისეთებიც, რომლებსაც ჩუქნიან მამაკაცებს. პატარა ყვავილების სია თქვენს წინაშე: ქრიზანთემები. ვარდები. მიხაკები. […]
• შიდა მემორანდუმი არის დოკუმენტის სპეციალური ფორმა, რომელიც გამოიყენება საწარმოს შიდა გარემოში და ემსახურება წარმოების მიმდინარე პრობლემების სწრაფად მოგვარებას. როგორც წესი, ეს დოკუმენტი შედგენილია გარკვეული […]
• როდის და როგორ მიიღოთ თქვენი პენსიის დაფინანსებული ნაწილი სბერბანკიდან? Sberbank არის სახელმწიფო საპენსიო ფონდის პარტნიორი ბანკი. ამის საფუძველზე მოქალაქეებს, რომლებიც დარეგისტრირებულნი არიან დაგროვებითი პენსიაზე, შეუძლიათ გადარიცხონ დაფინანსებული ნაწილი […]
• ბავშვთა შეღავათები ულიანოვსკსა და ულიანოვსკის რეგიონში 2018 წელს გარდა ამისა, ფედერალური კანონმდებლობით დამტკიცებული პროგრამები მოქმედებს ყველა რეგიონში. ვნახოთ, ვის რა სარგებელის იმედი აქვს. როგორ რეგიონალური ხელისუფლება […]
• დეტალური ინსტრუქცია იმის შესახებ, თუ როგორ უნდა შედგეს მინდობილობა, რათა წარმოადგინოს ფიზიკური პირის ინტერესები სასამართლოში სამოქალაქო ან საარბიტრაჟო სარჩელში, ადმინისტრაციულ ან სისხლის სამართლის საქმეში, როგორც მოსარჩელის, ასევე მოპასუხის ინტერესები შეიძლება წარმოდგენილი იყოს ადვოკატის მიერ: […]

მოგეხსენებათ, გამონათქვამების ძალებით გამრავლებისას მათი მაჩვენებლები ყოველთვის იკრიბება (a b *a c = a b+c). ეს მათემატიკური კანონი გამოიტანა არქიმედესმა, მოგვიანებით კი, მე-8 საუკუნეში, მათემატიკოსმა ვირასენმა შექმნა მთელი რიცხვების მაჩვენებლების ცხრილი. სწორედ ისინი ემსახურებოდნენ ლოგარითმების შემდგომ აღმოჩენას. ამ ფუნქციის გამოყენების მაგალითები შეგიძლიათ ნახოთ თითქმის ყველგან, სადაც თქვენ უნდა გაამარტივოთ რთული გამრავლება მარტივი შეკრებით. თუ 10 წუთს დაუთმობთ ამ სტატიის კითხვას, ჩვენ აგიხსნით რა არის ლოგარითმები და როგორ იმუშაოთ მათთან. მარტივი და ხელმისაწვდომი ენით.

განმარტება მათემატიკაში

ლოგარითმი არის შემდეგი ფორმის გამოხატულება: log a b=c, ანუ ნებისმიერი არაუარყოფითი რიცხვის (ანუ ნებისმიერი დადებითი) ლოგარითმი "b" მის ფუძეზე "a" ითვლება "c" ხარისხად. ” რომელზედაც უნდა გაიზარდოს ფუძე “a”, რათა საბოლოოდ მივიღოთ მნიშვნელობა “b”. გავაანალიზოთ ლოგარითმი მაგალითების გამოყენებით, ვთქვათ არის გამონათქვამი log 2 8. როგორ მოვძებნოთ პასუხი? ეს ძალიან მარტივია, თქვენ უნდა იპოვოთ სიმძლავრე ისეთი, რომ 2-დან საჭირო სიმძლავრემდე მიიღოთ 8. თქვენს თავში გარკვეული გამოთვლების გაკეთების შემდეგ მივიღებთ რიცხვს 3! და ეს მართალია, რადგან 2 3-ის ხარისხზე იძლევა პასუხს, როგორც 8.

ლოგარითმების სახეები

ბევრი მოსწავლისა და სტუდენტისთვის ეს თემა რთული და გაუგებარი ჩანს, მაგრამ სინამდვილეში ლოგარითმები არც ისე საშინელია, მთავარია მათი ზოგადი მნიშვნელობის გაგება და მათი თვისებების და ზოგიერთი წესის დამახსოვრება. ლოგარითმული გამოსახულებების სამი განსხვავებული ტიპი არსებობს:

1. ბუნებრივი ლოგარითმი ln a, სადაც ფუძეა ეილერის რიცხვი (e = 2.7).
2. ათწილადი a, სადაც ფუძე არის 10.
3. ნებისმიერი b რიცხვის ლოგარითმი a>1-მდე.

თითოეული მათგანი წყდება სტანდარტული გზით, მათ შორის გამარტივება, შემცირება და შემდგომი შემცირება ერთ ლოგარითმზე ლოგარითმული თეორემების გამოყენებით. ლოგარითმების სწორი მნიშვნელობების მისაღებად, მათი ამოხსნისას უნდა გახსოვდეთ მათი თვისებები და მოქმედებების თანმიმდევრობა.

წესები და გარკვეული შეზღუდვები

მათემატიკაში არის რამდენიმე წესი-შეზღუდვა, რომლებიც მიღებულია აქსიომად, ანუ ისინი არ ექვემდებარება განხილვას და არის ჭეშმარიტება. მაგალითად, შეუძლებელია რიცხვების გაყოფა ნულზე და ასევე შეუძლებელია უარყოფითი რიცხვების ლუწი ფესვის ამოღება. ლოგარითმებს ასევე აქვთ საკუთარი წესები, რომელთა დაცვით შეგიძლიათ მარტივად ისწავლოთ მუშაობა გრძელი და ტევადი ლოგარითმული გამონათქვამებითაც კი:

• ფუძე "a" ყოველთვის უნდა იყოს ნულზე მეტი და არა 1-ის ტოლი, წინააღმდეგ შემთხვევაში გამოთქმა დაკარგავს თავის მნიშვნელობას, რადგან "1" და "0" ნებისმიერი ხარისხით ყოველთვის მათი მნიშვნელობების ტოლია;
• თუ a > 0, მაშინ a b >0, გამოდის, რომ „c“ ასევე უნდა იყოს ნულზე მეტი.

როგორ ამოხსნათ ლოგარითმები?

მაგალითად, დავალება მოცემულია პასუხის პოვნა განტოლებაზე 10 x = 100. ეს ძალიან მარტივია, თქვენ უნდა აირჩიოთ სიმძლავრე ათი რიცხვის აწევით, რომლითაც მივიღებთ 100-ს. ეს, რა თქმა უნდა, არის 10 2 = 100.

ახლა წარმოვიდგინოთ ეს გამონათქვამი ლოგარითმული ფორმით. ვიღებთ log 10 100 = 2. ლოგარითმების ამოხსნისას ყველა მოქმედება პრაქტიკულად იყრის თავს იმ სიმძლავრის საპოვნელად, რომელზედაც საჭიროა ლოგარითმის ფუძის შეყვანა მოცემული რიცხვის მისაღებად.

უცნობი ხარისხის მნიშვნელობის ზუსტად დასადგენად, თქვენ უნდა ისწავლოთ როგორ იმუშაოთ გრადუსების ცხრილთან. ეს ასე გამოიყურება:

როგორც ხედავთ, ზოგიერთი მაჩვენებლის გამოცნობა შესაძლებელია ინტუიციურად, თუ თქვენ გაქვთ ტექნიკური გონება და ცოდნა გამრავლების ცხრილის შესახებ. თუმცა, უფრო დიდი მნიშვნელობებისთვის დაგჭირდებათ დენის მაგიდა. მისი გამოყენება შეუძლიათ მათაც კი, ვინც საერთოდ არაფერი იცის რთული მათემატიკური თემების შესახებ. მარცხენა სვეტი შეიცავს რიცხვებს (ბაზა a), რიცხვების ზედა მწკრივი არის c სიმძლავრის მნიშვნელობა, რომელზედაც ამაღლებულია რიცხვი. კვეთაზე, უჯრედები შეიცავს ნომრის მნიშვნელობებს, რომლებიც პასუხია (a c =b). ავიღოთ, მაგალითად, პირველივე უჯრედი 10-ით და კვადრატში მივიღოთ მნიშვნელობა 100, რომელიც მითითებულია ჩვენი ორი უჯრედის გადაკვეთაზე. ყველაფერი ისეთი მარტივი და მარტივია, რომ ყველაზე ჭეშმარიტი ჰუმანისტიც კი მიხვდება!

განტოლებები და უტოლობა

გამოდის, რომ გარკვეულ პირობებში მაჩვენებლის მაჩვენებელი ლოგარითმია. აქედან გამომდინარე, ნებისმიერი მათემატიკური რიცხვითი გამონათქვამი შეიძლება დაიწეროს ლოგარითმული ტოლობის სახით. მაგალითად, 3 4 = 81 შეიძლება ჩაიწეროს, როგორც 81-ის მე-3 ლოგარითმი, რომელიც ტოლია ოთხს (log 3 81 = 4). უარყოფითი ძალებისთვის წესები იგივეა: 2 -5 = 1/32 ვწერთ ლოგარითმად, ვიღებთ log 2 (1/32) = -5. მათემატიკის ერთ-ერთი ყველაზე მომხიბვლელი განყოფილება არის "ლოგარითმების" თემა. განტოლებების მაგალითებსა და ამონახსნებს განვიხილავთ ქვემოთ, მათი თვისებების შესწავლისთანავე. ახლა ვნახოთ, როგორ გამოიყურება უტოლობები და როგორ განვასხვავოთ ისინი განტოლებისგან.

მოცემულია შემდეგი გამოთქმა: log 2 (x-1) > 3 - ეს არის ლოგარითმული უტოლობა, რადგან უცნობი მნიშვნელობა „x“ ლოგარითმული ნიშნის ქვეშ არის. და ასევე გამონათქვამში შედარებულია ორი სიდიდე: სასურველი რიცხვის ლოგარითმი ორზე მეტია სამზე.

ყველაზე მნიშვნელოვანი განსხვავება ლოგარითმულ განტოლებებსა და უტოლობას შორის არის ის, რომ განტოლებები ლოგარითმებით (მაგალითად, ლოგარითმი 2 x = √9) პასუხში გულისხმობს ერთ ან მეტ კონკრეტულ რიცხვობრივ მნიშვნელობას, ხოლო უტოლობის ამოხსნისას ორივე მისაღები დიაპაზონი. მნიშვნელობები და წერტილები განისაზღვრება ამ ფუნქციის დარღვევით. შედეგად, პასუხი არ არის ინდივიდუალური რიცხვების მარტივი ნაკრები, როგორც განტოლების პასუხში, არამედ უწყვეტი სერია ან რიცხვების სიმრავლე.

ძირითადი თეორემები ლოგარითმების შესახებ

ლოგარითმის მნიშვნელობების პოვნის პრიმიტიული ამოცანების გადაჭრისას, მისი თვისებები შეიძლება არ იყოს ცნობილი. თუმცა, როდესაც საქმე ეხება ლოგარითმულ განტოლებებს ან უტოლობას, უპირველეს ყოვლისა, აუცილებელია ლოგარითმების ყველა ძირითადი თვისების მკაფიოდ გაგება და პრაქტიკაში გამოყენება. განტოლებების მაგალითებს მოგვიანებით განვიხილავთ; ჯერ უფრო დეტალურად განვიხილოთ თითოეული თვისება.

1. ძირითადი იდენტურობა ასე გამოიყურება: a logaB =B. იგი გამოიყენება მხოლოდ მაშინ, როდესაც a მეტია 0-ზე, არ უდრის ერთს და B არის ნულზე მეტი.
2. პროდუქტის ლოგარითმი შეიძლება წარმოდგენილი იყოს შემდეგი ფორმულით: log d (s 1 * s 2) = log d s 1 + log d s 2. ამ შემთხვევაში სავალდებულო პირობაა: d, s 1 და s 2 > 0; a≠1. ამ ლოგარითმული ფორმულის მტკიცებულება შეგიძლიათ მაგალითებითა და ამოხსნით. მოდით log a s 1 = f 1 და log a s 2 = f 2, შემდეგ a f1 = s 1, a f2 = s 2. მივიღებთ, რომ s 1 * s 2 = a f1 *a f2 = a f1+f2 (თვისებები გრადუსი ), და შემდეგ განმარტებით: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, რაც დასამტკიცებლად იყო საჭირო.
3. კოეფიციენტის ლოგარითმი ასე გამოიყურება: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. ფორმულის სახით თეორემა იღებს შემდეგ ფორმას: log a q b n = n/q log a b.

ამ ფორმულას ეწოდება "ლოგარითმის ხარისხის თვისება". იგი წააგავს ჩვეულებრივი ხარისხების თვისებებს და გასაკვირი არ არის, რადგან ყველა მათემატიკა ემყარება ბუნებრივ პოსტულატებს. მოდით შევხედოთ მტკიცებულებას.

მოდით log a b = t, გამოდის t =b. თუ ორივე ნაწილს ავწევთ m ხარისხზე: a tn = b n;

მაგრამ რადგან a tn = (a q) nt/q = b n, ამიტომ log a q b n = (n*t)/t, მაშინ log a q b n = n/q log a b. თეორემა დადასტურდა.

პრობლემებისა და უთანასწორობის მაგალითები

ლოგარითმებზე ამოცანების ყველაზე გავრცელებული ტიპები არის განტოლებებისა და უტოლობების მაგალითები. ისინი გვხვდება თითქმის ყველა პრობლემურ წიგნში და ასევე არის მათემატიკის გამოცდების აუცილებელი ნაწილი. უნივერსიტეტში შესასვლელად ან მათემატიკაში მისაღები გამოცდების ჩასაბარებლად, თქვენ უნდა იცოდეთ როგორ სწორად ამოხსნათ ასეთი ამოცანები.

სამწუხაროდ, არ არსებობს ერთიანი გეგმა ან სქემა ლოგარითმის უცნობი მნიშვნელობის ამოხსნისა და განსაზღვრისთვის, მაგრამ გარკვეული წესები შეიძლება გამოყენებულ იქნას თითოეულ მათემატიკური უტოლობის ან ლოგარითმული განტოლებისთვის. უპირველეს ყოვლისა, თქვენ უნდა გაარკვიოთ, შეიძლება თუ არა გამოხატვის გამარტივება ან შემცირება ზოგად ფორმამდე. თქვენ შეგიძლიათ გაამარტივოთ გრძელი ლოგარითმული გამონათქვამები, თუ სწორად გამოიყენებთ მათ თვისებებს. მოდით გავეცნოთ მათ სწრაფად.

ლოგარითმული განტოლებების ამოხსნისას უნდა განვსაზღვროთ რა ტიპის ლოგარითმი გვაქვს: მაგალითის გამოხატულება შეიძლება შეიცავდეს ბუნებრივ ლოგარითმს ან ათობითი.

აქ არის მაგალითები ln100, ln1026. მათი გამოსავალი ემყარება იმ ფაქტს, რომ მათ უნდა დაადგინონ სიმძლავრე, რომლის ფუძე 10 ტოლი იქნება, შესაბამისად, 100 და 1026. ბუნებრივი ლოგარითმების ამოსახსნელად, თქვენ უნდა გამოიყენოთ ლოგარითმული იდენტობები ან მათი თვისებები. მოდით შევხედოთ სხვადასხვა ტიპის ლოგარითმული ამოცანების ამოხსნის მაგალითებს.

როგორ გამოვიყენოთ ლოგარითმის ფორმულები: მაგალითებითა და გადაწყვეტილებებით

ასე რომ, მოდით შევხედოთ ლოგარითმების შესახებ ძირითადი თეორემების გამოყენების მაგალითებს.

1. პროდუქტის ლოგარითმის თვისება შეიძლება გამოყენებულ იქნას ამოცანებში, სადაც აუცილებელია b რიცხვის დიდი მნიშვნელობის დაშლა უფრო მარტივ ფაქტორებად. მაგალითად, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. პასუხი არის 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1.5 - როგორც ხედავთ, ლოგარითმის სიმძლავრის მეოთხე თვისების გამოყენებით, ჩვენ მოვახერხეთ ერთი შეხედვით რთული და ამოუხსნელი გამოსახულების ამოხსნა. თქვენ უბრალოდ უნდა შეაფასოთ საფუძველი და შემდეგ ამოიღოთ მაჩვენებლების მნიშვნელობები ლოგარითმის ნიშნიდან.

დავალებები ერთიანი სახელმწიფო გამოცდიდან

ლოგარითმები ხშირად გვხვდება მისაღებ გამოცდებში, განსაკუთრებით ბევრი ლოგარითმული პრობლემა ერთიან სახელმწიფო გამოცდაში (სახელმწიფო გამოცდა სკოლის ყველა კურსდამთავრებულისთვის). როგორც წესი, ეს ამოცანები წარმოდგენილია არა მხოლოდ A ნაწილში (გამოცდის ყველაზე მარტივი ტესტი), არამედ C ნაწილში (ყველაზე რთული და მოცულობითი ამოცანები). გამოცდა მოითხოვს ზუსტ და სრულყოფილ ცოდნას თემის „ბუნებრივი ლოგარითმები“.

მაგალითები და პრობლემების გადაწყვეტა აღებულია ერთიანი სახელმწიფო გამოცდის ოფიციალური ვერსიებიდან. ვნახოთ, როგორ წყდება ასეთი ამოცანები.

მოცემული ჟურნალი 2 (2x-1) = 4. ამოხსნა:
მოდით გადავიწეროთ გამონათქვამი, გავამარტივოთ იგი ცოტა log 2 (2x-1) = 2 2, ლოგარითმის განმარტებით მივიღებთ, რომ 2x-1 = 2 4, შესაბამისად 2x = 17; x = 8.5.

• უმჯობესია, ყველა ლოგარითმი ერთსა და იმავე ფუძეზე შევიყვანოთ, რათა გამოსავალი არ იყოს რთული და დამაბნეველი.
• ლოგარითმის ნიშნის ქვეშ მყოფი ყველა გამონათქვამი მითითებულია, როგორც დადებითი, ამიტომ, როდესაც გამოხატვის გამოხატულება, რომელიც არის ლოგარითმის ნიშნის ქვეშ და მისი ფუძე ამოღებულია მულტიპლიკატორად, ლოგარითმის ქვეშ დარჩენილი გამოხატულება უნდა იყოს დადებითი.

გამომდინარეობს მისი განმარტებიდან. ასე რომ, რიცხვის ლოგარითმი ბდაფუძნებული აგანისაზღვრება, როგორც მაჩვენებელი, რომელზეც რიცხვი უნდა გაიზარდოს ანომრის მისაღებად ბ(ლოგარითმი არსებობს მხოლოდ დადებითი რიცხვებისთვის).

ამ ფორმულირებიდან გამომდინარეობს, რომ გაანგარიშება x=log a b, უდრის განტოლების ამოხსნას a x =b.Მაგალითად, ჟურნალი 2 8 = 3რადგან 8 = 2 3 . ლოგარითმის ფორმულირება იძლევა იმის დასაბუთებას, რომ თუ b=a გ, შემდეგ რიცხვის ლოგარითმი ბდაფუძნებული აუდრის თან. ასევე ნათელია, რომ ლოგარითმების თემა მჭიდრო კავშირშია რიცხვის ხარისხების თემასთან.

ლოგარითმებით, როგორც ნებისმიერი რიცხვით, შეგიძლიათ ამის გაკეთება შეკრების, გამოკლების ოპერაციებიდა გარდაიქმნება ყველა შესაძლო გზით. მაგრამ იმის გამო, რომ ლოგარითმები არ არის სრულიად ჩვეულებრივი რიცხვები, აქ მოქმედებს მათი სპეციალური წესები, რომლებიც ე.წ. ძირითადი თვისებები.

ლოგარითმების შეკრება და გამოკლება.

ავიღოთ ორი ლოგარითმი ერთი და იგივე ფუძეებით: შესვლა xდა შესვლა y. შემდეგ შესაძლებელია შეკრებისა და გამოკლების ოპერაციების შესრულება:

log a x+ log a y= log a (x·y);

log a x - log a y = log a (x:y).

ჟურნალი ა(x 1 . x 2 . x 3 ... x k) = შესვლა x 1 + შესვლა x 2 + შესვლა x 3 + ... + log a x k.

დან ლოგარითმის კოეფიციენტის თეორემაშეიძლება მივიღოთ ლოგარითმის კიდევ ერთი თვისება. საყოველთაოდ ცნობილია, რომ ჟურნალი ა 1 = 0, შესაბამისად

ჟურნალი ა 1 /ბ= ჟურნალი ა 1 - ჟურნალი ბ= -ლოგი ბ.

ეს ნიშნავს, რომ არსებობს თანასწორობა:

log a 1 / b = - log a b.

ორი საპასუხო რიცხვის ლოგარითმებიამავე მიზეზით განსხვავდებიან ერთმანეთისაგან მხოლოდ ნიშნით. Ისე:

ჟურნალი 3 9= - ჟურნალი 3 1 / 9 ; log 5 1 / 125 = -log 5 125.

(ბერძნული λόγος - "სიტყვა", "კავშირი" და ἀριθμός - "რიცხვი") რიცხვები ბდაფუძნებული ა(log α ბ) ეწოდება ასეთ რიცხვს გ, და ბ= გ, ანუ ჩანაწერების ჟურნალი α ბ=გდა b=aგექვივალენტები არიან. ლოგარითმი აზრი აქვს, თუ a > 0, a ≠ 1, b > 0.

Სხვა სიტყვებით ლოგარითმინომრები ბდაფუძნებული აჩამოყალიბებულია მაჩვენებლის სახით, რომელზეც რიცხვი უნდა გაიზარდოს ანომრის მისაღებად ბ(ლოგარითმი არსებობს მხოლოდ დადებითი რიცხვებისთვის).

ამ ფორმულირებიდან გამომდინარეობს, რომ გაანგარიშება x= log α ბ, უდრის a x =b განტოლების ამოხსნის.

Მაგალითად:

ჟურნალი 2 8 = 3, რადგან 8 = 2 3.

ხაზგასმით აღვნიშნოთ, რომ ლოგარითმის მითითებული ფორმულირება შესაძლებელს ხდის დაუყოვნებლივ განსაზღვროს ლოგარითმის მნიშვნელობა, როდესაც რიცხვი ლოგარითმის ნიშნის ქვეშ მოქმედებს როგორც ფუძის გარკვეული ძალა. მართლაც, ლოგარითმის ფორმულირება იძლევა იმის დასაბუთებას, რომ თუ b=a გ, შემდეგ რიცხვის ლოგარითმი ბდაფუძნებული აუდრის თან. ასევე ნათელია, რომ ლოგარითმების თემა მჭიდრო კავშირშია თემასთან რიცხვის ძალა.

ლოგარითმის გამოთვლა ეწოდება ლოგარითმი. ლოგარითმი არის ლოგარითმის აღების მათემატიკური ოპერაცია. ლოგარითმების აღებისას ფაქტორების პროდუქტები გარდაიქმნება ტერმინების ჯამებად.

გაძლიერებაარის ლოგარითმის შებრუნებული მათემატიკური მოქმედება. პოტენციაციის დროს მოცემული ბაზა ამაღლებულია გამოხატვის ხარისხამდე, რომელზედაც ხდება პოტენციაცია. ამ შემთხვევაში ტერმინების ჯამები გარდაიქმნება ფაქტორების ნამრავლად.

საკმაოდ ხშირად, რეალური ლოგარითმები გამოიყენება ბაზებით 2 (ორობითი), ეილერის რიცხვი e ≈ 2.718 (ბუნებრივი ლოგარითმი) და 10 (ათწილადი).

ამ ეტაპზე მიზანშეწონილია განიხილოს ლოგარითმის ნიმუშებიჟურნალი 7 2 , ლნ √ 5, lg0.0001.

ხოლო ჩანაწერებს lg(-3), log -3 3.2, log -1 -4.3 აზრი არ აქვს, რადგან პირველში უარყოფითი რიცხვია მოთავსებული ლოგარითმის ნიშნის ქვეშ, მეორეში არის უარყოფითი რიცხვი. ფუძეში, ხოლო მესამეში არის უარყოფითი რიცხვი ლოგარითმის ნიშნის ქვეშ და ერთეული ბაზაზე.

ლოგარითმის განსაზღვრის პირობები.

ცალკე უნდა განვიხილოთ პირობები a > 0, a ≠ 1, b > 0.რომლებითაც მივიღებთ ლოგარითმის განმარტება.მოდით განვიხილოთ, რატომ იქნა მიღებული ეს შეზღუდვები. ამაში დაგვეხმარება x = log α ფორმის ტოლობა ბ, რომელსაც ეწოდება ძირითადი ლოგარითმული იდენტობა, რომელიც პირდაპირ გამომდინარეობს ზემოთ მოცემული ლოგარითმის განმარტებიდან.

ავიღოთ პირობა a≠1. ვინაიდან ერთი ნებისმიერი სიმძლავრის მიმართ უდრის ერთს, მაშინ ტოლობა x=log α ბშეიძლება არსებობდეს მხოლოდ მაშინ, როცა b=1, მაგრამ ჟურნალი 1 1 იქნება ნებისმიერი რეალური რიცხვი. ამ გაურკვევლობის აღმოსაფხვრელად, ჩვენ ვიღებთ a≠1.

დავამტკიცოთ პირობის აუცილებლობა a>0. ზე a=0ლოგარითმის ფორმულირების მიხედვით შეიძლება არსებობდეს მხოლოდ მაშინ, როცა b=0. და შესაბამისად მაშინ ჟურნალი 0 0შეიძლება იყოს ნებისმიერი არანულოვანი რეალური რიცხვი, ვინაიდან ნული ნებისმიერ არანულოვან ხარისხზე არის ნული. ეს გაურკვევლობა შეიძლება აღმოიფხვრას მდგომარეობით a≠0. Და როცა ა<0 ჩვენ უნდა უარვყოთ ლოგარითმის რაციონალური და ირაციონალური მნიშვნელობების ანალიზი, რადგან რაციონალური და ირაციონალური მაჩვენებლის მქონე ხარისხი განისაზღვრება მხოლოდ არაუარყოფითი ბაზებისთვის. სწორედ ამ მიზეზით არის გათვალისწინებული პირობა a>0.

და ბოლო პირობა b>0გამომდინარეობს უთანასწორობიდან a>0, ვინაიდან x=log α ბ, და ხარისხის მნიშვნელობა დადებითი ბაზით აყოველთვის პოზიტიური.

ლოგარითმების მახასიათებლები.

ლოგარითმებიხასიათდება გამორჩეული მახასიათებლები, რამაც გამოიწვია მათი ფართო გამოყენება მტკივნეული გამოთვლების საგრძნობლად გასაადვილებლად. "ლოგარითმების სამყაროში" გადასვლისას, გამრავლება გარდაიქმნება ბევრად უფრო მარტივ მიმატებად, გაყოფა გარდაიქმნება გამოკლებად, ხოლო სიმძლავრე და ფესვის ამოღება გარდაიქმნება, შესაბამისად, გამრავლებად და გაყოფად მაჩვენებლით.

ლოგარითმების ფორმულირება და მათი მნიშვნელობების ცხრილი (ტრიგონომეტრიული ფუნქციებისთვის) პირველად გამოქვეყნდა 1614 წელს შოტლანდიელმა მათემატიკოსმა ჯონ ნაპიერმა. ლოგარითმული ცხრილები, გაფართოებული და დეტალური სხვა მეცნიერების მიერ, ფართოდ გამოიყენებოდა სამეცნიერო და საინჟინრო გამოთვლებში და აქტუალური დარჩა ელექტრონული კალკულატორებისა და კომპიუტერების გამოყენებამდე.