მოცემული f ფუნქციის წარმოებულის პოვნა ეწოდება. e-ს წარმოებული x სიმძლავრე და ექსპონენციალური ფუნქცია

ამ გაკვეთილზე ვისწავლით დიფერენცირების ფორმულებისა და წესების გამოყენებას.

მაგალითები. იპოვნეთ ფუნქციების წარმოებულები.

1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. წესის გამოყენება მე, ფორმულები 4, 2 და 1. ჩვენ ვიღებთ:

y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.

2. y=3x 6 -2x+5. ჩვენ ვხსნით ანალოგიურად, იგივე ფორმულებისა და ფორმულის გამოყენებით 3.

y’=3∙6x 5 -2=18x 5 -2.

წესის გამოყენება მე, ფორმულები 3, 5 და 6 და 1.

წესის გამოყენება IV, ფორმულები 5 და 1 .

მეხუთე მაგალითში წესის მიხედვით მეჯამის წარმოებული უდრის წარმოებულთა ჯამს და ჩვენ ახლახან ვიპოვეთ 1-ლი წევრის წარმოებული (მაგალითი 4 ), შესაბამისად, ჩვენ ვიპოვით წარმოებულებს მე-2და მე-3პირობები და 1-ლისთვისშეჯამება შეგვიძლია დაუყოვნებლივ დავწეროთ შედეგი.

განვასხვავოთ მე-2და მე-3ტერმინები ფორმულის მიხედვით 4 . ამისათვის ჩვენ ვაქცევთ მესამე და მეოთხე ხარისხების ფესვებს მნიშვნელებში უარყოფითი მაჩვენებლების მქონე ძალებად და შემდეგ, შესაბამისად 4 ფორმულა, ჩვენ ვპოულობთ ძალაუფლების წარმოებულებს.

შეხედეთ ამ მაგალითს და შედეგს. დაიჭირე ნიმუში? ჯარიმა. ეს ნიშნავს, რომ ჩვენ გვაქვს ახალი ფორმულა და შეგვიძლია დავამატოთ ის ჩვენს წარმოებულთა ცხრილში.

გადავწყვიტოთ მეექვსე მაგალითი და გამოვიტანოთ სხვა ფორმულა.

გამოვიყენოთ წესი IVდა ფორმულა 4 . შევამციროთ მიღებული წილადები.

მოდით შევხედოთ ამ ფუნქციას და მის წარმოებულს. თქვენ, რა თქმა უნდა, გესმით ნიმუში და მზად ხართ დაასახელოთ ფორმულა:

ისწავლეთ ახალი ფორმულები!

მაგალითები.

1. იპოვეთ არგუმენტის ზრდა და y= ფუნქციის ზრდა x 2, თუ არგუმენტის საწყისი მნიშვნელობა ტოლი იყო 4 და ახალი - 4,01 .

გამოსავალი.

ახალი არგუმენტის მნიშვნელობა x=x 0 +Δx. ჩავანაცვლოთ მონაცემები: 4.01=4+Δх, შესაბამისად არგუმენტის ზრდა Δх=4.01-4=0.01. ფუნქციის ზრდა, განსაზღვრებით, უდრის სხვაობას ფუნქციის ახალ და წინა მნიშვნელობებს შორის, ე.ი. Δy=f (x 0 +Δx) - f (x 0). რადგან გვაქვს ფუნქცია y=x2, ეს ორ=(x 0 +Δx) 2 - (x 0) 2 =(x 0) 2 +2x 0 · Δx+(Δx) 2 - (x 0) 2 =2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

პასუხი: არგუმენტის ზრდა Δх=0.01; ფუნქციის ზრდა ორ=0,0801.

ფუნქციის ზრდა შეიძლება განსხვავებულად მოიძებნოს: Δy=y (x 0 +Δx) -y (x 0)=y(4.01) -y(4)=4.01 2 -4 2 =16.0801-16=0.0801.

2. იპოვეთ ფუნქციის გრაფიკზე ტანგენსის დახრის კუთხე y=f(x)წერტილში x 0, თუ f" (x 0) = 1.

გამოსავალი.

წარმოებულის მნიშვნელობა ტანგენციის წერტილში x 0და არის ტანგენტის კუთხის ტანგენტის მნიშვნელობა (წარმოებულის გეომეტრიული მნიშვნელობა). Ჩვენ გვაქვს: f "(x 0) = tanα = 1 → α = 45°,რადგან tg45°=1.

პასუხი: ამ ფუნქციის გრაფიკზე ტანგენსი ქმნის კუთხეს Ox ღერძის დადებითი მიმართულებით ტოლი 45°.

3. გამოიღეთ ფუნქციის წარმოებულის ფორმულა y=xn.

დიფერენციაციაარის ფუნქციის წარმოებულის პოვნის მოქმედება.

წარმოებულების პოვნისას გამოიყენეთ ფორმულები, რომლებიც მიღებული იქნა წარმოებულის განმარტების საფუძველზე, ისევე, როგორც ჩვენ გამოვიყვანეთ წარმოებული ხარისხის ფორმულა: (x n)" = nx n-1.

ეს არის ფორმულები.

წარმოებულების ცხრილიუფრო ადვილი იქნება დამახსოვრება სიტყვიერი ფორმულირებების წარმოთქმით:

1. მუდმივი სიდიდის წარმოებული არის ნული.

2. X მარტივი უდრის ერთი.

3. მუდმივი ფაქტორი შეიძლება ამოღებულ იქნას წარმოებულის ნიშნიდან.

4. ხარისხის წარმოებული უდრის ამ ხარისხის მაჩვენებლის ნამრავლს იმავე ფუძის მქონე გრადუსით, მაგრამ მაჩვენებელი ერთით ნაკლებია.

5. ფესვის წარმოებული ტოლია ერთი გაყოფილი ორ თანაბარ ფესვზე.

6. ერთის წარმოებული გაყოფილი x-ზე ტოლია მინუს ერთი გაყოფილი x კვადრატზე.

7. სინუსის წარმოებული ტოლია კოსინუსის.

8. კოსინუსის წარმოებული უდრის მინუს სინუსს.

9. ტანგენსის წარმოებული ტოლია ერთის გაყოფილი კოსინუსის კვადრატზე.

10. კოტანგენტის წარმოებული უდრის მინუს ერთი გაყოფილი სინუსის კვადრატზე.

ჩვენ ვასწავლით დიფერენციაციის წესები.

1. ალგებრული ჯამის წარმოებული ტოლია ტერმინების წარმოებულების ალგებრული ჯამის.

2. პროდუქტის წარმოებული უდრის პირველი ფაქტორის წარმოებულის ნამრავლს და მეორეს პლუს პირველი ფაქტორისა და მეორეს წარმოებულის ნამრავლს.

3. "y"-ის წარმოებული გაყოფილი "ve"-ზე ტოლია წილადისა, რომელშიც მრიცხველი არის "y მარტივი გამრავლებული "ve"-ზე გამოკლებული "y გამრავლებული ve Prime-ზე", ხოლო მნიშვნელი არის "ve კვადრატი".

4. ფორმულის განსაკუთრებული შემთხვევა 3.

ვისწავლოთ ერთად!

გვერდი 1 სულ 1 1

გეომეტრიის, მექანიკის, ფიზიკის და ცოდნის სხვა დარგების სხვადასხვა ამოცანების გადაჭრისას, გაჩნდა საჭიროება ამ ფუნქციიდან იგივე ანალიტიკური პროცესის გამოყენებით. y=f(x)მიიღეთ ახალი ფუნქცია ე.წ წარმოებული ფუნქცია(ან უბრალოდ წარმოებული) მოცემული ფუნქციის f(x)და აღინიშნება სიმბოლოთი

პროცესი, რომლითაც მოცემული ფუნქციიდან f(x)მიიღეთ ახალი ფუნქცია f" (x), დაურეკა დიფერენციაციადა შედგება შემდეგი სამი ეტაპისგან: 1) არგუმენტის მიცემა xმატება  xდა განსაზღვრეთ ფუნქციის შესაბამისი ზრდა  y = f(x+ x) -f(x); 2) შეადგინეთ ურთიერთობა

3) დათვლა xმუდმივი და  x0, ვპოულობთ
, რომელსაც ჩვენ აღვნიშნავთ f" (x), თითქოს ხაზს უსვამს, რომ მიღებული ფუნქცია დამოკიდებულია მხოლოდ მნიშვნელობაზე x, რაზეც მივდივართ ლიმიტამდე. განმარტება: წარმოებული y "=f" (x) მოცემული ფუნქცია y=f(x) მოცემული x-ისთვისეწოდება ფუნქციის ზრდის შეფარდების ზღვარი არგუმენტის ზრდასთან, იმ პირობით, რომ არგუმენტის ზრდა ნულისკენ მიისწრაფვის, თუ, რა თქმა უნდა, ეს ზღვარი არსებობს, ე.ი. სასრული. ამრიგად,
, ან

გაითვალისწინეთ, რომ თუ გარკვეული მნიშვნელობისთვის xმაგალითად, როდესაც x=a, დამოკიდებულება
ზე  x0 არ მიდრეკილია სასრულ ზღვრამდე, მაშინ ამ შემთხვევაში ამბობენ, რომ ფუნქცია f(x)ზე x=a(ან წერტილში x=a) არ აქვს წარმოებული ან არ არის დიფერენცირებადი წერტილში x=a.

2. წარმოებულის გეომეტრიული მნიშვნელობა.

განვიხილოთ y = f (x) ფუნქციის გრაფიკი, დიფერენცირებადი x 0 წერტილის სიახლოვეს.

f(x)

განვიხილოთ თვითნებური სწორი ხაზი, რომელიც გადის ფუნქციის გრაფიკის წერტილში - წერტილი A(x 0, f (x 0)) და კვეთს გრაფიკს რაღაც წერტილში B(x;f(x)). ასეთ ხაზს (AB) სეკანტი ეწოდება. ∆ABC-დან: AC = ∆x; ВС =∆у; tgβ=∆y/∆x.

AC || Ox, შემდეგ ALO = BAC = β (როგორც შესაბამისი პარალელისთვის). მაგრამ ALO არის AB სეკანტის დახრის კუთხე Ox ღერძის დადებითი მიმართულების მიმართ. ეს ნიშნავს, რომ tanβ = k არის AB სწორი ხაზის დახრილობა.

ახლა შევამცირებთ ∆x, ე.ი. ∆х→ 0. ამ შემთხვევაში B წერტილი გრაფიკის მიხედვით მიახლოვდება A წერტილს და ბრუნავს სეკანტი AB. AB სეკანტის შემზღუდველი პოზიცია ∆x→ 0-ზე იქნება სწორი ხაზი (a), რომელსაც ეწოდება tangent y = f (x) ფუნქციის გრაფიკზე A წერტილში.

თუ ზღვარზე გადავალთ, როგორც ∆x → 0 ტოლობაში tgβ =∆y/∆x, მივიღებთ
ortg =f "(x 0), ვინაიდან
-ოქსის ღერძის დადებითი მიმართულების ტანგენსის დახრის კუთხე
, წარმოებულის განმარტებით. მაგრამ tg = k არის ტანგენტის კუთხური კოეფიციენტი, რაც ნიშნავს k = tg = f "(x 0).

ასე რომ, წარმოებულის გეომეტრიული მნიშვნელობა შემდეგია:

x წერტილში ფუნქციის წარმოებული 0 x აბსცისით დახატული ფუნქციის გრაფიკზე ტანგენსის დახრილობის ტოლია 0 .

3. წარმოებულის ფიზიკური მნიშვნელობა.

განვიხილოთ წერტილის მოძრაობა სწორი ხაზის გასწვრივ. მოცემული იყოს წერტილის კოორდინატი ნებისმიერ დროს x(t). ცნობილია (ფიზიკის კურსიდან), რომ საშუალო სიჩქარე დროის მონაკვეთში ტოლია დროის ამ მონაკვეთში გავლილი მანძილის თანაფარდობასთან, ე.ი.

Vav = ∆x/∆t. გადავიდეთ ბოლო ტოლობის ზღვარზე, როგორც ∆t → 0.

lim Vav (t) = (t 0) - მყისიერი სიჩქარე დროს t 0, ∆t → 0.

და lim = ∆x/∆t = x"(t 0) (წარმოებულის განმარტებით).

ასე რომ, (t) =x"(t).

წარმოებულის ფიზიკური მნიშვნელობა ასეთია: ფუნქციის წარმოებულიწ = ვ(x) წერტილშიx 0 არის ფუნქციის ცვლილების სიჩქარევ(x) წერტილშიx 0

წარმოებული გამოიყენება ფიზიკაში სიჩქარის საპოვნელად კოორდინატების ცნობილი ფუნქციიდან დროის წინააღმდეგ, აჩქარება სიჩქარის ცნობილი ფუნქციიდან დროის წინააღმდეგ.

(t) = x"(t) - სიჩქარე,

a(f) = "(t) - აჩქარება, ან

თუ წრეში მატერიალური წერტილის მოძრაობის კანონი ცნობილია, მაშინ შეიძლება ვიპოვოთ კუთხური სიჩქარე და კუთხური აჩქარება ბრუნვის დროს:

φ = φ(t) - კუთხის ცვლილება დროთა განმავლობაში,

ω = φ"(t) - კუთხური სიჩქარე,

ε = φ"(t) - კუთხოვანი აჩქარება, ან ε = φ"(t).

თუ ცნობილია არაერთგვაროვანი ღეროს მასის განაწილების კანონი, მაშინ შეიძლება მოიძებნოს არაჰომოგენური ღეროს წრფივი სიმკვრივე:

m = m(x) - მასა,

x , l - ღეროს სიგრძე,

p = m"(x) - წრფივი სიმკვრივე.

წარმოებულის გამოყენებით იხსნება ამოცანები ელასტიურობის თეორიიდან და ჰარმონიული ვიბრაციებიდან. ასე რომ, ჰუკის კანონის მიხედვით

F = -kx, x – ცვლადი კოორდინატი, k – ზამბარის ელასტიურობის კოეფიციენტი. თუ დავსვამთ ω 2 =k/m, ვიღებთ ზამბარის ქანქარის დიფერენციალურ განტოლებას x"(t) + ω 2 x(t) = 0,

სადაც ω = √k/√m რხევის სიხშირე (l/c), k - ზამბარის სიმტკიცე (H/m).

y" + ω 2 y = 0 ფორმის განტოლებას ეწოდება ჰარმონიული რხევების (მექანიკური, ელექტრული, ელექტრომაგნიტური) განტოლება. ასეთი განტოლებების ამოხსნა არის ფუნქცია.

y = Asin(ωt + φ 0) ან y = Acos(ωt + φ 0), სადაც

A - რხევების ამპლიტუდა, ω - ციკლური სიხშირე,

φ 0 - საწყისი ფაზა.

გაკვეთილი თემაზე: "რა არის წარმოებული? წარმოებულის განმარტება"

დამატებითი მასალები
ძვირფასო მომხმარებლებო, არ დაგავიწყდეთ დატოვოთ თქვენი კომენტარები, მიმოხილვები, სურვილები! ყველა მასალა შემოწმებულია ანტივირუსული პროგრამით.

სასწავლო საშუალებები და ტრენაჟორები ინტეგრალის ონლაინ მაღაზიაში მე-10 კლასისთვის
ალგებრული ამოცანები პარამეტრებთან, 9–11 კლასები
პროგრამული გარემო "1C: მათემატიკური კონსტრუქტორი 6.1"

რას შევისწავლით:
1. წარმოებულის ცნების შესავალი.
2. პატარა ისტორია.

4. წარმოებული ფუნქციის გრაფიკზე. წარმოებულის გეომეტრიული მნიშვნელობა.

6. ფუნქციის დიფერენციაცია.
7. მაგალითები.

წარმოებულის ცნების შესავალი

ბევრი პრობლემაა, რომლებიც მნიშვნელობით სრულიად განსხვავებულია, მაგრამ არსებობს მათემატიკური მოდელები, რომლებიც საშუალებას გვაძლევს გამოვთვალოთ ჩვენი ამოცანების გადაწყვეტილებები ზუსტად იმავე გზით. მაგალითად, თუ განვიხილავთ დავალებებს, როგორიცაა:

ა) არის საბანკო ანგარიში, რომელიც მუდმივად იცვლება რამდენიმე დღეში ერთხელ, თანხა მუდმივად იზრდება, უნდა მოძებნოთ რა სიჩქარით იზრდება ანგარიში.
ბ) ქარხანა აწარმოებს კანფეტებს, არის გარკვეული მუდმივი მატება კანფეტების გამომუშავებაში, გაიგეთ რამდენად სწრაფად იზრდება კანფეტების მატება.
გ) მანქანის სიჩქარე t დროის გარკვეულ მომენტში, თუ მანქანის მდებარეობა ცნობილია და ის მოძრაობს სწორი ხაზით.
დ) გვეძლევა ფუნქციის გრაფიკი და რაღაც მომენტში მასზე ტანგენსი იხატება, უნდა ვიპოვოთ ტანგენსზე დახრილობის კუთხის ტანგენსი.
ჩვენი ამოცანების ფორმულირება სრულიად განსხვავებულია და, როგორც ჩანს, ისინი სულ სხვაგვარად წყდება, მაგრამ მათემატიკოსებმა გაარკვიეს, თუ როგორ უნდა ამოხსნან ყველა ეს პრობლემა ზუსტად ერთნაირად. შემოიღეს წარმოებულის ცნება.

ცოტა ისტორია

ტერმინი წარმოებული შემოიღო დიდმა მათემატიკოსმა ლაგრანჟმა, რუსულად თარგმანი მიღებულია ფრანგული სიტყვიდან derivee და მან ასევე შემოიღო წარმოებულის თანამედროვე აღნიშვნა, რომელსაც მოგვიანებით განვიხილავთ.
ლაიბნიცმა და ნიუტონმა განიხილეს წარმოებულის ცნება თავიანთ ნაშრომებში; მათ აღმოაჩინეს ჩვენი ტერმინის გამოყენება გეომეტრიასა და მექანიკაში, შესაბამისად.
ცოტა მოგვიანებით გავიგებთ, რომ წარმოებული განისაზღვრება ლიმიტის მეშვეობით, მაგრამ მათემატიკის ისტორიაში მცირე პარადოქსია. მათემატიკოსებმა ისწავლეს წარმოებულის გამოთვლა, სანამ ლიმიტის ცნებას შემოიტანდნენ და რეალურად გაიგეს რა არის წარმოებული.

დაე, ფუნქცია y=f(x) განისაზღვროს გარკვეულ ინტერვალზე, რომელიც შეიცავს გარკვეულ x0 წერტილს. Δx არგუმენტის ზრდა არ ტოვებს ჩვენს ინტერვალს. ვიპოვოთ ნამატი Δy და შევადგინოთ შეფარდება Δy/Δx; თუ ამ შეფარდებას აქვს ზღვარი, რადგან Δx მიდრეკილია ნულისკენ, მაშინ ამ ზღვარს ეწოდება y=f(x) ფუნქციის წარმოებული x0 წერტილში და აღინიშნება. f'(x0).

შევეცადოთ ავხსნათ რა არის წარმოებული არამათემატიკურ ენაზე:
მათემატიკური ენაში: წარმოებული არის ფუნქციის ზრდის შეფარდების ზღვარი მისი არგუმენტის ზრდასთან, როდესაც არგუმენტის ზრდა ნულისკენ მიისწრაფვის.
ჩვეულებრივ ენაში: წარმოებული არის ფუნქციის ცვლილების სიჩქარე x0 წერტილში.
მოდით შევხედოთ სამი ფუნქციის გრაფიკებს:

ბიჭებო, როგორ ფიქრობთ, რომელი მრუდი იზრდება უფრო სწრაფად?
პასუხი ყველასთვის აშკარა ჩანს: 1 მრუდი უფრო სწრაფად იზრდება, ვიდრე სხვები. ჩვენ ვუყურებთ, თუ რამდენად ციცაბო მაღლდება ფუნქციის გრაფიკი. სხვა სიტყვებით რომ ვთქვათ, რამდენად სწრაფად იცვლება ორდინატი x-ის ცვლილებისას. ერთსა და იმავე ფუნქციას სხვადასხვა წერტილში შეიძლება ჰქონდეს განსხვავებული წარმოებული მნიშვნელობები - ანუ ის შეიძლება შეიცვალოს უფრო სწრაფად ან ნელა.

წარმოებული ფუნქციის გრაფიკზე. წარმოებულის გეომეტრიული მნიშვნელობა

ახლა ვნახოთ, როგორ ვიპოვოთ წარმოებული ფუნქციის გრაფიკების გამოყენებით:


ვნახოთ ფუნქციის ჩვენი გრაფიკი: დავხატოთ ფუნქციის გრაფიკის ტანგენსი x0 აბსცისით. ტანგენტის ხაზი და ჩვენი ფუნქციის გრაფიკი ეხება A წერტილს. ჩვენ უნდა შევაფასოთ, რამდენად ციცაბო მაღლა დგება ფუნქციის გრაფიკი. ამისათვის მოსახერხებელი მნიშვნელობა არის ტანგენტის კუთხის ტანგენსი.

განმარტება. x0 წერტილში ფუნქციის წარმოებული ტოლია ამ წერტილში ფუნქციის გრაფიკზე დახატული ტანგენსის კუთხის ტანგენტისა.

ტანგენტის კუთხე არჩეულია, როგორც კუთხე ტანგენტსა და x-ღერძის დადებით მიმართულებას შორის.
ასე რომ, ჩვენი ფუნქციის წარმოებული უდრის:

ასე რომ, წარმოებული x0 წერტილში ტოლია ტანგენტის კუთხის ტანგენტს, ეს არის წარმოებულის გეომეტრიული მნიშვნელობა.

y=f(x) ფუნქციის წარმოებულის პოვნის ალგორითმი.
ა) დააფიქსირეთ x-ის მნიშვნელობა, იპოვეთ f(x).
ბ) იპოვეთ x+ Δx არგუმენტის ნამატი და f(x+ Δx) ფუნქციის ნაზრდის მნიშვნელობა.
გ) იპოვეთ Δy= f(x+ Δx)-f(x) ფუნქციის ნამატი.
დ) შეადგინეთ თანაფარდობა: Δy/Δx
დ) გამოთვალეთ

ეს არის ჩვენი ფუნქციის წარმოებული.

ფუნქციის დიფერენციაცია

თუ ფუნქციას y=f(x) აქვს წარმოებული x წერტილში, მაშინ მას ეწოდება დიფერენცირებადი x წერტილში. წარმოებულის პოვნის პროცესს ეწოდება y=f(x) ფუნქციის დიფერენციაცია.
დავუბრუნდეთ ფუნქციის უწყვეტობის საკითხს. თუ ფუნქცია გარკვეულ წერტილში დიფერენცირებადია, მაშინ ტანგენსი შეიძლება დაიხაზოს ფუნქციის გრაფიკზე ამ წერტილში; ფუნქციას არ შეიძლება ჰქონდეს უწყვეტობა ამ ეტაპზე, მაშინ ტანგენსი უბრალოდ არ შეიძლება დახატოს.
ასე რომ, ჩვენ ჩამოვწერთ ზემოთ მოცემულ განმარტებას:
განმარტება. თუ ფუნქცია დიფერენცირებადია x წერტილში, მაშინ ის უწყვეტია ამ წერტილში.
თუმცა, თუ ფუნქცია არის უწყვეტი წერტილში, ეს არ ნიშნავს, რომ ის ამ წერტილში დიფერენცირებადია. მაგალითად, ფუნქცია y=|x| x=0 წერტილში არის უწყვეტი, მაგრამ ტანგენსი არ არის დახატული, რაც ნიშნავს, რომ წარმოებული არ არსებობს.

წარმოებულის მაგალითები

იპოვეთ ფუნქციის წარმოებული: y=3x
გამოსავალი:
ჩვენ გამოვიყენებთ წარმოებული ძიების ალგორითმს.
1) x-ის ფიქსირებული მნიშვნელობისთვის ფუნქციის მნიშვნელობა y=3x
2) x+ Δx წერტილში, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) იპოვეთ ფუნქციის ნამატი: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δ

წარმოებული არის ყველაზე მნიშვნელოვანი ცნება მათემატიკური ანალიზში. იგი ახასიათებს არგუმენტის ფუნქციის ცვლილებას xრაღაც მომენტში. უფრო მეტიც, წარმოებული თავად არის არგუმენტის ფუნქცია x

ფუნქციის წარმოებული წერტილში არის ფუნქციის ზრდის შეფარდების ზღვარი (თუ ის არსებობს და სასრულია) არგუმენტის ზრდასთან, იმ პირობით, რომ ეს უკანასკნელი ნულისკენ მიისწრაფვის.

ყველაზე ხშირად გამოიყენება შემდეგი წარმოებული აღნიშვნა :

მაგალითი 1.უპირატესობის მიღება წარმოებულის განმარტებაიპოვნეთ ფუნქციის წარმოებული

გამოსავალი. წარმოებულის განმარტებიდან გამომდინარეობს მისი გამოთვლის შემდეგი სქემა.

მოდით არგუმენტს მივცეთ ნამატი (დელტა) და ვიპოვოთ ფუნქციის ზრდა:

ვიპოვოთ ფუნქციის გაზრდის შეფარდება არგუმენტის ზრდასთან:

მოდით გამოვთვალოთ ამ თანაფარდობის ლიმიტი იმ პირობით, რომ არგუმენტის ზრდა მიისწრაფვის ნულისკენ, ანუ წარმოებული, რომელიც საჭიროა პრობლემის დებულებაში:

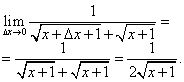
წარმოებულის ფიზიკური მნიშვნელობა

TO წარმოებულის ცნება განაპირობა გალილეო გალილეის მიერ სხეულების თავისუფალი ვარდნის კანონის შესწავლა და უფრო ფართო გაგებით - წერტილის არაერთგვაროვანი მართკუთხა მოძრაობის მყისიერი სიჩქარის პრობლემა.

დაე, კენჭი აწიოს და შემდეგ გაათავისუფლოს დანარჩენი. ბილიკი სდროში გავლილი ტ, არის დროის ფუნქცია, ანუ. s = s(ტ). თუ მოცემულია წერტილის მოძრაობის კანონი, მაშინ შეიძლება განისაზღვროს საშუალო სიჩქარე დროის ნებისმიერი პერიოდისთვის. მოდით, დროის მომენტში კენჭი იყოს პოზიციაში ა, და ამ მომენტში - პოზიციაზე ბ. გარკვეული პერიოდის განმავლობაში (დან ტ) წერტილმა გაიარა გზა. მაშასადამე, მოძრაობის საშუალო სიჩქარე დროის ამ მონაკვეთში, რომელსაც ჩვენ აღვნიშნავთ, არის

.

თუმცა, თავისუფლად ჩამოვარდნილი სხეულის მოძრაობა აშკარად არათანაბარია. სიჩქარე ვშემოდგომა მუდმივად იზრდება. საშუალო სიჩქარე კი აღარ არის საკმარისი მარშრუტის სხვადასხვა მონაკვეთზე მოძრაობის სიჩქარის დასახასიათებლად. რაც უფრო მოკლეა დრო, მით უფრო ზუსტია ეს მახასიათებელი. ამრიგად, შემოღებულია შემდეგი კონცეფცია: მართკუთხა მოძრაობის მყისიერი სიჩქარე (ან სიჩქარე დროის მოცემულ მომენტში ტ) ეწოდება საშუალო სიჩქარის ლიმიტს:

(იმ პირობით, რომ ეს ზღვარი არსებობს და სასრულია).

ასე რომ, გამოდის, რომ მყისიერი სიჩქარე არის ფუნქციის ზრდის შეფარდების ზღვარი. ს(ტ) არგუმენტის მატებამდე ტ at ეს არის წარმოებული, რომელიც ზოგადი ფორმით იწერება შემდეგნაირად:.

.

მითითებული პრობლემის გადაწყვეტა არის წარმოებულის ფიზიკური მნიშვნელობა . ასე რომ, ფუნქციის წარმოებული y=f(x) წერტილში xეწოდება ფუნქციის გაზრდის ზღვარი (თუ ის არსებობს და სასრულია) არგუმენტის ზრდამდე, იმ პირობით, რომ ეს უკანასკნელი ნულისკენ მიისწრაფვის.

მაგალითი 2.იპოვნეთ ფუნქციის წარმოებული

გამოსავალი. წარმოებულის განმარტებიდან გამომდინარეობს მისი გაანგარიშების შემდეგი სქემა.

ნაბიჯი 1. მოდით გავზარდოთ არგუმენტი და ვიპოვოთ

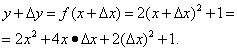
ნაბიჯი 2. იპოვეთ ფუნქციის ზრდა:

ნაბიჯი 3. იპოვეთ ფუნქციის გაზრდის თანაფარდობა არგუმენტის ზრდასთან:

ნაბიჯი 4. გამოთვალეთ ამ თანაფარდობის ლიმიტი ზე, ანუ წარმოებული:

წარმოებულის გეომეტრიული მნიშვნელობა

დაე, ფუნქცია განისაზღვროს ინტერვალზე და მივცეთ წერტილი მფუნქციის გრაფიკზე შეესაბამება არგუმენტის მნიშვნელობას და წერტილს რ- მნიშვნელობა. მოდით გავამახვილოთ ქულები მდა რსწორი ხაზი და დაუძახეთ სეკანტი. მოდი ავღნიშნოთ სეკანტსა და ღერძს შორის კუთხით. ცხადია, ეს კუთხე დამოკიდებულია.

თუ არსებობს

წერტილის გავლას სეკანტის შემზღუდავი პოზიცია ეწოდება ᲑᲐᲢᲝᲜᲘზე (ან ზე).

ტანგენსი ფუნქციის გრაფიკზე წერტილში მსეკანტის ზღვრულ პოზიციას უწოდებენ ᲑᲐᲢᲝᲜᲘზე, ან, რომელიც იგივეა ზე.

განმარტებიდან გამომდინარეობს, რომ ტანგენტის არსებობისთვის საკმარისია ლიმიტის არსებობა

,

ხოლო ზღვარი ტოლია ღერძის მიმართ ტანგენსის დახრის კუთხის.

ახლა მოდით მივცეთ ტანგენსის ზუსტი განმარტება.

ტანგენტიფუნქციის გრაფიკზე წერტილში არის სწორი ხაზი, რომელიც გადის წერტილში და აქვს დახრილობა, ე.ი. სწორი ხაზი, რომლის განტოლება

ამ განმარტებიდან გამომდინარეობს, რომ ფუნქციის წარმოებული უდრის ამ ფუნქციის გრაფიკის ტანგენტის დახრილობას აბსცისის წერტილთან x. ეს არის წარმოებულის გეომეტრიული მნიშვნელობა.

ამოცანა B9 იძლევა ფუნქციის ან წარმოებულის გრაფიკს, საიდანაც თქვენ უნდა განსაზღვროთ შემდეგი სიდიდეებიდან ერთ-ერთი:

1. წარმოებულის მნიშვნელობა რაღაც მომენტში x 0,
2. მაქსიმალური ან მინიმალური ქულები (ექსტრემალური ქულები),
3. მზარდი და კლებადი ფუნქციების ინტერვალები (ერთფეროვნების ინტერვალები).

ამ პრობლემაში წარმოდგენილი ფუნქციები და წარმოებულები ყოველთვის უწყვეტია, რაც გადაწყვეტას ბევრად აადვილებს. იმისდა მიუხედავად, რომ დავალება მათემატიკური ანალიზის განყოფილებას განეკუთვნება, ყველაზე სუსტ მოსწავლეებსაც კი შეუძლიათ ამის გაკეთება, რადგან აქ ღრმა თეორიული ცოდნა არ არის საჭირო.

წარმოებულის, ექსტრემალური წერტილებისა და ერთფეროვნების ინტერვალების მნიშვნელობის საპოვნელად არსებობს მარტივი და უნივერსალური ალგორითმები - ყველა მათგანი ქვემოთ იქნება განხილული.

ყურადღებით წაიკითხეთ B9 პრობლემის პირობები, რათა თავიდან აიცილოთ სულელური შეცდომები: ხანდახან წააწყდებით საკმაოდ ვრცელ ტექსტებს, მაგრამ არის რამდენიმე მნიშვნელოვანი პირობა, რომელიც გავლენას ახდენს ამოხსნის მსვლელობაზე.

წარმოებული მნიშვნელობის გაანგარიშება. ორი წერტილის მეთოდი

თუ პრობლემას მოცემულია f(x) ფუნქციის გრაფიკი, რომელიც ტანგენტია ამ გრაფიკზე რაღაც წერტილში x 0, და საჭიროა ამ ეტაპზე წარმოებულის მნიშვნელობის პოვნა, გამოიყენება შემდეგი ალგორითმი:

1. იპოვეთ ორი „ადეკვატური“ წერტილი ტანგენტის გრაფიკზე: მათი კოორდინატები უნდა იყოს მთელი რიცხვი. ავღნიშნოთ ეს წერტილები A (x 1 ; y 1) და B (x 2 ; y 2). ჩაწერეთ კოორდინატები სწორად - ეს არის ამოხსნის მთავარი წერტილი და ნებისმიერი შეცდომა აქ გამოიწვევს არასწორ პასუხს.
2. კოორდინატების ცოდნით ადვილია არგუმენტის Δx = x 2 − x 1 და Δy = y 2 − y 1 ფუნქციის ნამატის გამოთვლა.
3. საბოლოოდ, ჩვენ ვპოულობთ წარმოებულის მნიშვნელობას D = Δy/Δx. სხვა სიტყვებით რომ ვთქვათ, თქვენ უნდა გაყოთ ფუნქციის ზრდა არგუმენტის ზრდაზე - და ეს იქნება პასუხი.

კიდევ ერთხელ აღვნიშნოთ: A და B წერტილები ზუსტად უნდა ვეძებოთ ტანგენსზე და არა f(x) ფუნქციის გრაფიკზე, როგორც ეს ხშირად ხდება. ტანგენტის ხაზი აუცილებლად შეიცავს მინიმუმ ორ ასეთ წერტილს - წინააღმდეგ შემთხვევაში პრობლემა არ იქნება სწორად ჩამოყალიბებული.

განვიხილოთ წერტილები A (−3; 2) და B (−1; 6) და იპოვეთ ნამატები:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

ვიპოვოთ წარმოებულის მნიშვნელობა: D = Δy/Δx = 4/2 = 2.

დავალება. ნახატზე ნაჩვენებია y = f(x) ფუნქციის გრაფიკი და მასზე ტანგენსი x 0 აბსცისის წერტილში. იპოვეთ f(x) ფუნქციის წარმოებულის მნიშვნელობა x 0 წერტილში.

განვიხილოთ წერტილები A (0; 3) და B (3; 0), იპოვეთ ნამატები:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

ახლა ვპოულობთ წარმოებულის მნიშვნელობას: D = Δy/Δx = −3/3 = −1.

დავალება. ნახატზე ნაჩვენებია y = f(x) ფუნქციის გრაფიკი და მასზე ტანგენსი x 0 აბსცისის წერტილში. იპოვეთ f(x) ფუნქციის წარმოებულის მნიშვნელობა x 0 წერტილში.

განვიხილოთ წერტილები A (0; 2) და B (5; 2) და იპოვეთ ნამატები:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

რჩება წარმოებულის მნიშვნელობის პოვნა: D = Δy/Δx = 0/5 = 0.

ბოლო მაგალითიდან შეგვიძლია ჩამოვაყალიბოთ წესი: თუ ტანგენსი პარალელურია OX ღერძისა, ფუნქციის წარმოებული ტანგენციის წერტილში არის ნული. ამ შემთხვევაში, თქვენ არც კი გჭირდებათ არაფრის დათვლა - უბრალოდ შეხედეთ გრაფიკს.

მაქსიმალური და მინიმალური ქულების გაანგარიშება

ზოგჯერ, ფუნქციის გრაფიკის ნაცვლად, ამოცანა B9 იძლევა წარმოებულის გრაფიკს და მოითხოვს ფუნქციის მაქსიმალური ან მინიმალური წერტილის პოვნას. ამ სიტუაციაში ორპუნქტიანი მეთოდი გამოუსადეგარია, მაგრამ არსებობს სხვა, კიდევ უფრო მარტივი ალგორითმი. პირველ რიგში, მოდით განვსაზღვროთ ტერმინოლოგია:

1. x 0 წერტილს ეწოდება f(x) ფუნქციის მაქსიმალური წერტილი, თუ ამ წერტილის რომელიმე სამეზობლოში მოქმედებს შემდეგი უტოლობა: f(x 0) ≥ f(x).
2. x 0 წერტილს უწოდებენ f(x) ფუნქციის მინიმალურ წერტილს, თუ ამ წერტილის რომელიმე სამეზობლოში მოქმედებს შემდეგი უტოლობა: f(x 0) ≤ f(x).

იმისათვის, რომ იპოვოთ მაქსიმალური და მინიმალური ქულები წარმოებული გრაფიკიდან, უბრალოდ მიჰყევით ამ ნაბიჯებს:

1. გადახაზეთ წარმოებული გრაფიკი, წაშალეთ ყველა არასაჭირო ინფორმაცია. როგორც პრაქტიკა გვიჩვენებს, არასაჭირო მონაცემები მხოლოდ გადაწყვეტილებას ერევა. აქედან გამომდინარე, ჩვენ აღვნიშნავთ წარმოებულის ნულებს კოორდინატთა ღერძზე - და ეს არის ის.
2. გაარკვიეთ წარმოებულის ნიშნები ნულებს შორის ინტერვალებზე. თუ x 0 წერტილისთვის ცნობილია, რომ f'(x 0) ≠ 0, მაშინ შესაძლებელია მხოლოდ ორი ვარიანტი: f'(x 0) ≥ 0 ან f'(x 0) ≤ 0. წარმოებულის ნიშანია მარტივია ორიგინალური ნახაზის დადგენა: თუ წარმოებული გრაფიკი დევს OX ღერძის ზემოთ, მაშინ f'(x) ≥ 0. და პირიქით, თუ წარმოებული გრაფიკი მდებარეობს OX ღერძის ქვემოთ, მაშინ f'(x) ≤ 0.
3. ჩვენ კვლავ ვამოწმებთ წარმოებულის ნულებს და ნიშნებს. სადაც ნიშანი იცვლება მინუსიდან პლუსზე არის მინიმალური წერტილი. პირიქით, თუ წარმოებულის ნიშანი იცვლება პლუსიდან მინუსზე, ეს არის მაქსიმალური წერტილი. დათვლა ყოველთვის კეთდება მარცხნიდან მარჯვნივ.

ეს სქემა მუშაობს მხოლოდ უწყვეტი ფუნქციებისთვის - პრობლემა B9-ში სხვა არ არის.

დავალება. ნახატზე ნაჩვენებია [−5] ინტერვალზე განსაზღვრული f(x) ფუნქციის წარმოებულის გრაფიკი; 5]. იპოვეთ f(x) ფუნქციის მინიმალური წერტილი ამ სეგმენტზე.

მოვიშოროთ არასაჭირო ინფორმაცია და დავტოვოთ მხოლოდ საზღვრები [−5; 5] და x = −3 და x = 2,5 წარმოებულის ნულები. ჩვენ ასევე აღვნიშნავთ ნიშნებს:

ცხადია, x = −3 წერტილში წარმოებულის ნიშანი იცვლება მინუსიდან პლუსზე. ეს არის მინიმალური წერტილი.

დავალება. ნახატზე ნაჩვენებია [−3] ინტერვალზე განსაზღვრული f(x) ფუნქციის წარმოებულის გრაფიკი; 7]. იპოვეთ f(x) ფუნქციის მაქსიმალური წერტილი ამ სეგმენტზე.

მოდით გადავახაზოთ გრაფიკი და დავტოვოთ მხოლოდ საზღვრები [−3; 7] და წარმოებულის ნულები x = −1,7 და x = 5. აღვნიშნოთ წარმოებულის ნიშნები მიღებულ გრაფიკზე. Ჩვენ გვაქვს:

ცხადია, x = 5 წერტილში წარმოებულის ნიშანი იცვლება პლუსიდან მინუსამდე - ეს არის მაქსიმალური წერტილი.

დავალება. ნახატზე ნაჩვენებია f(x) ფუნქციის წარმოებულის გრაფიკი, რომელიც განსაზღვრულია [−6; 4]. იპოვეთ f(x) ფუნქციის მაქსიმალური წერტილების რაოდენობა, რომელიც მიეკუთვნება სეგმენტს [−4; 3].

ამოცანის პირობებიდან გამომდინარეობს, რომ საკმარისია გრაფის მხოლოდ სეგმენტით შეზღუდული ნაწილის გათვალისწინება [−4; 3]. ამიტომ, ვაშენებთ ახალ გრაფიკს, რომელზედაც აღვნიშნავთ მხოლოდ საზღვრებს [−4; 3] და მის შიგნით წარმოებულის ნულები. კერძოდ, წერტილები x = −3.5 და x = 2. მივიღებთ:

ამ გრაფიკზე არის მხოლოდ ერთი მაქსიმალური წერტილი x = 2. სწორედ ამ დროს იცვლება წარმოებულის ნიშანი პლუსიდან მინუსზე.

მცირე შენიშვნა არა მთელი რიცხვის კოორდინატებით წერტილების შესახებ. მაგალითად, ბოლო ამოცანაში განიხილებოდა წერტილი x = −3,5, მაგრამ იგივე წარმატებით შეგვიძლია ავიღოთ x = −3,4. თუ პრობლემა სწორად არის შედგენილი, ასეთი ცვლილებები არ უნდა იმოქმედოს პასუხზე, რადგან პუნქტები „ფიქსირებული საცხოვრებელი ადგილის გარეშე“ უშუალოდ არ მონაწილეობენ პრობლემის გადაჭრაში. რა თქმა უნდა, ეს ხრიკი არ იმუშავებს მთელი რიცხვით.

გაზრდის და კლების ფუნქციების ინტერვალების მოძიება

ასეთ პრობლემაში, როგორც მაქსიმალური და მინიმალური ქულები, შემოთავაზებულია გამოვიყენოთ წარმოებული გრაფიკი იმ უბნების მოსაძებნად, რომლებშიც თავად ფუნქცია იზრდება ან მცირდება. ჯერ განვსაზღვროთ რა არის მატება და კლება:

1. f(x) ფუნქცია იზრდება სეგმენტზე, თუ რომელიმე ორი წერტილისთვის x 1 და x 2 ამ სეგმენტიდან არის შემდეგი განცხადება: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . სხვა სიტყვებით რომ ვთქვათ, რაც უფრო დიდია არგუმენტის მნიშვნელობა, მით უფრო დიდია ფუნქციის მნიშვნელობა.
2. f(x) ფუნქცია მცირდება სეგმენტზე, თუ ამ სეგმენტის ნებისმიერი ორი წერტილისთვის x 1 და x 2 სწორია შემდეგი განცხადება: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . იმათ. უფრო დიდი არგუმენტის მნიშვნელობა შეესაბამება ფუნქციის უფრო მცირე მნიშვნელობას.

მოდით ჩამოვაყალიბოთ საკმარისი პირობები გაზრდისა და შემცირებისთვის:

1. იმისათვის, რომ f(x) უწყვეტი ფუნქცია სეგმენტზე გაიზარდოს, საკმარისია მისი წარმოებული სეგმენტის შიგნით იყოს დადებითი, ე.ი. f'(x) ≥ 0.
2. იმისათვის, რომ f(x) უწყვეტი ფუნქცია სეგმენტზე შემცირდეს, საკმარისია მისი წარმოებული სეგმენტის შიგნით იყოს უარყოფითი, ე.ი. f'(x) ≤ 0.

მოდით მივიღოთ ეს განცხადებები მტკიცებულების გარეშე. ამრიგად, ჩვენ ვიღებთ სქემას ზრდისა და კლების ინტერვალების საპოვნელად, რომელიც მრავალი თვალსაზრისით მსგავსია ექსტრემალური წერტილების გამოთვლის ალგორითმს:

1. წაშალეთ ყველა არასაჭირო ინფორმაცია. წარმოებულის თავდაპირველ გრაფიკში ჩვენ პირველ რიგში გვაინტერესებს ფუნქციის ნულები, ამიტომ მხოლოდ მათ დავტოვებთ.
2. მონიშნეთ წარმოებულის ნიშნები ნულებს შორის ინტერვალებში. სადაც f'(x) ≥ 0, ფუნქცია იზრდება, ხოლო სადაც f'(x) ≤ 0, მცირდება. თუ პრობლემა ადგენს შეზღუდვებს x ცვლადზე, ჩვენ დამატებით აღვნიშნავთ მათ ახალ გრაფიკზე.
3. ახლა, როდესაც ჩვენ ვიცით ფუნქციის ქცევა და შეზღუდვები, რჩება პრობლემაში საჭირო რაოდენობის გამოთვლა.

დავალება. ნახატზე ნაჩვენებია [−3] ინტერვალზე განსაზღვრული f(x) ფუნქციის წარმოებულის გრაფიკი; 7.5]. იპოვეთ f(x) ფუნქციის შემცირების ინტერვალები. თქვენს პასუხში მიუთითეთ ამ ინტერვალებში შემავალი მთელი რიცხვების ჯამი.

ჩვეულებისამებრ, მოდით გადავახაზოთ გრაფიკი და მოვნიშნოთ საზღვრები [−3; 7.5], ასევე x = −1.5 და x = 5.3 წარმოებულის ნულები. შემდეგ ჩვენ აღვნიშნავთ წარმოებულის ნიშნებს. Ჩვენ გვაქვს:

ვინაიდან წარმოებული უარყოფითია ინტერვალზე (− 1.5), ეს არის კლების ფუნქციის ინტერვალი. რჩება ამ ინტერვალის შიგნით არსებული ყველა რიცხვის შეჯამება:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

დავალება. ნახატზე ნაჩვენებია f(x) ფუნქციის წარმოებულის გრაფიკი, რომელიც განსაზღვრულია [−10; 4]. იპოვეთ f(x) ფუნქციის გაზრდის ინტერვალები. თქვენს პასუხში მიუთითეთ მათგან ყველაზე დიდი სიგრძე.

მოვიშოროთ არასაჭირო ინფორმაცია. დავტოვოთ მხოლოდ საზღვრები [−10; 4] და წარმოებულის ნულები, რომელთაგან ამჯერად ოთხი იყო: x = −8, x = −6, x = −3 და x = 2. ავღნიშნოთ წარმოებულის ნიშნები და მივიღოთ შემდეგი სურათი:

ჩვენ გვაინტერესებს ფუნქციის გაზრდის ინტერვალები, ე.ი. ისეთი სადაც f’(x) ≥ 0. გრაფიკზე ორი ასეთი ინტერვალია: (−8; −6) და (−3; 2). გამოვთვალოთ მათი სიგრძე:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

ვინაიდან ჩვენ უნდა ვიპოვოთ ყველაზე დიდი ინტერვალების სიგრძე, პასუხად ვწერთ მნიშვნელობას l 2 = 5.