2009 წლის 19 სექტემბერი
ტესერაქტი (ძველი ბერძნული τέσσερες ἀκτῖνες - ოთხი სხივი) არის ოთხგანზომილებიანი ჰიპერკუბი - კუბის ანალოგი ოთხგანზომილებიან სივრცეში.
გამოსახულება არის ოთხგანზომილებიანი კუბის პროექცია (პერსპექტივა) სამგანზომილებიან სივრცეზე.
ოქსფორდის ლექსიკონის მიხედვით, სიტყვა „ტესერაქტი“ გამოიყენა და გამოიყენა 1888 წელს ჩარლზ ჰოვარდ ჰინტონმა (1853–1907) თავის წიგნში „აზროვნების ახალი ხანა“. მოგვიანებით ზოგიერთმა იმავე ფიგურას „ტეტრაკუბი“ უწოდა.
გეომეტრია
ჩვეულებრივი ტესერაქტი ევკლიდეს ოთხგანზომილებიან სივრცეში განისაზღვრება, როგორც წერტილების ამოზნექილი კორპუსი (±1, ±1, ±1, ±1). სხვა სიტყვებით რომ ვთქვათ, ის შეიძლება წარმოდგენილი იყოს როგორც შემდეგი ნაკრები:
ტესერაქტი შემოიფარგლება რვა ჰიპერპლანით, რომელთა გადაკვეთა თავად ტესერაქტთან განსაზღვრავს მის სამგანზომილებიან სახეებს (რომლებიც ჩვეულებრივი კუბურებია). არაპარალელური 3D სახეების ყოველი წყვილი იკვეთება და ქმნის 2D სახეებს (კვადრატებს) და ა.შ. საბოლოოდ, ტესერაქტს აქვს 8 3D სახე, 24 2D სახე, 32 კიდე და 16 წვერო.
პოპულარული აღწერა
შევეცადოთ წარმოვიდგინოთ როგორი იქნება ჰიპერკუბი სამგანზომილებიანი სივრცის დატოვების გარეშე.
ერთგანზომილებიან „სივრცეში“ - წრფეზე - ვირჩევთ L სიგრძის AB სეგმენტს. AB-დან L მანძილზე მდებარე ორგანზომილებიან სიბრტყეზე ვხატავთ მის პარალელურად DC სეგმენტს და ვაკავშირებთ მათ ბოლოებს. შედეგი არის კვადრატული ABCD. ამ ოპერაციის გამეორებით თვითმფრინავით, ვიღებთ სამგანზომილებიან კუბს ABCDHEFG. ხოლო კუბის მეოთხე განზომილებაში (პირველ სამზე პერპენდიკულარულად) L მანძილით გადაწევით მივიღებთ ჰიპერკუბს ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Construction_tesseract.PNG
ერთგანზომილებიანი სეგმენტი AB ემსახურება ორგანზომილებიანი კვადრატის ABCD მხარეს, კვადრატი - როგორც ABCDHEFG კუბის მხარე, რომელიც, თავის მხრივ, იქნება ოთხგანზომილებიანი ჰიპერკუბის მხარე. სწორი ხაზის სეგმენტს აქვს ორი სასაზღვრო წერტილი, კვადრატს აქვს ოთხი წვერო, ხოლო კუბს აქვს რვა. ოთხგანზომილებიან ჰიპერკუბში იქნება 16 წვერო: საწყისი კუბის 8 წვერო და მეოთხე განზომილებაში გადატანილი 8. მას აქვს 32 კიდე - თითოეული 12 იძლევა ორიგინალური კუბის საწყის და საბოლოო პოზიციებს, ხოლო კიდევ 8 კიდე „ხატავს“ მის რვა წვეროს, რომლებიც გადავიდა მეოთხე განზომილებაში. იგივე მსჯელობა შეიძლება გაკეთდეს ჰიპერკუბის სახეებისთვის. ორგანზომილებიან სივრცეში არის მხოლოდ ერთი (თვით კვადრატი), კუბს აქვს 6 მათგანი (ორი სახე გადატანილი კვადრატიდან და კიდევ ოთხი, რომელიც აღწერს მის გვერდებს). ოთხგანზომილებიან ჰიპერკუბს აქვს 24 კვადრატული სახე - ორიგინალური კუბის 12 კვადრატი ორ პოზიციაზე და 12 კვადრატი მისი თორმეტი კიდედან.
ანალოგიურად, ჩვენ შეგვიძლია გავაგრძელოთ მსჯელობა უფრო დიდი რაოდენობის განზომილებების ჰიპერკუბებზე, მაგრამ გაცილებით საინტერესოა, თუ როგორ მოგვეძებს ოთხგანზომილებიანი ჰიპერკუბი ჩვენ, სამგანზომილებიანი სივრცის მაცხოვრებლებს. ამისთვის გამოვიყენებთ ანალოგიების უკვე ნაცნობ მეთოდს.
ტესერაქტის შეფუთვა
ავიღოთ მავთულის კუბიკი ABCDHEFG და შევხედოთ მას ერთი თვალით კიდის მხრიდან. ჩვენ დავინახავთ და შეგვიძლია დავხატოთ ორი კვადრატი სიბრტყეზე (მისი ახლო და შორეული კიდეები), რომლებიც დაკავშირებულია ოთხი ხაზით - გვერდითი კიდეებით. ანალოგიურად, ოთხგანზომილებიანი ჰიპერკუბი სამგანზომილებიან სივრცეში გამოიყურება როგორც ორი კუბური „ყუთი“, რომლებიც ჩასმულია ერთმანეთში და დაკავშირებულია რვა კიდით. ამ შემთხვევაში, თავად "ყუთები" - სამგანზომილებიანი სახეები - იქნება დაპროექტებული "ჩვენს" სივრცეში და მათი დამაკავშირებელი ხაზები გადაჭიმული იქნება მეოთხე განზომილებაში. თქვენ ასევე შეგიძლიათ სცადოთ წარმოიდგინოთ კუბი არა პროექციაში, არამედ სივრცულ გამოსახულებაში.
ისევე, როგორც სამგანზომილებიანი კუბი იქმნება მისი სახის სიგრძით გადანაცვლებული კვადრატით, მეოთხე განზომილებაში გადატანილი კუბი წარმოქმნის ჰიპერკუბს. იგი შემოიფარგლება რვა კუბიკით, რომლებიც პერსპექტივაში საკმაოდ რთულ ფიგურას წააგავს. ნაწილი, რომელიც დარჩა "ჩვენს" სივრცეში, დახაზულია მყარი ხაზებით, ხოლო ნაწილი, რომელიც შევიდა ჰიპერსივრცეში, დახაზულია წერტილოვანი ხაზებით. ოთხგანზომილებიანი ჰიპერკუბი თავისთავად შედგება უსასრულო რაოდენობის კუბებისგან, ისევე როგორც სამგანზომილებიანი კუბი შეიძლება "დაიჭრას" უსასრულო რაოდენობის ბრტყელ კვადრატებად.
სამგანზომილებიანი კუბის ექვსი სახის მოჭრით, შეგიძლიათ მისი დაშლა ბრტყელ ფიგურად - განვითარებად. მას ექნება კვადრატი ორიგინალური სახის თითოეულ მხარეს, პლუს კიდევ ერთი - მის საპირისპირო სახე. და ოთხგანზომილებიანი ჰიპერკუბის სამგანზომილებიანი განვითარება შედგება ორიგინალური კუბისაგან, მისგან "იზრდება" ექვსი კუბი, პლუს კიდევ ერთი - საბოლოო "ჰიპერფეისი".
ტესერაქტის თვისებები წარმოადგენს ქვედა განზომილების გეომეტრიული ფიგურების თვისებების გაგრძელებას ოთხგანზომილებიან სივრცეში.
პროგნოზები
ორგანზომილებიან სივრცეში
ეს სტრუქტურა ძნელი წარმოსადგენია, მაგრამ შესაძლებელია ტესერაქტის პროექტირება ორგანზომილებიან ან სამგანზომილებიან სივრცეებში. გარდა ამისა, სიბრტყეზე პროექცია აადვილებს ჰიპერკუბის წვეროების ადგილმდებარეობის გაგებას. ამ გზით, შესაძლებელია მივიღოთ სურათები, რომლებიც აღარ ასახავს სივრცით კავშირებს ტეზერაქტის შიგნით, მაგრამ ასახავს წვეროს კავშირის სტრუქტურას, როგორც შემდეგ მაგალითებში:
სამგანზომილებიან სივრცეში
ტესერაქტის პროექცია სამგანზომილებიან სივრცეზე წარმოადგენს ორ ჩადგმულ სამგანზომილებიან კუბს, რომელთა შესაბამისი წვეროები დაკავშირებულია სეგმენტებით. შიდა და გარე კუბებს აქვთ სხვადასხვა ზომის სამგანზომილებიანი სივრცე, მაგრამ ოთხგანზომილებიან სივრცეში ისინი თანაბარი კუბურებია. ყველა ტეზერაქტის კუბის თანასწორობის გასაგებად, შეიქმნა მბრუნავი ტეზერაქტის მოდელი.
ტესერაქტის კიდეების გასწვრივ ექვსი დამსხვრეული პირამიდა ტოლი ექვსი კუბის გამოსახულებაა.
სტერეო წყვილი
ტესერაქტის სტერეო წყვილი გამოსახულია, როგორც ორი პროექცია სამგანზომილებიან სივრცეზე. ტესერაქტის ეს სურათი შექმნილია იმისთვის, რომ წარმოედგინა სიღრმე მეოთხე განზომილებაში. სტერეო წყვილი ისეა დანახული, რომ თითოეული თვალი ხედავს ამ სურათებიდან მხოლოდ ერთს, ჩნდება სტერეოსკოპიული სურათი, რომელიც ასახავს ტესერაქტის სიღრმეს.
ტესერაქტის შეფუთვა
ტესერაქტის ზედაპირი შეიძლება გაიშალოს რვა კუბად (ისევე, როგორც კუბის ზედაპირი შეიძლება გაიშალოს ექვს კვადრატად). არსებობს 261 განსხვავებული ტესერაქტის დიზაინი. ტესერაქტის გაშლა შეიძლება გამოითვალოს დაკავშირებული კუთხეების გრაფიკზე გამოსახვით.
ტესერაქტი ხელოვნებაში
ედვინა ა-ს „ახალ აბბოტის დაბლობში“ ჰიპერკუბი მთხრობელის როლს ასრულებს.
ჯიმი ნეიტრონის თავგადასავლების ერთ ეპიზოდში: "ბიჭის გენიოსი", ჯიმი იგონებს ოთხგანზომილებიან ჰიპერკუბს, რომელიც იდენტურია ჰაინლეინის 1963 წლის რომანიდან "დიდების გზა"-დან.
რობერტ ე. ჰაინლეინმა ახსენა ჰიპერკუბები სულ მცირე სამ სამეცნიერო ფანტასტიკურ მოთხრობაში. ოთხი განზომილების სახლში (The House That Teal Built) (1940) მან აღწერა სახლი, რომელიც აშენებულია შეუფუთავი ტესერაქტივით.
ჰაინლეინის რომანი დიდების გზა აღწერს ჰიპერ ზომის კერძებს, რომლებიც შიგნიდან უფრო დიდი იყო, ვიდრე გარედან.
ჰენრი კუტნერის მოთხრობა "Mimsy Were the Borogoves" აღწერს საგანმანათლებლო სათამაშოს ბავშვებისთვის შორეული მომავლისგან, სტრუქტურით მსგავსი ტესერაქტის.
ალექს გარლანდის რომანში (1999) ტერმინი "ტესერაქტი" გამოიყენება ოთხგანზომილებიანი ჰიპერკუბის სამგანზომილებიანი გაშლისთვის, ვიდრე თავად ჰიპერკუბის. ეს არის მეტაფორა, რომელიც შექმნილია იმის დასანახად, რომ შემეცნებითი სისტემა უნდა იყოს უფრო ფართო, ვიდრე შეცნობადი.
კუბი 2-ის სიუჟეტი: ჰიპერკუბი ორიენტირებულია რვა უცნობზე, რომლებიც ჩარჩენილია "ჰიპერკუბში", ან დაკავშირებული კუბების ქსელში.
სატელევიზიო სერიალი ანდრომედა იყენებს ტესერაქტის გენერატორებს, როგორც სიუჟეტის მოწყობილობას. ისინი ძირითადად შექმნილია სივრცისა და დროის მანიპულირებისთვის.
სალვადორ დალის ნახატი "ჯვარცმა" (კორპუსის ჰიპერკუბუსი) (1954)
Nextwave-ის კომიქსები ასახავს მანქანას, რომელიც მოიცავს 5 ტეზერაქტის ზონას.
ალბომში Voivod Nothingface ერთ-ერთ კომპოზიციას ჰქვია "ჩემს ჰიპერკუბში".
ენტონი პირსის რომანში Route Cube, საერთაშორისო განვითარების ასოციაციის ერთ-ერთ ორბიტაზე მომუშავე მთვარე ეწოდება ტესერაქტს, რომელიც შეკუმშულია 3 განზომილებაში.
სერიალში "შავი ხვრელის სკოლა" მესამე სეზონში არის ეპიზოდი "ტესერაქტი". ლუკასი აჭერს საიდუმლო ღილაკს და სკოლა იწყებს ფორმას, როგორც მათემატიკური ტესერაქტი.
ტერმინი „ტესერაქტი“ და მისი წარმოებული ტერმინი „ტესერატი“ გვხვდება მადლენ ლ'ენგლის მოთხრობაში „დროის ნაოჭი“.
ჰიპერკუბური და პლატონური მყარი
შეკვეცილი იკოსაედრონის ("ფეხბურთის ბურთი") მოდელირება "ვექტორი" სისტემაში
რომელშიც თითოეული ხუთკუთხედი შემოსაზღვრულია ექვსკუთხედებით
შეკვეცილი იკოსაედონიშეიძლება მიღებულ იქნეს 12 წვეროს მოწყვეტით, რათა ჩამოყალიბდეს სახეები ჩვეულებრივი ხუთკუთხედების სახით. ამ შემთხვევაში ახალი მრავალწახნაგების წვეროების რაოდენობა იზრდება 5-ჯერ (12×5=60), 20 სამკუთხა სახე იქცევა რეგულარულ ექვსკუთხედებად (სულ სახეები ხდება 20+12=32), ა კიდეების რაოდენობა იზრდება 30+12×5=90-მდე.







ვექტორულ სისტემაში შეკვეცილი იკოსაედრონის აგების ნაბიჯები
ფიგურები 4 განზომილებიან სივრცეში.
 --à
--à

 --à
?
--à
?
მაგალითად, მოცემულია კუბი და ჰიპერკუბი. ჰიპერკუბს აქვს 24 სახე. ეს ნიშნავს, რომ 4 განზომილებიანი ოქტაედრონს ექნება 24 წვერო. თუმცა არა, ჰიპერკუბს აქვს კუბის 8 სახე - თითოეულს აქვს ცენტრი თავის წვეროზე. ეს ნიშნავს, რომ 4 განზომილებიან რვაგანზომილებიანს ექნება 8 წვერო, რაც კიდევ უფრო მსუბუქია.


4 განზომილებიანი ოქტაედონი. იგი შედგება რვა ტოლგვერდა და თანაბარი ტეტრაედრებისაგან,
თითოეულ წვეროზე ოთხით არის დაკავშირებული.






ბრინჯი. სიმულაციის მცდელობა
ჰიპერსფერო-ჰიპერსფერო ვექტორულ სისტემაში
წინა - უკანა სახეები - ბურთები დამახინჯების გარეშე. კიდევ ექვსი ბურთი შეიძლება განისაზღვროს ელიფსოიდების ან კვადრატული ზედაპირის მეშვეობით (4 კონტურის ხაზის მეშვეობით, როგორც გენერატორები) ან სახეების მეშვეობით (პირველად განსაზღვრულია გენერატორების მეშვეობით).


მეტი ტექნიკა ჰიპერსფეროს "აშენებისთვის".
- იგივე "ფეხბურთის ბურთი" 4 განზომილებიან სივრცეში
დანართი 2
ამოზნექილი პოლიედრებისთვის არის თვისება, რომელიც აკავშირებს მისი წვეროების, კიდეების და სახეების რაოდენობას, რომელიც დაამტკიცა 1752 წელს ლეონჰარდ ეილერმა და უწოდა ეილერის თეორემა.
მის ჩამოყალიბებამდე განვიხილოთ ჩვენთვის ცნობილი პოლიედრები და შეავსეთ შემდეგი ცხრილი, რომელშიც B არის მოცემული პოლიედრონის წვეროების რაოდენობა, P - კიდეები და G - სახეები:
|
პოლიედრონის სახელი |
|||
|
სამკუთხა პირამიდა |
|||
|
ოთხკუთხა პირამიდა |
|||
|
Სამკუთხა პრიზმა |
|||
|
ოთხკუთხა პრიზმა |
|||
|
n-ქვანახშირის პირამიდა |
ნ+1 |
2ნ |
ნ+1 |
|
n-ნახშირბადის პრიზმა |
2ნ |
3ნ |
n+2 |
|
n-ნახშირი შეკვეცილი პირამიდა |
2ნ |
3ნ |
n+2 |
ამ ცხრილიდან მაშინვე ირკვევა, რომ ყველა შერჩეული პოლიედრისთვის მოქმედებს ტოლობა B - P + G = 2. გამოდის, რომ ეს ტოლობა მოქმედებს არა მხოლოდ ამ პოლიედრებისთვის, არამედ თვითნებური ამოზნექილი პოლიედრებისთვისაც.
ეილერის თეორემა. ნებისმიერი ამოზნექილი პოლიედრონისთვის თანასწორობა მოქმედებს
B - P + G = 2,
სადაც B არის წვეროების რაოდენობა, P არის კიდეების რაოდენობა და G არის მოცემული პოლიედრონის სახეების რაოდენობა.
მტკიცებულება.ამ თანასწორობის დასამტკიცებლად, წარმოიდგინეთ ელასტიური მასალისგან დამზადებული ამ პოლიედრონის ზედაპირი. მოვაცილოთ (ამოვჭრათ) მისი ერთი სახე და დარჩენილი ზედაპირი გავჭიმოთ სიბრტყეზე. ჩვენ ვიღებთ მრავალკუთხედს (რომელიც წარმოიქმნება მრავალკუთხედის ამოღებული სახის კიდეებით), დაყოფილია უფრო პატარა მრავალკუთხედებად (წარმოქმნილია მრავალწახნაგების დარჩენილი სახეებით).
გაითვალისწინეთ, რომ მრავალკუთხედები შეიძლება იყოს დეფორმირებული, გადიდებული, შემცირებული ან თუნდაც მრუდე მათი გვერდები, თუ გვერდებზე ხარვეზები არ არის. წვეროების, კიდეების და სახეების რაოდენობა არ შეიცვლება.
დავამტკიცოთ, რომ პოლიგონის დაყოფა უფრო მცირე მრავალკუთხედებად აკმაყოფილებს თანასწორობას
(*)B - P + G" = 1,
სადაც B არის წვეროების მთლიანი რაოდენობა, P არის კიდეების საერთო რაოდენობა და Г " არის დანაყოფის შემადგენლობაში შემავალი მრავალკუთხედების რაოდენობა. ცხადია, რომ Г " = Г - 1, სადაც Г არის მოცემულის სახეების რაოდენობა. მრავალწახნაგოვანი.
დავამტკიცოთ, რომ ტოლობა (*) არ იცვლება, თუ დიაგონალი დახაზულია მოცემული დანაყოფის ზოგიერთ მრავალკუთხედში (სურ. 5, ა). მართლაც, ასეთი დიაგონალის დახაზვის შემდეგ ახალ დანაყოფს ექნება B წვეროები, P+1 კიდეები და მრავალკუთხედების რაოდენობა გაიზრდება ერთით. ამიტომ გვაქვს
B - (P + 1) + (G "+1) = B - P + G " .

ამ თვისების გამოყენებით ვხატავთ დიაგონალებს, რომლებიც ყოფენ შემომავალ მრავალკუთხედებს სამკუთხედებად და მიღებული დანაყოფისთვის ვაჩვენებთ ტოლობის მიზანშეწონილობას (*) (ნახ. 5, ბ). ამისათვის ჩვენ თანმიმდევრულად ამოვიღებთ გარე კიდეებს, ვამცირებთ სამკუთხედების რაოდენობას. ამ შემთხვევაში შესაძლებელია ორი შემთხვევა:
ა) სამკუთხედის ამოღება ABCაუცილებელია ორი ნეკნის ამოღება, ჩვენს შემთხვევაში ABდა ძვ.წ.;
ბ) სამკუთხედის ამოღებაMKNაუცილებელია ერთი კიდის ამოღება, ჩვენს შემთხვევაშიMN.
ორივე შემთხვევაში თანასწორობა (*) არ შეიცვლება. მაგალითად, პირველ შემთხვევაში, სამკუთხედის ამოღების შემდეგ, გრაფიკი შედგება B - 1 წვერო, P - 2 კიდეები და G " - 1 მრავალკუთხედი:
(B - 1) - (P + 2) + (G " – 1) = B – P + G ".
მეორე შემთხვევა თავად განიხილეთ.
ამრიგად, ერთი სამკუთხედის ამოღება არ ცვლის ტოლობას (*). სამკუთხედების ამოღების ამ პროცესის გაგრძელებით, ჩვენ საბოლოოდ მივაღწევთ დანაყოფს, რომელიც შედგება ერთი სამკუთხედისგან. ასეთი დანაყოფისთვის B = 3, P = 3, Г " = 1 და, მაშასადამე, B – Р + Г " = 1. ეს ნიშნავს, რომ ტოლობა (*) ასევე მოქმედებს თავდაპირველ დანაყოფზე, საიდანაც საბოლოოდ ვიღებთ იმას, რომ რადგან მრავალკუთხედის ტოლობის ეს დანაყოფი (*) მართალია. ამრიგად, თავდაპირველი ამოზნექილი პოლიედრონისთვის ტოლობა B - P + G = 2 მართალია.
პოლიედრონის მაგალითი, რომლისთვისაც ეილერის მიმართება არ მოქმედებს,ნაჩვენებია სურათზე 6. ამ პოლიედრონს აქვს 16 წვერო, 32 კიდე და 16 სახე. ამრიგად, ამ პოლიედრონისთვის მოქმედებს ტოლობა B – P + G = 0.
დანართი 3.
ფილმი კუბი 2: ჰიპერკუბი არის სამეცნიერო ფანტასტიკური ფილმი, ფილმის კუბის გაგრძელება.
რვა უცხო ადამიანი იღვიძებს კუბის ფორმის ოთახებში. ოთახები განლაგებულია ოთხგანზომილებიანი ჰიპერკუბის შიგნით. ოთახები გამუდმებით მოძრაობს „კვანტური ტელეპორტაციის“ საშუალებით და თუ გვერდით ოთახში ახვალთ, ნაკლებად სავარაუდოა, რომ წინა ოთახში დაბრუნდეთ. პარალელური სამყაროები იკვეთება ჰიპერკუბში, დრო განსხვავებულად მიედინება ზოგიერთ ოთახში, ზოგი ოთახი კი სიკვდილის ხაფანგია.
ფილმის სიუჟეტი დიდწილად იმეორებს პირველი ნაწილის ისტორიას, რაც ასევე აისახება ზოგიერთი პერსონაჟის გამოსახულებაში. ნობელის პრემიის ლაურეატი როზენცვეიგი, რომელმაც გამოთვალა ჰიპერკუბის განადგურების ზუსტი დრო, კვდება ჰიპერკუბის ოთახებში..
კრიტიკა
თუ პირველ ნაწილში ლაბირინთში ჩაკეტილი ადამიანები ერთმანეთის დახმარებას ცდილობდნენ, ამ ფილმში ყველა ადამიანი თავისთვისაა. არსებობს უამრავი არასაჭირო სპეციალური ეფექტი (აკა ხაფანგები), რომლებიც არავითარ შემთხვევაში ლოგიკურად არ აკავშირებენ ფილმის ამ ნაწილს წინასთან. ანუ გამოდის, რომ ფილმი კუბი 2 არის მომავლის 2020-2030 წლების ერთგვარი ლაბირინთი, მაგრამ არა 2000. პირველ ნაწილში ყველა სახის ხაფანგი თეორიულად შეიძლება ადამიანმა შექმნას. მეორე ნაწილში ეს ხაფანგები არის ერთგვარი კომპიუტერული პროგრამა, ე.წ. „ვირტუალური რეალობა“.
გეომეტრიაში ჰიპერკუბი- ეს ნ- კვადრატის განზომილებიანი ანალოგია ( ნ= 2) და კუბი ( ნ= 3). ეს არის დახურული ამოზნექილი ფიგურა, რომელიც შედგება პარალელური ხაზების ჯგუფებისგან, რომლებიც განლაგებულია ფიგურის მოპირდაპირე კიდეებზე და ერთმანეთთან დაკავშირებულია სწორი კუთხით.
ეს მაჩვენებელი ასევე ცნობილია როგორც ტესერაქტი(ტესერაქტი). ტესერაქტი არის კუბის მიმართ, როგორც კუბი კვადრატში. უფრო ფორმალურად, ტესერაქტი შეიძლება შეფასდეს, როგორც რეგულარული ამოზნექილი ოთხგანზომილებიანი პოლიტოპი (პოლიედრონი), რომლის საზღვარი შედგება რვა კუბური უჯრედისგან.
ოქსფორდის ინგლისური ლექსიკონის მიხედვით, სიტყვა „ტესერაქტი“ 1888 წელს ჩარლზ ჰოვარდ ჰინტონმა გამოიყენა და გამოიყენა წიგნში „აზროვნების ახალი ერა“. სიტყვა მომდინარეობს ბერძნულიდან "τεσσερες ακτινες" ("ოთხი სხივი"), ოთხი კოორდინატული ღერძის სახით. გარდა ამისა, ზოგიერთ წყაროში იგივე ფიგურა ეწოდებოდა ტეტრაკუბი(ტეტრაკუბი).
ნ-განზომილებიან ჰიპერკუბსაც უწოდებენ n-კუბი.
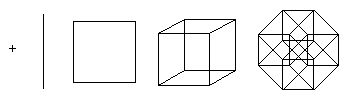
წერტილი არის 0 განზომილების ჰიპერკუბი. თუ წერტილი გადაიტანეთ სიგრძის ერთეულით, მიიღებთ ერთეული სიგრძის სეგმენტს - 1 განზომილების ჰიპერკუბს. გარდა ამისა, თუ სეგმენტს გადაიტანეთ სიგრძის ერთეულით პერპენდიკულარული მიმართულებით. სეგმენტის მიმართულებამდე მიიღებთ კუბს - მე-2 განზომილების ჰიპერკუბს. კვადრატის სიგრძის ერთეულით გადაადგილებით კვადრატის სიბრტყეზე პერპენდიკულარული მიმართულებით, მიიღება კუბი - მე-3 განზომილების ჰიპერკუბი. ეს პროცესი შეიძლება განზოგადდეს ნებისმიერი რაოდენობის განზომილებაზე. მაგალითად, თუ მეოთხე განზომილებაში გადაიტანეთ კუბი სიგრძის ერთი ერთეულით, მიიღებთ ტესერაქტს.
ჰიპერკუბების ოჯახი ერთ-ერთია იმ რამდენიმე რეგულარული პოლიედრიდან, რომელიც შეიძლება წარმოდგენილი იყოს ნებისმიერ განზომილებაში.
ჰიპერკუბის ელემენტები
განზომილების ჰიპერკუბი ნაქვს 2 ნ„გვერდები“ (ერთგანზომილებიან ხაზს აქვს 2 წერტილი; ორგანზომილებიან კვადრატს აქვს 4 გვერდი; სამგანზომილებიან კუბს აქვს 6 სახე; ოთხგანზომილებიან ტესერაქტს აქვს 8 უჯრედი). ჰიპერკუბის წვეროების (წერტილების) რაოდენობა არის 2 ნ(მაგალითად, კუბისთვის - 2 3 წვერო).
რაოდენობა მ- განზომილებიანი ჰიპერკუბები საზღვარზე ნ-კუბი უდრის
მაგალითად, ჰიპერკუბის საზღვარზე არის 8 კუბი, 24 კვადრატი, 32 კიდე და 16 წვერო.
| n-კუბი | სახელი | ვერტექსი (0-სახე) |
ზღვარი (1-სახე) |
ზღვარი (2-სახე) |
უჯრედი (3-სახე) |
(4-სახე) | (5-სახე) | (6 გვერდითი) | (7-სახე) | (8-სახე) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-კუბი | Წერტილი | 1 | ||||||||
| 1-კუბი | ხაზის სეგმენტი | 2 | 1 | |||||||
| 2-კუბი | მოედანი | 4 | 4 | 1 | ||||||
| 3-კუბი | კუბი | 8 | 12 | 6 | 1 | |||||
| 4-კუბი | ტესერაქტი | 16 | 32 | 24 | 8 | 1 | ||||
| 5-კუბი | პენტერაქტი | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-კუბი | ჰექსერაქტი | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-კუბი | ჰეპტერაქტი | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-კუბი | ოქტერაქტი | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-კუბი | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
პროექცია თვითმფრინავზე
ჰიპერკუბის წარმოქმნა შეიძლება წარმოდგენილი იყოს შემდეგნაირად:
- ორი წერტილი A და B შეიძლება დაუკავშირდეს ხაზის სეგმენტს AB.
- ორი პარალელური სეგმენტი AB და CD შეიძლება იყოს დაკავშირებული კვადრატული ABCD-ის შესაქმნელად.
- ორი პარალელური კვადრატი ABCD და EFGH შეიძლება დაუკავშირდეს ABCDEFGH კუბის შესაქმნელად.
- ორი პარალელური კუბი ABCDEFGH და IJKLMNOP შეიძლება იყოს დაკავშირებული ჰიპერკუბის ABCDEFGHIJKLMNOP-ის შესაქმნელად.
ამ უკანასკნელის სტრუქტურის ვიზუალიზაცია ადვილი არ არის, მაგრამ შესაძლებელია მისი პროექციის გამოსახვა ორგანზომილებიან ან სამგანზომილებიან სივრცეში. უფრო მეტიც, პროგნოზები ორგანზომილებიან სიბრტყეზე შეიძლება იყოს უფრო სასარგებლო, თუ დაუშვით დაპროექტებული წვეროების პოზიციების გადაკეთება. ამ შემთხვევაში შესაძლებელია გამოსახულებების მიღება, რომლებიც აღარ ასახავს ელემენტების სივრცულ კავშირებს ტესერაქტის შიგნით, მაგრამ ასახავს წვეროების კავშირების სტრუქტურას, როგორც ქვემოთ მოცემულ მაგალითებში.

პირველი ილუსტრაცია გვიჩვენებს, თუ როგორ წარმოიქმნება ტესერაქტი ორი კუბის შეერთებით. ეს სქემა ორი კვადრატიდან კუბის შექმნის სქემის მსგავსია. მეორე დიაგრამა გვიჩვენებს, რომ ტესერაქტის ყველა კიდე ერთი და იგივე სიგრძეა. ეს სქემა ასევე გაიძულებთ მოძებნოთ ერთმანეთთან დაკავშირებული კუბურები. მესამე დიაგრამაში, ტესერაქტის წვეროები განლაგებულია ზედა წერტილთან მიმართებაში არსებული მანძილების შესაბამისად. ეს სქემა საინტერესოა, რადგან იგი გამოიყენება როგორც ძირითადი სქემა პროცესორების დამაკავშირებელი ქსელის ტოპოლოგიისთვის, პარალელური გამოთვლის ორგანიზებისას: მანძილი ნებისმიერ ორ კვანძს შორის არ აღემატება 4 კიდეების სიგრძეს და არსებობს მრავალი განსხვავებული გზა დატვირთვის დასაბალანსებლად.
ჰიპერკუბი ხელოვნებაში
ჰიპერკუბი სამეცნიერო ფანტასტიკურ ლიტერატურაში 1940 წლიდან გამოჩნდა, როდესაც რობერტ ჰაინლეინმა მოთხრობაში "და მან ააგო მრუდე სახლი" აღწერა ტესერაქტის სკანირების სახით აშენებული სახლი. სიუჟეტში, ეს შემდეგი, ეს სახლი ინგრევა, გადაიქცევა ოთხგანზომილებიან ტესერაქტად. ამის შემდეგ, ჰიპერკუბი ჩნდება ბევრ წიგნსა და მოთხრობაში.
ფილმი Cube 2: Hypercube არის დაახლოებით რვა ადამიანი, რომლებიც ხაფანგში არიან ჰიპერკუბების ქსელში.
სალვადორ დალის ნახატზე "ჯვარცმა (Corpus Hypercubus)", 1954 წ. ეს ნახატი შეგიძლიათ ნახოთ ნიუ იორკის მეტროპოლიტენის ხელოვნების მუზეუმში.
დასკვნა
ჰიპერკუბი ერთ-ერთი უმარტივესი ოთხგანზომილებიანი ობიექტია, საიდანაც ჩანს მეოთხე განზომილების სირთულე და უჩვეულოობა. და ის, რაც შეუძლებლად გამოიყურება სამ განზომილებაში, შესაძლებელია ოთხში, მაგალითად, შეუძლებელ ფიგურაში. ასე, მაგალითად, შეუძლებელი სამკუთხედის ზოლები ოთხ განზომილებაში იქნება დაკავშირებული სწორი კუთხით. და ეს ფიგურა ასე გამოიყურება ყველა ხედვის წერტილიდან და არ იქნება დამახინჯებული, სამგანზომილებიან სივრცეში შეუძლებელი სამკუთხედის განხორციელებისგან განსხვავებით (იხ.
მრავალგანზომილებიანი სივრცეების დოქტრინა მე-19 საუკუნის შუა ხანებიდან გამოჩნდა გ.გრასმანის, ა.კეილის, ბ.რიმანის, ვ.კლიფორდის, ლ.შლაფლის და სხვა მათემატიკოსების ნაშრომებში. მე-20 საუკუნის დასაწყისში, ა.აინშტაინის ფარდობითობის თეორიისა და გ.მინკოვსკის იდეების მოსვლასთან ერთად, ფიზიკაში დაიწყო ოთხგანზომილებიანი სივრცე-დროის კოორდინატთა სისტემის გამოყენება.
შემდეგ ოთხგანზომილებიანი სივრცის იდეა მეცნიერებისგან ისესხეს სამეცნიერო ფანტასტიკის მწერლებმა. თავიანთ ნამუშევრებში მათ მსოფლიოს უამბეს მეოთხე განზომილების საოცარი საოცრებების შესახებ. მათი ნამუშევრების გმირებს, ოთხგანზომილებიანი სივრცის თვისებების გამოყენებით, შეეძლოთ კვერცხის შიგთავსის ჭამა ნაჭუჭის დაზიანების გარეშე და სასმელის დალევა ბოთლის თავსახურის გახსნის გარეშე. ქურდებმა საგანძური სეიფიდან მეოთხე განზომილებაში ამოიღეს. ჯაჭვის რგოლები ადვილად იშლება და თოკზე არსებული კვანძი მისი ბოლოების შეხების გარეშე შეიძლება. ქირურგები ატარებდნენ ოპერაციებს შინაგან ორგანოებზე პაციენტის სხეულის ქსოვილის მოჭრის გარეშე. მისტიკოსებმა მიცვალებულთა სულები მეოთხე განზომილებაში მოათავსეს. უბრალო ადამიანისთვის ოთხგანზომილებიანი სივრცის იდეა გაუგებარი და იდუმალი დარჩა და ბევრი ზოგადად ოთხგანზომილებიან სივრცეს მეცნიერებისა და სამეცნიერო ფანტასტიკის მწერლების ფანტაზიის ნაყოფი თვლის, რომელსაც არაფერი აქვს საერთო რეალობასთან.
აღქმის პრობლემა
ტრადიციულად ითვლება, რომ ადამიანს არ შეუძლია ოთხგანზომილებიანი ფიგურების აღქმა და წარმოდგენა, რადგან ის სამგანზომილებიანი არსებაა. სუბიექტი აღიქვამს სამგანზომილებიან ფიგურებს ბადურის გამოყენებით, რომელიც ორგანზომილებიანია. ოთხგანზომილებიანი ფიგურების აღქმისთვის საჭიროა სამგანზომილებიანი ბადურა, მაგრამ ადამიანებს ეს უნარი არ გააჩნიათ.
ოთხგანზომილებიანი ფიგურების მკაფიო წარმოდგენა რომ მივიღოთ, ჩვენ გამოვიყენებთ ანალოგებს ქვედა განზომილებიანი სივრცეებიდან უფრო მაღალგანზომილებიან ფიგურებზე ექსტრაპოლაციისთვის, მოდელირების მეთოდს და გამოვიყენებთ სისტემების ანალიზის მეთოდებს ოთხგანზომილებიანი ელემენტებს შორის შაბლონების მოსაძებნად. განზომილებიანი ფიგურები. შემოთავაზებულმა მოდელებმა ადეკვატურად უნდა აღწერონ ოთხგანზომილებიანი ფიგურების თვისებები, არ ეწინააღმდეგებოდეს ერთმანეთს და მისცეს საკმარისი გაგება ოთხგანზომილებიანი ფიგურისა და, პირველ რიგში, მისი გეომეტრიული ფორმის შესახებ. ვინაიდან ლიტერატურაში არ არსებობს ოთხგანზომილებიანი ფიგურების სისტემატური და ვიზუალური აღწერა, არამედ მხოლოდ მათი სახელები მიუთითებს ზოგიერთ თვისებაზე, ჩვენ ვთავაზობთ ოთხგანზომილებიანი ფიგურების შესწავლას დავიწყოთ უმარტივესი - ოთხგანზომილებიანი კუბით, რომელიც ე.წ. ჰიპერკუბი.
ჰიპერკუბის განმარტება
ჰიპერკუბიარის ჩვეულებრივი პოლიტოპი, რომლის უჯრედი არის კუბი.
პოლიტოპიარის ოთხგანზომილებიანი ფიგურა, რომლის საზღვარი შედგება პოლიედრებისაგან. პოლიტოპური უჯრედის ანალოგი არის პოლიედრონის სახე. ჰიპერკუბი არის სამგანზომილებიანი კუბის ანალოგი.
ჩვენ გვექნება წარმოდგენა ჰიპერკუბის შესახებ, თუ ვიცით მისი თვისებები. სუბიექტი აღიქვამს გარკვეულ ობიექტს, წარმოადგენს მას გარკვეული მოდელის სახით. მოდით გამოვიყენოთ ეს მეთოდი და წარმოვადგინოთ ჰიპერკუბის იდეა სხვადასხვა მოდელების სახით.
ანალიტიკური მოდელი
ჩვენ განვიხილავთ ერთგანზომილებიან სივრცეს (სწორი ხაზი), როგორც წერტილების მოწესრიგებული ნაკრებიმ(x), სად x– წრფის თვითნებური წერტილის კოორდინატი. შემდეგ ერთეულის სეგმენტი მითითებულია ორი წერტილის მითითებით:ა(0) და ბ(1).
სიბრტყე (ორგანზომილებიანი სივრცე) შეიძლება ჩაითვალოს წერტილების მოწესრიგებულ კომპლექტად მ(x; წ). ერთეულის კვადრატი მთლიანად განისაზღვრება მისი ოთხი წვერით: ა(0; 0), ბ(1; 0), C(1; 1), დ(0; 1). კვადრატის წვეროების კოორდინატები მიიღება სეგმენტის კოორდინატებზე ნულის და შემდეგ ერთის მიმატებით.
სამგანზომილებიანი სივრცე - პუნქტების მოწესრიგებული ნაკრები მ(x; წ; ზ). სამგანზომილებიანი კუბის დასადგენად საჭიროა რვა ქულა:
ა(0; 0; 0), ბ(1; 0; 0), C(1; 1; 0), დ(0; 1; 0),
ე(0; 0; 1), ფ(1; 0; 1), გ(1; 1; 1), ჰ(0; 1; 1).
კუბის კოორდინატები მიიღება კვადრატის კოორდინატებიდან ნულის და შემდეგ ერთის მიმატებით.
ოთხგანზომილებიანი სივრცე არის წერტილების მოწესრიგებული ნაკრები მ(x; წ; ზ; ტ). ჰიპერკუბის დასადგენად, თქვენ უნდა განსაზღვროთ მისი თექვსმეტი წვერის კოორდინატები:
ა(0; 0; 0; 0), ბ(1; 0; 0; 0), C(1; 1; 0; 0), დ(0; 1; 0; 0),
ე(0; 0; 1; 0), ფ(1; 0; 1; 0), გ(1; 1; 1; 0), ჰ(0; 1; 1; 0),
კ(0; 0; 0; 1), ლ(1; 0; 0; 1), მ(1; 1; 0; 1), ნ(0; 1; 0; 1),
ო(0; 0; 1; 1), პ(1; 0; 1; 1), რ(1; 1; 1; 1), ს(0; 1; 1; 1).
ჰიპერკუბის კოორდინატები მიიღება სამგანზომილებიანი კუბის კოორდინატებიდან მეოთხე კოორდინატის ტოლი ნულის და შემდეგ ერთის მიმატებით.
ოთხგანზომილებიანი ევკლიდური სივრცისთვის ანალიტიკური გეომეტრიის ფორმულების გამოყენებით, შეიძლება მივიღოთ ჰიპერკუბის თვისებები.
მაგალითად, განვიხილოთ ჰიპერკუბის მთავარი დიაგონალის სიგრძის გამოთვლა. დავუშვათ, ჩვენ უნდა ვიპოვოთ მანძილი წერტილებს შორის ა(0, 0, 0, 0) და რ(1, 1, 1, 1). ამისათვის ჩვენ გამოვიყენებთ მანძილის ფორმულას ოთხგანზომილებიან ევკლიდეს სივრცეში.
ორგანზომილებიან სივრცეში (სიბრტყეზე), მანძილი წერტილებს შორის ა(x 1 , წ 1) და ბ(x 2 , წ 2) გამოითვლება ფორმულით
ეს ფორმულა გამომდინარეობს პითაგორას თეორემიდან.
წერტილებს შორის მანძილის შესაბამისი ფორმულა ა(x 1 , წ 1 , ზ 1) და ბ(x 2 , წ 2 , ზ 2) სამგანზომილებიან სივრცეში აქვს ფორმა
და ერთგანზომილებიან სივრცეში (სწორ ხაზზე) წერტილებს შორის A( x 1) და B ( x 2) შეგიძლიათ დაწეროთ შესაბამისი მანძილის ფორმულა:
ანალოგიურად, მანძილი წერტილებს შორის ა(x 1 , წ 1 , ზ 1 , ტ 1) და ბ(x 2 , წ 2 , ზ 2 , ტ 2) ოთხგანზომილებიან სივრცეში გამოითვლება ფორმულით:
შემოთავაზებული მაგალითისთვის ვხვდებით
ამრიგად, ჰიპერკუბი არსებობს ანალიტიკურად და მისი თვისებები არ შეიძლება აღიწეროს არა უარესი, ვიდრე სამგანზომილებიანი კუბის თვისებები.
დინამიური მოდელი
ჰიპერკუბის ანალიტიკური მოდელი ძალიან აბსტრაქტულია, ამიტომ განვიხილოთ სხვა მოდელი - დინამიური.
წერტილი (ნულ განზომილებიანი ფიგურა), რომელიც მოძრაობს ერთი მიმართულებით, წარმოქმნის სეგმენტს (ერთგანზომილებიან ფიგურას). სეგმენტი, რომელიც მოძრაობს თავის მიმართ პერპენდიკულარული მიმართულებით, ქმნის კვადრატს (ორგანზომილებიან ფიგურას). კვადრატი, რომელიც მოძრაობს კვადრატის სიბრტყის პერპენდიკულარული მიმართულებით, ქმნის კუბს (სამგანზომილებიანი ფიგურა).
კუბი, რომელიც მოძრაობს პერპენდიკულურად სამგანზომილებიანი სივრცის მიმართ, რომელშიც ის თავდაპირველად იყო განთავსებული, წარმოქმნის ჰიპერკუბს (ოთხგანზომილებიანი ფიგურა).
ჰიპერკუბის საზღვარი არის სამგანზომილებიანი, სასრული და დახურული. იგი შედგება სამგანზომილებიანი კუბისაგან საწყის მდგომარეობაში, სამგანზომილებიანი კუბისაგან ბოლო პოზიციაზე და ექვსი კუბისაგან, რომლებიც წარმოიქმნება თავდაპირველი კუბის კვადრატების მეოთხე განზომილების მიმართულებით გადაადგილებით. ჰიპერკუბის მთელი საზღვარი შედგება 8 სამგანზომილებიანი კუბისგან (უჯრედები).
საწყის პოზიციაზე გადაადგილებისას კუბს ჰქონდა 8 წვერო და ბოლო პოზიციაში ასევე 8 წვერო. ამრიგად, ჰიპერკუბს აქვს სულ 16 წვერო.
ოთხი ერთმანეთის პერპენდიკულური კიდე გამოდის თითოეული წვეროდან. ჰიპერკუბს სულ 32 კიდე აქვს.საწყის მდგომარეობაში მას ჰქონდა 12 კიდე, ბოლო პოზიციაში ასევე იყო 12 კიდე და მეოთხე განზომილებაში გადაადგილებისას კუბის წვეროებს ქმნიდა 8 კიდე.
ამრიგად, ჰიპერკუბის საზღვარი შედგება 8 კუბისგან, რომლებიც შედგება 24 კვადრატისგან. კერძოდ, 6 კვადრატი საწყის მდგომარეობაში, 6 ბოლო პოზიციაზე და 12 კვადრატი, რომელიც წარმოიქმნება 12 კიდეების გადაადგილებით მეოთხე განზომილების მიმართულებით.
გეომეტრიული მოდელი
ჰიპერკუბის დინამიური მოდელი შეიძლება არ ჩანდეს საკმარისად მკაფიო. ამიტომ, განიხილეთ ჰიპერკუბის გეომეტრიული მოდელი. როგორ მივიღოთ 3D კუბის გეომეტრიული მოდელი? ჩვენ ვაკეთებთ მის განვითარებას და განვითარების შედეგად ჩვენ "ერთად ვაწებებთ" კუბის მოდელს. სამგანზომილებიანი კუბის განვითარება შედგება კვადრატისაგან, რომლის გვერდებზე მიმაგრებულია კვადრატი პლუს კიდევ ერთი კვადრატი.  მეზობელ კვადრატებს ვატრიალებთ კვადრატის გვერდების ირგვლივ, კვადრატების მიმდებარე გვერდებს ვუკავშირებთ ერთმანეთს. დარჩენილ ოთხ მხარეს კი ბოლო კვადრატით ვხურავთ (სურ. 1).
მეზობელ კვადრატებს ვატრიალებთ კვადრატის გვერდების ირგვლივ, კვადრატების მიმდებარე გვერდებს ვუკავშირებთ ერთმანეთს. დარჩენილ ოთხ მხარეს კი ბოლო კვადრატით ვხურავთ (სურ. 1).
ანალოგიურად განვიხილოთ ჰიპერკუბის განვითარება. მისი განვითარება იქნება სამგანზომილებიანი ფიგურა, რომელიც შედგება ორიგინალური სამგანზომილებიანი კუბისაგან, ორიგინალური კუბის თითოეული სახის მიმდებარე ექვსი კუბისაგან და კიდევ ერთი კუბისაგან. სულ რვა სამგანზომილებიანი კუბია (ნახ. 2). ამ განვითარებისგან ოთხგანზომილებიანი კუბის (ჰიპერკუბის) მისაღებად, თქვენ უნდა მოატრიალოთ თითოეული მიმდებარე კუბი 90 გრადუსით. ეს მიმდებარე კუბურები განთავსდება განსხვავებულ სამგანზომილებიან სივრცეში. დააკავშირეთ კუბების მიმდებარე სახეები (კვადრატები) ერთმანეთთან. განათავსეთ მერვე კუბი თავისი სახეებით დარჩენილ ცარიელ ადგილას. ვიღებთ ოთხგანზომილებიან ფიგურას - ჰიპერკუბს, რომლის საზღვარი შედგება რვა სამგანზომილებიანი კუბისაგან.
ჰიპერკუბის გამოსახულება
 ზემოთ ნაჩვენები იყო, თუ როგორ უნდა "წებოთ" ჰიპერკუბის მოდელი სამგანზომილებიანი სკანირებიდან. ჩვენ ვიღებთ სურათებს პროექციის გამოყენებით. სამგანზომილებიანი კუბის ცენტრალური პროექცია (მისი გამოსახულება სიბრტყეზე) ასე გამოიყურება (ნახ. 3). კვადრატის შიგნით არის კიდევ ერთი კვადრატი. კვადრატის შესაბამისი წვეროები დაკავშირებულია სეგმენტებით. მიმდებარე კვადრატები გამოსახულია ტრაპეციის სახით, თუმცა სამგანზომილებიან სივრცეში ისინი კვადრატებია. შიდა და გარე კვადრატები სხვადასხვა ზომისაა, მაგრამ რეალურ სამგანზომილებიან სივრცეში ისინი თანაბარი კვადრატებია.
ზემოთ ნაჩვენები იყო, თუ როგორ უნდა "წებოთ" ჰიპერკუბის მოდელი სამგანზომილებიანი სკანირებიდან. ჩვენ ვიღებთ სურათებს პროექციის გამოყენებით. სამგანზომილებიანი კუბის ცენტრალური პროექცია (მისი გამოსახულება სიბრტყეზე) ასე გამოიყურება (ნახ. 3). კვადრატის შიგნით არის კიდევ ერთი კვადრატი. კვადრატის შესაბამისი წვეროები დაკავშირებულია სეგმენტებით. მიმდებარე კვადრატები გამოსახულია ტრაპეციის სახით, თუმცა სამგანზომილებიან სივრცეში ისინი კვადრატებია. შიდა და გარე კვადრატები სხვადასხვა ზომისაა, მაგრამ რეალურ სამგანზომილებიან სივრცეში ისინი თანაბარი კვადრატებია.
 ანალოგიურად, ოთხგანზომილებიანი კუბის ცენტრალური პროექცია სამგანზომილებიან სივრცეზე ასე გამოიყურება: ერთი კუბის შიგნით არის მეორე კუბი. კუბების შესაბამისი წვერები დაკავშირებულია სეგმენტებით. შიდა და გარე კუბებს აქვთ სხვადასხვა ზომის სამგანზომილებიანი სივრცე, მაგრამ ოთხგანზომილებიან სივრცეში ისინი თანაბარი კუბურებია (ნახ. 4).
ანალოგიურად, ოთხგანზომილებიანი კუბის ცენტრალური პროექცია სამგანზომილებიან სივრცეზე ასე გამოიყურება: ერთი კუბის შიგნით არის მეორე კუბი. კუბების შესაბამისი წვერები დაკავშირებულია სეგმენტებით. შიდა და გარე კუბებს აქვთ სხვადასხვა ზომის სამგანზომილებიანი სივრცე, მაგრამ ოთხგანზომილებიან სივრცეში ისინი თანაბარი კუბურებია (ნახ. 4).
ექვსი დამსხვრეული პირამიდა არის ოთხგანზომილებიანი კუბის ტოლი ექვსი უჯრედის (კუბის) გამოსახულება.
ეს სამგანზომილებიანი პროექცია შეიძლება დახატოს სიბრტყეზე და დადასტურდეს, რომ დინამიური მოდელის გამოყენებით მიღებული ჰიპერკუბის თვისებები შეესაბამება სიმართლეს.
ჰიპერკუბს აქვს 16 წვერო, 32 კიდე, 24 სახე (კვადრატი), 8 უჯრედი (კუბი). ოთხი ერთმანეთის პერპენდიკულური კიდე გამოდის თითოეული წვეროდან. ჰიპერკუბის საზღვარი არის სამგანზომილებიანი დახურული ამოზნექილი ფიგურა, რომლის მოცულობა (ჰიპერკუბის გვერდითი მოცულობა) რვა ერთეული სამგანზომილებიანი კუბის ტოლია. თავის შიგნით ეს ფიგურა შეიცავს ერთეულ ჰიპერკუბს, რომლის ჰიპერმოცულობის ტოლია ერთეული ჰიპერკუბის ჰიპერმოცულობის.
დასკვნა
ამ სამუშაოს მიზანი იყო ოთხგანზომილებიანი სივრცის თავდაპირველი გაცნობა. ეს გაკეთდა უმარტივესი ფიგურის - ჰიპერკუბის მაგალითის გამოყენებით.
ოთხგანზომილებიანი სივრცის სამყარო საოცარია! მასში, სამგანზომილებიან სივრცეში მსგავს ფიგურებთან ერთად, არის ფიგურებიც, რომლებსაც ანალოგი არ აქვთ სამგანზომილებიან სივრცეში.
მატერიალური სამყაროს მრავალი ფენომენი, მაკროსამყარო და მეგასამყარო, მიუხედავად უზარმაზარი წარმატებებისა ფიზიკაში, ქიმიასა და ასტრონომიაში, აუხსნელი დარჩა.
არ არსებობს ერთი თეორია, რომელიც ხსნის ბუნების ყველა ძალას. არ არსებობს სამყაროს დამაკმაყოფილებელი მოდელი, რომელიც ხსნის მის სტრუქტურას და გამორიცხავს პარადოქსებს.
ოთხგანზომილებიანი სივრცის თვისებების შესწავლით და ოთხგანზომილებიანი გეომეტრიიდან იდეების ნასესხებით, შესაძლებელი იქნება არა მხოლოდ მატერიალური სამყაროს უფრო მკაცრი თეორიებისა და მოდელების აგება, არამედ ინსტრუმენტებისა და სისტემების შექმნა, რომლებიც მოქმედებენ კანონების შესაბამისად. ოთხგანზომილებიანი სამყაროს, მაშინ ადამიანის შესაძლებლობები კიდევ უფრო შთამბეჭდავი იქნება.
ბაკალიარ მარია
შესწავლილია ოთხგანზომილებიანი კუბის ცნების (ტესერაქტის) დანერგვის მეთოდები, მისი სტრუქტურა და ზოგიერთი თვისება.. კითხვა, თუ რა სამგანზომილებიანი ობიექტები მიიღება ოთხგანზომილებიანი კუბის სამგანზომილებიანი სახეების პარალელურად ჰიპერთპნებით გადაკვეთისას. , ასევე მიმართულია მისი მთავარი დიაგონალის პერპენდიკულარული ჰიპერთრემნებით. განხილულია კვლევისთვის გამოყენებული მრავალგანზომილებიანი ანალიტიკური გეომეტრიის აპარატი.
ჩამოტვირთვა:
გადახედვა:
შესავალი ………………………………………………………………………………………….2
ძირითადი ნაწილი ……………………………………………………………..4
დასკვნები ……………………………………………………………………………………………………………………………………………………………………
გამოყენებული ლიტერატურა………………………………………………………………..13
შესავალი
ოთხგანზომილებიანი სივრცე დიდი ხანია მიიპყრო როგორც პროფესიონალი მათემატიკოსების, ისე ამ მეცნიერების შესწავლისგან შორს მყოფი ადამიანების ყურადღებას. მეოთხე განზომილებისადმი ინტერესი შეიძლება გამოწვეული იყოს იმ ვარაუდით, რომ ჩვენი სამგანზომილებიანი სამყარო არის „ჩაძირული“ ოთხგანზომილებიან სივრცეში, ისევე როგორც თვითმფრინავი არის „ჩაძირული“ სამგანზომილებიან სივრცეში, სწორი ხაზი არის „ჩაძირული“ სიბრტყე, და წერტილი არის სწორი ხაზი. გარდა ამისა, ოთხგანზომილებიანი სივრცე მნიშვნელოვან როლს ასრულებს ფარდობითობის თანამედროვე თეორიაში (ე.წ. სივრცე-დრო ან მინკოვსკის სივრცე) და ასევე შეიძლება ჩაითვალოს განსაკუთრებულ შემთხვევად.განზომილებიანი ევკლიდური სივრცე (ერთად).
ოთხგანზომილებიანი კუბი (ტესერაქტი) არის ობიექტი ოთხგანზომილებიან სივრცეში, რომელსაც აქვს მაქსიმალური შესაძლო განზომილება (ისევე, როგორც ჩვეულებრივი კუბი არის ობიექტი სამგანზომილებიან სივრცეში). გაითვალისწინეთ, რომ ის ასევე პირდაპირ ინტერესს იწვევს, კერძოდ, ის შეიძლება გამოჩნდეს წრფივი პროგრამირების ოპტიმიზაციის ამოცანებში (როგორც ზონა, რომელშიც ნაპოვნია ოთხი ცვლადის წრფივი ფუნქციის მინიმალური ან მაქსიმუმი), ასევე გამოიყენება ციფრულ მიკროელექტრონიკაში (როდესაც ელექტრონული საათის დისპლეის მუშაობის პროგრამირება). გარდა ამისა, ოთხგანზომილებიანი კუბის შესწავლის პროცესი ხელს უწყობს სივრცითი აზროვნებისა და წარმოსახვის განვითარებას.
შესაბამისად, საკმაოდ აქტუალურია ოთხგანზომილებიანი კუბის სტრუქტურისა და სპეციფიკური თვისებების შესწავლა. აღსანიშნავია, რომ სტრუქტურული თვალსაზრისით, ოთხგანზომილებიანი კუბი საკმაოდ კარგად არის შესწავლილი. ბევრად უფრო საინტერესოა მისი მონაკვეთების ბუნება სხვადასხვა ჰიპერთვითმფრინავით. ამგვარად, ამ ნაშრომის მთავარი მიზანია ტესერაქტის სტრუქტურის შესწავლა, ასევე, გარკვევა, თუ რა სამგანზომილებიანი ობიექტები მიიღება, თუ ოთხგანზომილებიანი კუბი დაიშლება ჰიპერთვითმფრინავებით, პარალელურად მისი სამიდან. განზომილებიანი სახეები, ან მისი მთავარი დიაგონალის პერპენდიკულარული ჰიპერპლანტებით. ოთხგანზომილებიან სივრცეში ჰიპერთვითმფრინავას სამგანზომილებიანი ქვესივრცე ეწოდება. შეგვიძლია ვთქვათ, რომ სიბრტყეზე სწორი ხაზი არის ერთგანზომილებიანი ჰიპერთვითმფრინავი, სიბრტყე სამგანზომილებიან სივრცეში არის ორგანზომილებიანი ჰიპერთვითმფრინავი.
მიზანი განსაზღვრავდა კვლევის მიზნებს:
1) მრავალგანზომილებიანი ანალიტიკური გეომეტრიის ძირითადი ფაქტების შესწავლა;
2) 0-დან 3-მდე ზომების კუბების აგების თავისებურებების შესწავლა;
3) ოთხგანზომილებიანი კუბის სტრუქტურის შესწავლა;
4) ანალიტიკურად და გეომეტრიულად აღწერეთ ოთხგანზომილებიანი კუბი;
5) სამგანზომილებიანი და ოთხგანზომილებიანი კუბების განვითარებისა და ცენტრალური პროგნოზების მოდელების შედგენა.
6) მრავალგანზომილებიანი ანალიტიკური გეომეტრიის აპარატის გამოყენებით, აღწერეთ სამგანზომილებიანი ობიექტები, რომლებიც წარმოიქმნება ოთხგანზომილებიანი კუბის გადაკვეთის შედეგად მისი ერთ-ერთი სამგანზომილებიანი პირის პარალელურად ჰიპერთვითმგებლებთან ან მის მთავარ დიაგონალზე პერპენდიკულარულ ჰიპერთპინებთან.
ამ გზით მიღებული ინფორმაცია საშუალებას მოგვცემს უკეთ გავიგოთ ტეზერაქტის სტრუქტურა, ასევე დავადგინოთ ღრმა ანალოგიები სხვადასხვა განზომილების კუბების სტრუქტურასა და თვისებებში.
Მთავარი ნაწილი
პირველ რიგში, ჩვენ აღვწერთ მათემატიკურ აპარატს, რომელსაც გამოვიყენებთ ამ კვლევის დროს.
1) ვექტორული კოორდინატები: თუ, ეს
2) ჰიპერთვითმფრინავის განტოლება ნორმალური ვექტორითჰგავს აქ
3) თვითმფრინავები და პარალელურები არიან თუ და მხოლოდ თუ
4) მანძილი ორ წერტილს შორის განისაზღვრება შემდეგნაირად: თუ, ეს
5) ვექტორების ორთოგონალურობის პირობა:
უპირველეს ყოვლისა, მოდით გავარკვიოთ, როგორ აღვწეროთ ოთხგანზომილებიანი კუბი. ეს შეიძლება გაკეთდეს ორი გზით - გეომეტრიული და ანალიტიკური.
თუ ვსაუბრობთ დაზუსტების გეომეტრიულ მეთოდზე, მაშინ მიზანშეწონილია თვალყური ადევნოთ კუბების აგების პროცესს, დაწყებული ნულოვანი განზომილებიდან. ნულოვანი განზომილების კუბი არის წერტილი (გაითვალისწინეთ, სხვათა შორის, რომ წერტილს შეუძლია ნულოვანი განზომილების ბურთის როლიც შეასრულოს). შემდეგი, ჩვენ წარმოვადგენთ პირველ განზომილებას (x-ღერძი) და შესაბამის ღერძზე ვნიშნავთ ორ წერტილს (ორი ნულოვანი განზომილებიანი კუბი), რომლებიც მდებარეობს ერთმანეთისგან 1 მანძილზე. შედეგი არის სეგმენტი - ერთგანზომილებიანი კუბი. დაუყოვნებლივ აღვნიშნოთ დამახასიათებელი თვისება: ერთგანზომილებიანი კუბის (სეგმენტის) საზღვარი (ბოლოები) არის ორი ნულოვანი განზომილებიანი კუბი (ორი წერტილი). შემდეგი, ჩვენ ვაცნობთ მეორე განზომილებას (ორდინატთა ღერძი) და სიბრტყეზეავაშენოთ ორი ერთგანზომილებიანი კუბი (ორი სეგმენტი), რომელთა ბოლოები ერთმანეთისგან 1-ით არის დაშორებული (სინამდვილეში, ერთი სეგმენტი მეორის ორთოგონალური პროექციაა). სეგმენტების შესაბამისი ბოლოების შეერთებით ვიღებთ კვადრატს - ორგანზომილებიან კუბს. კიდევ ერთხელ გაითვალისწინეთ, რომ ორგანზომილებიანი კუბის (კვადრატის) საზღვარი არის ოთხი ერთგანზომილებიანი კუბი (ოთხი სეგმენტი). და ბოლოს, ჩვენ შემოგვაქვს მესამე განზომილება (გამოიყენეთ ღერძი) და ვაშენებთ სივრცეშიორი კვადრატი ისე, რომ ერთი მათგანი მეორის ორთოგონალური პროექცია იყოს (კვადრატების შესაბამისი წვეროები ერთმანეთისგან 1-ის მანძილზეა). შევაერთოთ შესაბამისი წვეროები სეგმენტებთან - მივიღებთ სამგანზომილებიან კუბს. ჩვენ ვხედავთ, რომ სამგანზომილებიანი კუბის საზღვარი არის ექვსი ორგანზომილებიანი კუბი (ექვსი კვადრატი). აღწერილი კონსტრუქციები საშუალებას გვაძლევს განვსაზღვროთ შემდეგი ნიმუში: ყოველ საფეხურზეგანზომილებიანი კუბი "მოძრაობს და ტოვებს კვალს".გაზომვა 1-ის მანძილზე, ხოლო მოძრაობის მიმართულება კუბის პერპენდიკულარულია. ეს არის ამ პროცესის ფორმალური გაგრძელება, რომელიც საშუალებას გვაძლევს მივიდეთ ოთხგანზომილებიანი კუბის კონცეფციამდე. სახელდობრ, სამგანზომილებიან კუბს ვაიძულებთ გადავიდეს მეოთხე განზომილების (კუბის პერპენდიკულარულად) მიმართულებით 1 მანძილით. ვიმოქმედოთ წინას ანალოგიურად, ანუ კუბების შესაბამისი წვეროების შეერთებით, მივიღებთ ოთხგანზომილებიან კუბს. უნდა აღინიშნოს, რომ გეომეტრიულად ასეთი კონსტრუქცია ჩვენს სივრცეში შეუძლებელია (რადგან ის სამგანზომილებიანია), მაგრამ აქ ლოგიკური თვალსაზრისით წინააღმდეგობებს არ ვაწყდებით. ახლა გადავიდეთ ოთხგანზომილებიანი კუბის ანალიტიკურ აღწერაზე. იგი ასევე მიიღება ფორმალურად, ანალოგიის გამოყენებით. ასე რომ, ნულოვანი განზომილებიანი ერთეული კუბის ანალიზურ სპეციფიკაციას აქვს ფორმა:
ერთგანზომილებიანი ერთეული კუბის ანალიზურ ამოცანას აქვს ფორმა:
ორგანზომილებიანი ერთეული კუბის ანალიტიკურ ამოცანას აქვს ფორმა:
სამგანზომილებიანი ერთეული კუბის ანალიტიკურ ამოცანას აქვს ფორმა:
ახლა ძალიან ადვილია ოთხგანზომილებიანი კუბის ანალიტიკური წარმოდგენის მიცემა, კერძოდ:
როგორც ვხედავთ, ოთხგანზომილებიანი კუბის განსაზღვრის როგორც გეომეტრიული, ასევე ანალიტიკური მეთოდები იყენებდნენ ანალოგიების მეთოდს.
ახლა, ანალიტიკური გეომეტრიის აპარატის გამოყენებით, გავარკვევთ, რა სტრუქტურა აქვს ოთხგანზომილებიან კუბს. პირველ რიგში, მოდით გავარკვიოთ, რა ელემენტებს შეიცავს იგი. აქ კვლავ შეგვიძლია გამოვიყენოთ ანალოგია (ჰიპოთეზის დასაყენებლად). ერთგანზომილებიანი კუბის საზღვრებია წერტილები (ნულგანზომილებიანი კუბურები), ორგანზომილებიანი კუბის - სეგმენტები (ერთგანზომილებიანი კუბურები), სამგანზომილებიანი კუბის - კვადრატები (ორგანზომილებიანი სახეები). შეიძლება ვივარაუდოთ, რომ ტესერაქტის საზღვრები არის სამგანზომილებიანი კუბურები. ამის დასამტკიცებლად განვმარტოთ რას ნიშნავს წვეროები, კიდეები და სახეები. კუბის წვეროები მისი კუთხის წერტილებია. ანუ წვეროების კოორდინატები შეიძლება იყოს ნულები ან ერთი. ამრიგად, ვლინდება კავშირი კუბის განზომილებასა და მის წვეროების რაოდენობას შორის. მოდით გამოვიყენოთ კომბინატორიული პროდუქტის წესი - წვეროდანგაზომილი კუბი ზუსტად აქვსკოორდინატები, რომელთაგან თითოეული ტოლია ნულის ან ერთის (ყველა დანარჩენისგან დამოუკიდებელი), მაშინ მთლიანობაში არისმწვერვალები ამრიგად, ნებისმიერი წვეროსთვის ყველა კოორდინატი ფიქსირდება და შეიძლება იყოს ტოლიან . თუ დავაფიქსირებთ ყველა კოორდინატს (თითოეული მათგანის თანაბარიან , განურჩევლად სხვებისა), გარდა ერთისა, ვიღებთ სწორ ხაზებს, რომლებიც შეიცავს კუბის კიდეებს. წინას მსგავსად, შეგიძლიათ დათვალოთ, რომ არსებობენ ზუსტადრამ. და თუ ახლა დავაფიქსირებთ ყველა კოორდინატს (თითოეული მათგანის თანაბარიან , სხვებისგან დამოუკიდებლად), ორის გარდა, ვიღებთ სიბრტყეებს, რომლებიც შეიცავს კუბის ორგანზომილებიან სახეებს. კომბინატორიკის წესის გამოყენებით აღმოვაჩენთ, რომ არსებობს ზუსტადრამ. შემდეგი, ანალოგიურად - ყველა კოორდინატის დაფიქსირება (თითოეული მათგანის თანაბარი დაყენებაან , დანარჩენებისგან დამოუკიდებლად), სამის გარდა, ვიღებთ ჰიპერთრემონებს, რომლებიც შეიცავს კუბის სამგანზომილებიან სახეებს. იგივე წესით ვიანგარიშებთ მათ რაოდენობას - ზუსტადდა ა.შ. ეს საკმარისი იქნება ჩვენი კვლევისთვის. მოდით მივიღოთ მიღებული შედეგები ოთხგანზომილებიანი კუბის სტრუქტურაზე, კერძოდ, ყველა წარმოებულ ფორმულაში, რომელსაც ჩვენ ვაყენებთ.. ამრიგად, ოთხგანზომილებიან კუბს აქვს: 16 წვერო, 32 კიდე, 24 ორგანზომილებიანი სახე და 8 სამგანზომილებიანი სახე. სიცხადისთვის, მოდით განვსაზღვროთ ანალიტიკურად მისი ყველა ელემენტი.
ოთხგანზომილებიანი კუბის წვეროები:
ოთხგანზომილებიანი კუბის კიდეები ():
ოთხგანზომილებიანი კუბის ორგანზომილებიანი სახეები (მსგავსი შეზღუდვები):
ოთხგანზომილებიანი კუბის სამგანზომილებიანი სახეები (მსგავსი შეზღუდვები):
ახლა, როდესაც ოთხგანზომილებიანი კუბის სტრუქტურა და მისი განსაზღვრის მეთოდები საკმარისად დეტალურად არის აღწერილი, მოდით გადავიდეთ მთავარი მიზნის განხორციელებაზე - კუბის სხვადასხვა მონაკვეთების ბუნების გარკვევა. დავიწყოთ ელემენტარული შემთხვევით, როდესაც კუბის მონაკვეთები მისი ერთ-ერთი სამგანზომილებიანი სახის პარალელურია. მაგალითად, განიხილეთ მისი მონაკვეთები სახის პარალელურად ჰიპერპლანტებითანალიტიკური გეომეტრიიდან ცნობილია, რომ ნებისმიერი ასეთი მონაკვეთი მოცემულია განტოლებითმოდით განვსაზღვროთ შესაბამისი სექციები ანალიტიკურად:
როგორც ვხედავთ, ჩვენ მივიღეთ ანალიტიკური სპეციფიკაცია სამგანზომილებიანი ერთეული კუბისთვის, რომელიც მდებარეობს ჰიპერთვითმფრინავში.
ანალოგიის დასამყარებლად დავწეროთ სამგანზომილებიანი კუბის მონაკვეთი სიბრტყითჩვენ ვიღებთ:
ეს არის კვადრატი, რომელიც დევს თვითმფრინავში. ანალოგია აშკარაა.
ოთხგანზომილებიანი კუბის მონაკვეთები ჰიპერპლანტებითიძლევა სრულიად მსგავს შედეგებს. ეს ასევე იქნება ერთჯერადი სამგანზომილებიანი კუბურები, რომლებიც დევს ჰიპერთვითმფრინავებშიშესაბამისად.
ახლა განვიხილოთ ოთხგანზომილებიანი კუბის მონაკვეთები მისი მთავარი დიაგონალის პერპენდიკულარული ჰიპერთრემბებით. ჯერ ეს პრობლემა მოვაგვაროთ სამგანზომილებიანი კუბისთვის. ერთეული სამგანზომილებიანი კუბის განსაზღვრის ზემოთ აღწერილი მეთოდის გამოყენებით, ის ასკვნის, რომ მთავარ დიაგონალად შეიძლება ავიღოთ, მაგალითად, ბოლოებით სეგმენტი.და . ეს ნიშნავს, რომ მთავარი დიაგონალის ვექტორს ექნება კოორდინატები. ამრიგად, ნებისმიერი სიბრტყის განტოლება მთავარ დიაგონალზე პერპენდიკულარული იქნება:
მოდით განვსაზღვროთ პარამეტრების ცვლილების საზღვრები. იმიტომ რომ , მაშინ ამ უტოლობების ტერმინებით ვამატებით მივიღებთ:
ან .
თუ, მაშინ (შეზღუდვების გამო). ანალოგიურად - თუ, რომ . ასე რომ, როდის და როდის საჭრელ სიბრტყეს და კუბს აქვთ ზუსტად ერთი საერთო წერტილი (და შესაბამისად). ახლა აღვნიშნოთ შემდეგი. თუ(ისევ ცვლადი შეზღუდვების გამო). შესაბამისი სიბრტყეები ერთდროულად კვეთენ სამ სახეს, რადგან, წინააღმდეგ შემთხვევაში, ჭრის სიბრტყე პარალელურად იქნებოდა ერთ-ერთი მათგანის, რაც არ ხდება მდგომარეობის მიხედვით. თუ, მაშინ თვითმფრინავი კვეთს კუბის ყველა სახეს. თუ, მაშინ თვითმფრინავი კვეთს სახეებს. წარმოგიდგენთ შესაბამის გამოთვლებს.
დაე მერე თვითმფრინავიხაზს კვეთსსწორ ხაზზე და. ზღვარი, უფრო მეტიც. ზღვარი თვითმფრინავი იკვეთება სწორ ხაზზე, და
დაე მერე თვითმფრინავიკვეთს ხაზს:
კიდე სწორი ხაზით და .
კიდე სწორი ხაზით და .
კიდე სწორი ხაზით და .
კიდე სწორი ხაზით და .
კიდე სწორი ხაზით და .
კიდე სწორი ხაზით და .
ამჯერად ვიღებთ ექვს სეგმენტს, რომლებსაც თანმიმდევრულად საერთო ბოლოები აქვთ:
დაე მერე თვითმფრინავიხაზს კვეთსსწორ ხაზზე და. ზღვარი თვითმფრინავი იკვეთება სწორ ხაზზე, და . ზღვარი თვითმფრინავი იკვეთება სწორ ხაზზე, და . ანუ, ჩვენ ვიღებთ სამ სეგმენტს, რომლებსაც აქვთ წყვილი საერთო ბოლოები:ამრიგად, მითითებული პარამეტრის მნიშვნელობებისთვისთვითმფრინავი გადაკვეთს კუბს რეგულარული სამკუთხედის გასწვრივ წვეროებით
ასე რომ, აქ არის ყოვლისმომცველი აღწერა სიბრტყის ფიგურებისა, რომლებიც მიიღება, როდესაც კუბი იკვეთება მისი მთავარი დიაგონალის პერპენდიკულარული სიბრტყით. მთავარი იდეა ასეთი იყო. აუცილებელია იმის გაგება, თუ რომელ სახეებს კვეთს სიბრტყე, რომელი სიმრავლის გასწვრივ კვეთს მათ და როგორ არის დაკავშირებული ეს სიმრავლეები ერთმანეთთან. მაგალითად, თუ აღმოჩნდა, რომ სიბრტყე კვეთს ზუსტად სამ სახეს სეგმენტების გასწვრივ, რომლებსაც აქვთ წყვილი საერთო ბოლოები, მაშინ მონაკვეთი არის ტოლგვერდა სამკუთხედი (რაც დასტურდება სეგმენტების სიგრძის პირდაპირ გამოთვლით), რომლის წვეროები არის ეს ბოლოები. სეგმენტების.
ერთი და იგივე აპარატის გამოყენებით და სექციების შესწავლის იგივე იდეით, შემდეგი ფაქტების დასკვნა შესაძლებელია სრულიად ანალოგიურად:
1) ოთხგანზომილებიანი ერთეული კუბის ერთ-ერთი მთავარი დიაგონალის ვექტორს აქვს კოორდინატები
2) ოთხგანზომილებიანი კუბის მთავარ დიაგონალზე პერპენდიკულარული ნებისმიერი ჰიპერპლანე შეიძლება დაიწეროს სახით.
3) სეკანტური ჰიპერპლანის განტოლებაში პარამეტრიშეიძლება განსხვავდებოდეს 0-დან 4-მდე;
4) როდის და სეკანტურ ჰიპერპლანეტსა და ოთხგანზომილებიან კუბს ერთი საერთო წერტილი აქვთ (და შესაბამისად);
5) როდის განივი კვეთა გამოიმუშავებს რეგულარულ ტეტრაედრონს;
6) როდის განივი მონაკვეთში შედეგი იქნება ოქტაედონი;
7) როდის განივი მონაკვეთი გამოიმუშავებს რეგულარულ ტეტრაედრონს.
შესაბამისად, აქ ჰიპერსიბრტყე კვეთს ტესერაქტს სიბრტყის გასწვრივ, რომელზედაც, ცვლადების შეზღუდვის გამო, გამოყოფილია სამკუთხა რეგიონი (ანალოგია - სიბრტყე კვეთს კუბს სწორი ხაზის გასწვრივ, რომელზედაც, შეზღუდვების გამო ცვლადები, გამოყოფილი იყო სეგმენტი). 5 შემთხვევაში) ჰიპერპლანე კვეთს ტესერაქტის ზუსტად ოთხ სამგანზომილებიან სახეს, ანუ მიიღება ოთხი სამკუთხედი, რომლებსაც აქვთ წყვილი საერთო გვერდები, სხვა სიტყვებით რომ ვთქვათ, ქმნიან ტეტრაედრონს (როგორ შეიძლება გამოვთვალოთ ეს არის სწორი). მე-6 შემთხვევაში ჰიპერთვითმფრინავი კვეთს ტესერაქტის ზუსტად რვა სამგანზომილებიან სახეს, ანუ მიიღება რვა სამკუთხედი, რომლებსაც აქვთ თანმიმდევრულად საერთო გვერდები, სხვა სიტყვებით რომ ვთქვათ, ქმნიან ოქტაედრონს. შემთხვევა 7) სრულიად ჰგავს მე-5 შემთხვევას).
მოდით, ეს კონკრეტული მაგალითით ავხსნათ. კერძოდ, ჩვენ ვსწავლობთ ოთხგანზომილებიანი კუბის მონაკვეთს ჰიპერთვითმფრინავითცვლადი შეზღუდვების გამო, ეს ჰიპერპლანე კვეთს შემდეგ სამგანზომილებიან სახეებს:ზღვარი კვეთს სიბრტყის გასწვრივცვლადების შეზღუდვების გამო, ჩვენ გვაქვს:ვიღებთ სამკუთხა ფართობს წვეროებითᲣფრო,ვიღებთ სამკუთხედსროდესაც ჰიპერთვითმფრინავი კვეთს სახესვიღებთ სამკუთხედსროდესაც ჰიპერთვითმფრინავი კვეთს სახესვიღებთ სამკუთხედსამრიგად, ტეტრაედრის წვეროებს აქვთ შემდეგი კოორდინატები. როგორც ადვილი გამოსათვლელია, ეს ტეტრაედონი მართლაც რეგულარულია.
დასკვნები
ამრიგად, ამ კვლევის პროცესში შეისწავლეს მრავალგანზომილებიანი ანალიტიკური გეომეტრიის ძირითადი ფაქტები, შეისწავლეს 0-დან 3-მდე განზომილებების კუბების აგების თავისებურებები, შეისწავლეს ოთხგანზომილებიანი კუბის სტრუქტურა, ოთხგანზომილებიანი კუბი. ანალიტიკურად და გეომეტრიულად იყო აღწერილი, გაკეთდა სამგანზომილებიანი და ოთხგანზომილებიანი კუბების განვითარების მოდელები და ცენტრალური პროგნოზები, სამგანზომილებიანი კუბურები ანალიტიკურად იყო აღწერილი ობიექტები, რომლებიც წარმოიქმნება ოთხგანზომილებიანი კუბის გადაკვეთის შედეგად ჰიპერთრემბებთან, რომლებიც პარალელურად იყო მისი სამგანზომილებიანი. განზომილებიანი სახეები, ან მისი მთავარი დიაგონალის პერპენდიკულარული ჰიპერთრემნებით.
ჩატარებულმა კვლევამ შესაძლებელი გახადა ღრმა ანალოგიების გამოვლენა სხვადასხვა განზომილების კუბების სტრუქტურასა და თვისებებში. გამოყენებული ანალოგიის ტექნიკა შეიძლება გამოყენებულ იქნას კვლევაში, მაგალითად,განზომილებიანი სფერო ანგანზომილებიანი მარტივი. კერძოდ,განზომილებიანი სფერო შეიძლება განისაზღვროს, როგორც წერტილების ნაკრებიმოცემული წერტილიდან თანაბარი განზომილებიანი სივრცე, რომელსაც სფეროს ცენტრს უწოდებენ. Უფრო,განზომილებიანი სიმპლექსი შეიძლება განისაზღვროს, როგორც ნაწილიგანზომილებიანი სივრცე შეზღუდულია მინიმალური რაოდენობითგანზომილებიანი ჰიპერპლანტები. მაგალითად, ერთგანზომილებიანი სიმპლექსი არის სეგმენტი (ერთგანზომილებიანი სივრცის ნაწილი, შემოიფარგლება ორი წერტილით), ორგანზომილებიანი მარტივი არის სამკუთხედი (ორგანზომილებიანი სივრცის ნაწილი, შემოიფარგლება სამი ხაზით), სამგანზომილებიანი მარტივი არის ტეტრაედონი (სამგანზომილებიანი სივრცის ნაწილი, რომელიც შემოიფარგლება ოთხი სიბრტყით). ბოლოს და ბოლოს,ჩვენ განვსაზღვრავთ განზომილებიანი სიმპლექსს, როგორც ნაწილსგანზომილებიანი სივრცე, შეზღუდულიგანზომილების ჰიპერპლანი.
გაითვალისწინეთ, რომ ტესერაქტის მრავალრიცხოვანი გამოყენების მიუხედავად მეცნიერების ზოგიერთ სფეროში, ეს კვლევა მაინც ძირითადად მათემატიკური კვლევაა.
ბიბლიოგრაფია
1) ბუგროვი ია.ს., ნიკოლსკი ს.მ.უმაღლესი მათემატიკა, ტ.1 – M.: Bustard, 2005 – 284 გვ.
2) კვანტური. ოთხგანზომილებიანი კუბი / Duzhin S., Rubtsov V., No6, 1986 წ.
3) კვანტური. Როგორ დავხატო განზომილებიანი კუბი / Demidovich N.B., No8, 1974 წ.









