Znajdowanie pochodnej danej funkcji f nazywa się. Pochodna e do potęgi x i funkcji wykładniczej

Na tej lekcji nauczymy się stosować wzory i reguły różniczkowania.

Przykłady. Znajdź pochodne funkcji.

1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Stosowanie reguły I, formuły 4, 2 i 1. Otrzymujemy:

y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.

2. y=3x 6 -2x+5. Rozwiązujemy podobnie, używając tych samych wzorów i formuł 3.

y’=3∙6x 5 -2=18x 5 -2.

Stosowanie reguły I, formuły 3, 5 I 6 I 1.

Stosowanie reguły IV, formuły 5 I 1 .

W piątym przykładzie zgodnie z regułą I pochodna sumy jest równa sumie pochodnych i właśnie znaleźliśmy pochodną pierwszego wyrazu (przykład 4 ), zatem znajdziemy pochodne 2 I 3 warunki i za 1 podsumowując, możemy od razu zapisać wynik.

Rozróżniajmy 2 I 3 wyrazy zgodnie ze wzorem 4 . W tym celu przekształcamy pierwiastki potęgi trzeciej i czwartej w mianownikach na potęgi o wykładnikach ujemnych, a następnie zgodnie z 4 wzór, znajdujemy pochodne potęg.

Spójrz na ten przykład i wynik. Złapałeś wzór? Cienki. Oznacza to, że mamy nową formułę i możemy ją dodać do naszej tabeli instrumentów pochodnych.

Rozwiążmy szósty przykład i wyprowadźmy inną formułę.

Skorzystajmy z reguły IV i formuła 4 . Skróćmy powstałe ułamki.

Przyjrzyjmy się tej funkcji i jej pochodnej. Oczywiście rozumiesz wzór i jesteś gotowy nazwać formułę:

Nauka nowych formuł!

Przykłady.

1. Znajdź przyrost argumentu i przyrost funkcji y= x 2, jeśli początkowa wartość argumentu była równa 4 , i nowy - 4,01 .

Rozwiązanie.

Nowa wartość argumentu x=x 0 +Δx. Podstawmy dane: 4,01=4+Δх, stąd przyrost argumentu Δх=4,01-4=0,01. Przyrost funkcji z definicji jest równy różnicy między nową i poprzednią wartością funkcji, tj. Δy=f (x 0 + Δx) - f (x 0). Ponieważ mamy funkcję y=x2, To Δу=(x 0 +Δx) 2 - (x 0) 2 =(x 0) 2 +2x 0 · Δx+(Δx) 2 - (x 0) 2 =2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Odpowiedź: przyrost argumentu Δх=0,01; przyrost funkcji Δу=0,0801.

Przyrost funkcji można znaleźć inaczej: Δy=y (x 0 +Δx) -y (x 0)=y(4,01) -y(4)=4,01 2 -4 2 =16,0801-16=0,0801.

2. Znajdź kąt nachylenia stycznej do wykresu funkcji y=f(x) w tym punkcie x 0, Jeśli fa "(x 0) = 1.

Rozwiązanie.

Wartość pochodnej w punkcie styczności x 0 i jest wartością tangensa kąta stycznego (geometryczne znaczenie pochodnej). Mamy: f "(x 0) = tanα = 1 → α = 45°, ponieważ tg45°=1.

Odpowiedź: styczna do wykresu tej funkcji tworzy kąt z dodatnim kierunkiem osi Ox równym 45°.

3. Wyprowadź wzór na pochodną funkcji y=xn.

Różnicowanie jest działaniem polegającym na znalezieniu pochodnej funkcji.

Szukając pochodnych, należy stosować wzory, które wyprowadzono na podstawie definicji pochodnej, w taki sam sposób, w jaki wyprowadziliśmy wzór na stopień pochodnej: (x n)" = nx n-1.

To są formuły.

Tabela instrumentów pochodnychŁatwiej będzie zapamiętać, wymawiając sformułowania słowne:

1. Pochodna wielkości stałej wynosi zero.

2. X liczba pierwsza jest równa jeden.

3. Ze znaku pochodnej można odjąć stały współczynnik.

4. Pochodna stopnia jest równa iloczynowi wykładnika tego stopnia przez stopień o tej samej podstawie, ale wykładnik jest o jeden mniejszy.

5. Pochodna pierwiastka jest równa jedności podzielonej przez dwa równe pierwiastki.

6. Pochodna jedności podzielona przez x jest równa minus jeden podzielona przez x do kwadratu.

7. Pochodna sinusa jest równa cosinusowi.

8. Pochodna cosinusa jest równa minus sinus.

9. Pochodna tangensa jest równa jedności podzielonej przez kwadrat cosinusa.

10. Pochodna cotangensa jest równa minus jeden podzielona przez kwadrat sinusa.

Uczymy zasady różnicowania.

1. Pochodna sumy algebraicznej jest równa sumie algebraicznej pochodnych wyrazów.

2. Pochodna iloczynu jest równa iloczynowi pochodnej pierwszego czynnika i drugiego czynnika plus iloczyn pierwszego czynnika i pochodnej drugiego.

3. Pochodna „y” podzielona przez „ve” jest równa ułamkowi, w którym licznikiem jest „y liczba pierwsza pomnożona przez „ve” minus „y pomnożona przez ve liczba pierwsza”, a mianownikiem jest „ve kwadrat”.

4. Szczególny przypadek formuły 3.

Uczmy się razem!

Strona 1 z 1 1

Przy rozwiązywaniu różnych problemów geometrii, mechaniki, fizyki i innych dziedzin wiedzy pojawiła się potrzeba wykorzystania tego samego procesu analitycznego z tej funkcji y=f(x) uzyskać nową funkcję o nazwie funkcja pochodna(lub po prostu pochodna) danej funkcji f(x) i jest oznaczony symbolem

Proces, w wyniku którego z danej funkcji k(x) uzyskać nową funkcję f” (x), zwany różnicowanie i składa się z trzech następujących kroków: 1) podać argument X przyrost  X i wyznacz odpowiedni przyrost funkcji  y = f(x+ x) -f(x); 2) stworzyć relację

3) liczenie X stałe i  X0, znajdujemy
, które oznaczamy przez f” (x), jakby podkreślając, że wynikowa funkcja zależy tylko od wartości X, przy którym dochodzimy do limitu. Definicja: Pochodna y " =f " (x) dana funkcja y=f(x) dla danego x nazywa się granicą stosunku przyrostu funkcji do przyrostu argumentu, pod warunkiem, że przyrost argumentu dąży do zera, jeśli oczywiście ta granica istnieje, tj. skończone.
Zatem,

, Lub X Zauważ, że jeśli dla jakiejś wartości , na przykład kiedy x=a
, postawa  X Na k(x)0 nie dąży do granicy skończonej, wówczas w tym przypadku mówi się, że funkcja , na przykład kiedy Na , na przykład kiedy(lub w punkcie , na przykład kiedy.

) nie ma pochodnej lub nie jest różniczkowalna w punkcie

2. Znaczenie geometryczne pochodnej.

k(x)

Rozważmy wykres funkcji y = f (x), różniczkowalnej w pobliżu punktu x 0

Rozważmy dowolną prostą przechodzącą przez punkt na wykresie funkcji - punkt A(x 0, f (x 0)) i przecinającą wykres w pewnym punkcie B(x;f(x)). Taka prosta (AB) nazywana jest sieczną. Z ∆ABC: ​​​​AC = ∆x; BC = ∆у; tgβ=∆y/∆x.

Od AC || Wół, następnie ALO = BAC = β (odpowiednio dla równoległości). Ale ALO jest kątem nachylenia siecznej AB do dodatniego kierunku osi Wół. Oznacza to, że tanβ = k jest nachyleniem prostej AB.

Teraz zmniejszymy ∆х, tj. ∆х → 0. W tym przypadku punkt B zbliży się do punktu A zgodnie z wykresem, a sieczna AB będzie się obracać. Położeniem granicznym siecznej AB w punkcie ∆x → 0 będzie prosta (a), zwana styczną do wykresu funkcji y = f (x) w punkcie A.
Jeśli dojdziemy do granicy jako ∆x → 0 w równości tgβ =∆y/∆x, otrzymamy
ortg =f "(x 0), ponieważ
-kąt nachylenia stycznej do dodatniego kierunku osi Ox

z definicji pochodnej. Ale tg = k jest współczynnikiem kątowym stycznej, co oznacza k = tg = f „(x 0).

Zatem geometryczne znaczenie pochodnej jest następujące: 0 Pochodna funkcji w punkcie x 0 .

równe nachyleniu stycznej do wykresu funkcji narysowanej w punkcie z odciętą x

3. Znaczenie fizyczne pochodnej.

Rozważmy ruch punktu po linii prostej. Niech będzie podana współrzędna punktu w dowolnym momencie x(t). Wiadomo (z zajęć z fizyki), że średnia prędkość w pewnym okresie czasu jest równa stosunkowi drogi przebytej w tym okresie do czasu, czyli tj.

Vav = ∆x/∆t. Przejdźmy do granicy w ostatniej równości jako ∆t → 0.

lim Vav (t) = (t 0) - prędkość chwilowa w chwili t 0, ∆t → 0.

oraz lim = ∆x/∆t = x”(t 0) (z definicji pochodnej).

Zatem (t) =x"(t).Znaczenie fizyczne pochodnej jest następujące: pochodna funkcji = y(XFX 0 ) W punkcieyjest szybkością zmian funkcjiX 0

(x) w punkcie

Pochodną wykorzystuje się w fizyce do obliczania prędkości ze znanej funkcji współrzędnych w funkcji czasu oraz przyspieszenia ze znanej funkcji prędkości w funkcji czasu.

a(f) = "(t) - przyspieszenie, lub

Jeśli znane jest prawo ruchu punktu materialnego na okręgu, to można wyznaczyć prędkość kątową i przyspieszenie kątowe podczas ruchu obrotowego:

φ = φ(t) - zmiana kąta w czasie,

ω = φ"(t) - prędkość kątowa,

ε = φ"(t) - przyspieszenie kątowe, czyli ε = φ"(t).

Jeśli znane jest prawo rozkładu masy niejednorodnego pręta, można znaleźć gęstość liniową niejednorodnego pręta:

m = m(x) - masa,

x  , l - długość pręta,

p = m"(x) - gęstość liniowa.

Stosując pochodną rozwiązuje się problemy z teorii sprężystości i drgań harmonicznych. Zatem zgodnie z prawem Hooke’a

F = -kx, x – współrzędna zmienna, k – współczynnik sprężystości sprężyny. Zakładając ω 2 = k/m, otrzymujemy równanie różniczkowe wahadła sprężystego x”(t) + ω 2 x(t) = 0,

gdzie ω = √k/√m częstotliwość oscylacji (l/c), k - sztywność sprężyny (H/m).

Równanie w postaci y" + ω 2 y = 0 nazywane jest równaniem oscylacji harmonicznych (mechanicznych, elektrycznych, elektromagnetycznych). Rozwiązaniem takich równań jest funkcja

y = Asin(ωt + φ 0) lub y = Acos(ωt + φ 0), gdzie

A – amplituda oscylacji, ω – częstotliwość cykliczna,

φ 0 - faza początkowa.

Lekcja na temat: „Co to jest pochodna? Definicja pochodnej”

Dodatkowe materiały
Drodzy użytkownicy, nie zapomnijcie zostawić swoich komentarzy, recenzji i życzeń! Wszystkie materiały zostały sprawdzone programem antywirusowym.

Pomoce dydaktyczne i symulatory w sklepie internetowym Integral dla klasy 10
Zadania algebraiczne z parametrami, klasy 9–11
Środowisko oprogramowania „1C: Konstruktor matematyczny 6.1”

Co będziemy studiować:
1. Wprowadzenie do pojęcia pochodnej.
2. Trochę historii.

4. Pochodna na wykresie funkcji. Geometryczne znaczenie pochodnej.

6. Różniczkowanie funkcji.
7. Przykłady.

Wprowadzenie do pojęcia pochodnej

Istnieje wiele problemów, które mają zupełnie inne znaczenie, ale istnieją modele matematyczne, które pozwalają nam obliczyć rozwiązania naszych problemów w dokładnie ten sam sposób. Przykładowo, jeśli weźmiemy pod uwagę zadania takie jak:

A) Jest konto bankowe, które zmienia się co kilka dni, kwota stale rośnie, trzeba sprawdzić, z jaką szybkością rośnie konto.
b) Fabryka produkuje cukierki. Produkcja cukierków stale rośnie. Oblicz, jak szybko wzrasta wzrost ilości cukierków.
c) Prędkość samochodu w pewnym momencie t, jeżeli znane jest położenie samochodu i porusza się on po linii prostej.
d) Mamy wykres funkcji i w pewnym momencie rysujemy do niego styczną; musimy znaleźć tangens kąta nachylenia do stycznej.
Formułowanie naszych problemów jest zupełnie inne i wydaje się, że rozwiązuje się je na zupełnie inne sposoby, ale matematycy wymyślili, jak rozwiązać wszystkie te problemy dokładnie w ten sam sposób. Wprowadzono pojęcie pochodnej.

Trochę historii

Termin pochodna został wprowadzony przez wielkiego matematyka Lagrange'a, tłumaczenie na język rosyjski pochodzi od francuskiego słowa pochodna, a także wprowadził współczesną notację pochodnej, którą rozważymy później.
Leibniz i Newton rozważali w swoich pracach pojęcie pochodnej; znaleźli zastosowanie naszego terminu odpowiednio w geometrii i mechanice.
Nieco później dowiemy się, że pochodną wyznacza się przez granicę, ale w historii matematyki istnieje mały paradoks. Matematycy nauczyli się obliczać pochodną, ​​zanim wprowadzili pojęcie granicy i właściwie zrozumieli, czym jest pochodna.

Niech będzie zdefiniowana funkcja y=f(x) na pewnym przedziale zawierającym pewien punkt x0. Przyrost argumentu Δx nie opuszcza naszego przedziału. Znajdźmy przyrost Δy i ułóżmy stosunek Δy/Δx; jeśli istnieje granica tego stosunku, gdy Δx dąży do zera, to granicę tę nazywamy pochodną funkcji y=f(x) w punkcie x0 i oznaczamy f'(x0).

Spróbujmy wyjaśnić, czym jest pochodna w języku niematematycznym:
W języku matematycznym: pochodna to granica stosunku przyrostu funkcji do przyrostu jej argumentu, gdy przyrost argumentu dąży do zera.
W języku potocznym: pochodna to szybkość zmiany funkcji w punkcie x0.
Przyjrzyjmy się wykresom trzech funkcji:

Chłopaki, jak myślicie, która krzywa rośnie szybciej?
Odpowiedź wydaje się oczywista dla wszystkich: jedna krzywa rośnie szybciej niż pozostałe. Patrzymy, jak stromo rośnie wykres funkcji. Innymi słowy, jak szybko zmienia się współrzędna, gdy zmienia się x. Ta sama funkcja w różnych punktach może mieć różne wartości pochodnych – czyli może zmieniać się szybciej lub wolniej.

Pochodna na wykresie funkcji. Geometryczne znaczenie pochodnej

Zobaczmy teraz, jak znaleźć pochodną za pomocą wykresów funkcji:


Spójrzmy na nasz wykres funkcji: Narysujmy styczną do wykresu funkcji w punkcie z odciętą x0. Styczna i wykres naszej funkcji stykają się w punkcie A. Musimy oszacować, jak stromo rośnie wykres funkcji. Wygodną wartością jest tu tangens kąta stycznego.

Definicja. Pochodna funkcji w punkcie x0 jest równa tangensowi kąta stycznego narysowanego do wykresu funkcji w tym punkcie.

Kąt stycznej wybiera się jako kąt pomiędzy styczną a dodatnim kierunkiem osi x.
I tak pochodna naszej funkcji jest równa:

I tak pochodna w punkcie x0 jest równa tangensowi kąta stycznego, to jest geometryczne znaczenie pochodnej.

Algorytm wyznaczania pochodnej funkcji y=f(x).
a) Ustal wartość x, znajdź f(x).
b) Znajdź przyrost argumentu x+ Δx i wartość przyrostu funkcji f(x+ Δx).
c) Znajdź przyrost funkcji Δy= f(x+ Δx)-f(x).
d) Uzupełnij stosunek: Δy/Δx
e) Oblicz

To jest pochodna naszej funkcji.

Różniczkowanie funkcji

Jeżeli funkcja y=f(x) ma pochodną w punkcie x, to nazywa się ją różniczkowalną w punkcie x. Proces znajdowania pochodnej nazywamy różniczkowaniem funkcji y=f(x).
Wróćmy do zagadnienia ciągłości funkcji. Jeżeli funkcja jest różniczkowalna w pewnym punkcie, to można w tym punkcie narysować styczną do wykresu funkcji; funkcja nie może mieć w tym punkcie nieciągłości, wówczas po prostu nie można narysować stycznej.
Zapisujemy więc powyższe jako definicję:
Definicja. Jeżeli funkcja jest różniczkowalna w punkcie x, to jest w tym punkcie ciągła.
Jeżeli jednak funkcja jest w pewnym punkcie ciągła, nie oznacza to, że jest w tym punkcie różniczkowalna. Na przykład funkcja y=|x| w punkcie x=0 jest ciągła, ale nie można narysować stycznej, co oznacza, że ​​pochodna nie istnieje.

Przykłady pochodnych

Znajdź pochodną funkcji: y=3x
Rozwiązanie:
Będziemy korzystać z algorytmu wyszukiwania pochodnych.
1) Dla stałej wartości x wartość funkcji y=3x
2) W punkcie x+ Δx, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) Znajdź przyrost funkcji: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δ

Pochodna jest najważniejszym pojęciem w analizie matematycznej. Charakteryzuje zmianę funkcji argumentu X w pewnym momencie. Co więcej, sama pochodna jest funkcją argumentu X

Pochodna funkcji w punkcie jest granicą (jeśli istnieje i jest skończona) stosunku przyrostu funkcji do przyrostu argumentu, pod warunkiem, że ten ostatni dąży do zera.

Najczęściej używane są następujące notacja pochodna :

Przykład 1. Wykorzystując definicja pochodnej, znajdź pochodną funkcji

Rozwiązanie. Z definicji instrumentu pochodnego wynika następujący schemat jego obliczania.

Nadajmy argumentowi przyrost (delta) i znajdźmy przyrost funkcji:

Znajdźmy stosunek przyrostu funkcji do przyrostu argumentu:

Obliczmy granicę tego stosunku pod warunkiem, że przyrost argumentu dąży do zera, czyli do pochodnej wymaganej w stwierdzeniu problemu:

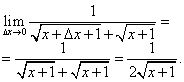
Fizyczne znaczenie pochodnej

DO pojęcie pochodnej doprowadziło do badań Galileo Galilei nad prawem swobodnego spadania ciał, a w szerszym znaczeniu - problemem chwilowej prędkości niejednostajnego ruchu prostoliniowego punktu.

Niech kamyk zostanie podniesiony, a następnie uwolniony z miejsca spoczynku. Ścieżka S przeniósł się w czasie T, jest funkcją czasu, tj. s = s(T). Jeśli podane jest prawo ruchu punktu, można wyznaczyć średnią prędkość w dowolnym okresie czasu. Niech w danym momencie kamyk będzie na swoim miejscu A, a w tej chwili - na stanowisku B. Przez pewien czas (od T do) punkt przekroczył ścieżkę. Zatem średnia prędkość ruchu w tym okresie czasu, którą oznaczamy przez , wynosi

.

Natomiast ruch swobodnie opadającego ciała jest wyraźnie nierówny. Prędkość w spadek stale rośnie. A średnia prędkość nie wystarcza już do scharakteryzowania prędkości poruszania się na różnych odcinkach trasy. Im krótszy okres czasu, tym dokładniejsza jest ta charakterystyka. W związku z tym wprowadza się pojęcie: chwilowa prędkość ruchu prostoliniowego (lub prędkość w danym momencie T) nazywa się średnią prędkością dozwoloną przy:

(pod warunkiem, że granica ta istnieje i jest skończona).

Okazuje się więc, że prędkość chwilowa jest granicą stosunku przyrostu funkcji S(T) do przyrostu argumentu T w Jest to pochodna, która w ogólnej formie jest zapisana w następujący sposób:.

.

Rozwiązaniem wskazanego problemu jest fizyczne znaczenie pochodnej . Zatem pochodna funkcji y=f(X) W punkcie X nazywa się granicą (jeśli istnieje i jest skończona) przyrostu funkcji do przyrostu argumentu, pod warunkiem, że ten ostatni dąży do zera.

Przykład 2. Znajdź pochodną funkcji

Rozwiązanie. Z definicji instrumentu pochodnego wynika następujący schemat jego obliczania.

Krok 1. Zwiększmy argument i znajdźmy

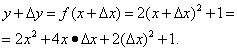
Krok 2. Znajdź przyrost funkcji:

Krok 3. Znajdź stosunek przyrostu funkcji do przyrostu argumentu:

Krok 4. Oblicz granicę tego stosunku przy , czyli pochodną:

Geometryczne znaczenie pochodnej

Niech funkcja będzie zdefiniowana na przedziale i niech będzie punkt M na wykresie funkcji odpowiada wartości argumentu i punktowi R- oznaczający. Przeciągnijmy przez punkty M I R linię prostą i zadzwoń sieczna. Oznaczmy przez kąt między sieczną a osią. Oczywiście kąt ten zależy od .

Jeśli istnieje

przejście przez ten punkt nazywa się pozycją graniczną siecznej PAN w (lub w ).

Styczna do wykresu funkcji w punkcie M zwane położeniem krańcowym siecznej PAN w , lub, co jest tym samym w .

Z definicji wynika, że ​​do istnienia stycznej wystarczy, że istnieje granica

,

a granica jest równa kątowi nachylenia stycznej do osi.

Podajmy teraz dokładną definicję stycznej.

Tangens do wykresu funkcji w punkcie prowadzi prosta przechodząca przez ten punkt i posiadająca nachylenie, tj. prosta, której równanie

Z tej definicji wynika, że pochodna funkcji jest równe nachyleniu stycznej do wykresu tej funkcji w punkcie z odciętą X. To jest geometryczne znaczenie pochodnej.

Zadanie B9 daje wykres funkcji lub pochodnej, z której należy wyznaczyć jedną z następujących wielkości:

1. Wartość pochodnej w pewnym punkcie x 0,
2. Punkty maksymalne lub minimalne (punkty ekstremalne),
3. Przedziały funkcji rosnących i malejących (przedziały monotoniczności).

Funkcje i pochodne przedstawione w tym zadaniu są zawsze ciągłe, co znacznie ułatwia rozwiązanie. Pomimo tego, że zadanie należy do sekcji analizy matematycznej, poradzą sobie z nim nawet najsłabsi uczniowie, gdyż nie jest tu wymagana głęboka wiedza teoretyczna.

Aby znaleźć wartość pochodnej, punkty ekstremalne i przedziały monotoniczności, istnieją proste i uniwersalne algorytmy - wszystkie zostaną omówione poniżej.

Przeczytaj uważnie warunki zadania B9, aby uniknąć głupich błędów: czasami trafiasz na dość długie teksty, ale jest kilka ważnych warunków, które wpływają na przebieg rozwiązania.

Obliczanie wartości pochodnej. Metoda dwupunktowa

Jeżeli zadaniu dany jest wykres funkcji f(x), stycznej do tego wykresu w pewnym punkcie x 0, i konieczne jest znalezienie w tym punkcie wartości pochodnej, stosuje się następujący algorytm:

1. Znajdź dwa „odpowiednie” punkty na wykresie stycznym: ich współrzędne muszą być liczbami całkowitymi. Oznaczmy te punkty jako A (x 1 ; y 1) i B (x 2 ; y 2). Zapisz poprawnie współrzędne - jest to kluczowy punkt rozwiązania, a każdy błąd tutaj doprowadzi do nieprawidłowej odpowiedzi.
2. Znając współrzędne łatwo obliczyć przyrost argumentu Δx = x 2 − x 1 oraz przyrost funkcji Δy = y 2 − y 1 .
3. Na koniec znajdujemy wartość pochodnej D = Δy/Δx. Innymi słowy, musisz podzielić przyrost funkcji przez przyrost argumentu - i to będzie odpowiedź.

Jeszcze raz zauważmy: punktów A i B należy szukać właśnie na stycznej, a nie jak to często bywa na wykresie funkcji f(x). Linia styczna będzie koniecznie zawierać co najmniej dwa takie punkty - w przeciwnym razie problem nie zostanie poprawnie sformułowany.

Rozważ punkty A (-3; 2) i B (-1; 6) i znajdź przyrosty:
Δx = x 2 - x 1 = -1 - (-3) = 2; Δy = y 2 - y 1 = 6 - 2 = 4.

Znajdźmy wartość pochodnej: D = Δy/Δx = 4/2 = 2.

Zadanie. Rysunek przedstawia wykres funkcji y = f(x) i styczną do niej w punkcie o odciętej x 0. Znajdź wartość pochodnej funkcji f(x) w punkcie x 0 .

Rozważ punkty A (0; 3) i B (3; 0), znajdź przyrosty:
Δx = x 2 - x 1 = 3 - 0 = 3; Δy = y 2 - y 1 = 0 - 3 = -3.

Teraz znajdujemy wartość pochodnej: D = Δy/Δx = −3/3 = −1.

Zadanie. Rysunek przedstawia wykres funkcji y = f(x) i styczną do niej w punkcie o odciętej x 0. Znajdź wartość pochodnej funkcji f(x) w punkcie x 0 .

Rozważ punkty A (0; 2) i B (5; 2) i znajdź przyrosty:
Δx = x 2 - x 1 = 5 - 0 = 5; Δy = y 2 - y 1 = 2 - 2 = 0.

Pozostaje znaleźć wartość pochodnej: D = Δy/Δx = 0/5 = 0.

Z ostatniego przykładu możemy sformułować regułę: jeżeli styczna jest równoległa do osi OX, to pochodna funkcji w punkcie styczności wynosi zero. W tym przypadku nie trzeba nawet niczego liczyć – wystarczy spojrzeć na wykres.

Obliczanie punktów maksymalnych i minimalnych

Czasami zamiast wykresu funkcji Zadanie B9 podaje wykres pochodnej i wymaga znalezienia punktu maksymalnego lub minimalnego funkcji. W tej sytuacji metoda dwupunktowa jest bezużyteczna, ale istnieje inny, jeszcze prostszy algorytm. Najpierw zdefiniujmy terminologię:

1. Punkt x 0 nazywany jest punktem maksymalnym funkcji f(x), jeśli w jakimś sąsiedztwie tego punktu zachodzi nierówność: f(x 0) ≥ f(x).
2. Punkt x 0 nazywany jest punktem minimalnym funkcji f(x), jeżeli w jakimś sąsiedztwie tego punktu zachodzi nierówność: f(x 0) ≤ f(x).

Aby znaleźć maksimum i minimum punktów z wykresu pochodnej, wykonaj następujące kroki:

1. Narysuj ponownie wykres pochodnej, usuwając wszystkie niepotrzebne informacje. Jak pokazuje praktyka, niepotrzebne dane jedynie zakłócają decyzję. Dlatego zaznaczamy zera pochodnej na osi współrzędnych - i tyle.
2. Znajdź znaki pochodnej na przedziałach między zerami. Jeżeli dla jakiegoś punktu x 0 wiadomo, że f'(x 0) ≠ 0, to możliwe są tylko dwie opcje: f'(x 0) ≥ 0 lub f'(x 0) ≤ 0. Znak pochodnej wynosi łatwo wyznaczyć z oryginalnego rysunku: jeśli wykres pochodnej leży powyżej osi OX, to f'(x) ≥ 0. I odwrotnie, jeśli wykres pochodnej leży poniżej osi OX, to f'(x) ≤ 0.
3. Ponownie sprawdzamy zera i znaki pochodnej. Tam, gdzie znak zmienia się z minus na plus, jest to punkt minimalny. I odwrotnie, jeśli znak pochodnej zmienia się z plusa na minus, jest to punkt maksymalny. Liczenie odbywa się zawsze od lewej do prawej.

Ten schemat działa tylko dla funkcji ciągłych - w zadaniu B9 nie ma innych.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na przedziale [−5; 5]. Znajdź punkt minimalny funkcji f(x) na tym odcinku.

Pozbądźmy się niepotrzebnych informacji i zostawmy jedynie granice [−5; 5] i zera pochodnej x = −3 i x = 2,5. Zwracamy również uwagę na znaki:

Oczywiście w punkcie x = −3 znak pochodnej zmienia się z minus na plus. To jest minimalny punkt.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na przedziale [−3; 7]. Znajdź maksymalny punkt funkcji f(x) na tym odcinku.

Narysujmy wykres na nowo, pozostawiając jedynie granice [−3; 7] oraz zera pochodnej x = −1,7 i x = 5. Zwróćmy uwagę na znaki pochodnej na otrzymanym wykresie. Mamy:

Oczywiście w punkcie x = 5 znak pochodnej zmienia się z plusa na minus - jest to punkt maksymalny.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x), określonej na przedziale [−6; 4]. Znajdź liczbę maksymalnych punktów funkcji f(x) należących do odcinka [−4; 3].

Z warunków zadania wynika, że ​​wystarczy uwzględnić tylko część grafu ograniczoną odcinkiem [−4; 3]. Dlatego budujemy nowy graf, na którym zaznaczamy jedynie granice [−4; 3] i zera znajdującej się w nim pochodnej. Mianowicie punkty x = −3,5 i x = 2. Otrzymujemy:

Na tym wykresie jest tylko jeden punkt maksymalny x = 2. To w tym momencie znak pochodnej zmienia się z plusa na minus.

Mała uwaga dotycząca punktów o współrzędnych niecałkowitych. Przykładowo w ostatnim zadaniu uwzględniono punkt x = −3,5, ale z takim samym sukcesem możemy przyjąć x = −3,4. Jeśli problem zostanie poprawnie skompilowany, takie zmiany nie powinny mieć wpływu na odpowiedź, ponieważ punkty „bez stałego miejsca zamieszkania” nie biorą bezpośredniego udziału w rozwiązaniu problemu. Oczywiście ta sztuczka nie będzie działać w przypadku punktów całkowitych.

Znajdowanie przedziałów funkcji rosnących i malejących

W takim problemie, podobnie jak punkty maksymalne i minimalne, proponuje się użycie wykresu pochodnej do znalezienia obszarów, w których sama funkcja rośnie lub maleje. Najpierw zdefiniujmy, czym jest wzrost i spadek:

1. Mówi się, że funkcja f(x) na odcinku jest rosnąca, jeśli dla dowolnych dwóch punktów x 1 i x 2 z tego odcinka prawdziwe jest stwierdzenie: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Innymi słowy, im większa wartość argumentu, tym większa wartość funkcji.
2. Mówi się, że funkcja f(x) na odcinku jest malejąca, jeżeli dla dowolnych dwóch punktów x 1 i x 2 z tego odcinka prawdziwe jest stwierdzenie: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Te. Większa wartość argumentu odpowiada mniejszej wartości funkcji.

Sformułujmy warunki wystarczające do zwiększania i zmniejszania:

1. Aby funkcja ciągła f(x) wzrosła na odcinku , wystarczy, że jej pochodna wewnątrz odcinka będzie dodatnia, tj. f’(x) ≥ 0.
2. Aby funkcja ciągła f(x) malała na odcinku , wystarczy, aby jej pochodna wewnątrz odcinka była ujemna, tj. f’(x) ≤ 0.

Przyjmijmy te twierdzenia bez dowodów. Otrzymujemy w ten sposób schemat znajdowania przedziałów rosnących i malejących, który pod wieloma względami jest podobny do algorytmu obliczania punktów ekstremalnych:

1. Usuń wszystkie niepotrzebne informacje. Na oryginalnym wykresie pochodnej interesują nas przede wszystkim zera funkcji, więc tylko je pozostawimy.
2. Zaznacz znaki pochodnej w odstępach między zerami. Gdzie f’(x) ≥ 0, funkcja rośnie, a gdzie f’(x) ≤ 0, maleje. Jeśli problem nakłada ograniczenia na zmienną x, dodatkowo zaznaczamy je na nowym wykresie.
3. Teraz, gdy znamy zachowanie funkcji i ograniczenia, pozostaje obliczyć wielkość wymaganą w zadaniu.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x) określonej na przedziale [−3; 7,5]. Znajdź przedziały zmniejszania się funkcji f(x). W swojej odpowiedzi podaj sumę liczb całkowitych zawartych w tych przedziałach.

Jak zwykle przerysujmy wykres i zaznaczmy granice [−3; 7,5], a także zera pochodnych x = −1,5 i x = 5,3. Następnie zauważamy znaki pochodnej. Mamy:

Ponieważ pochodna jest ujemna na przedziale (-1,5), jest to przedział funkcji malejącej. Pozostaje zsumować wszystkie liczby całkowite znajdujące się w tym przedziale:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Zadanie. Rysunek przedstawia wykres pochodnej funkcji f(x), określonej na przedziale [−10; 4]. Znajdź przedziały rosnącej funkcji f(x). W swojej odpowiedzi podaj długość największego z nich.

Pozbądźmy się niepotrzebnych informacji. Zostawmy tylko granice [−10; 4] i zera pochodnej, których tym razem było cztery: x = −8, x = −6, x = −3 i x = 2. Zaznaczmy znaki pochodnej i otrzymamy następujący obraz:

Interesują nas przedziały funkcji rosnącej, tj. np. gdzie f’(x) ≥ 0. Na wykresie występują dwa takie przedziały: (−8; −6) i (−3; 2). Obliczmy ich długości:
l 1 = - 6 - (-8) = 2;
l 2 = 2 - (-3) = 5.

Ponieważ musimy znaleźć długość największego z przedziałów, jako odpowiedź zapisujemy wartość l 2 = 5.