Vector product of a matrix. How to find the cross product of vectors

Dot product properties

Dot product of vectors, definition, properties

Linear operations on vectors.

Vectors, basic concepts, definitions, linear operations on them

A vector on a plane is an ordered pair of its points, while the first point is called the beginning, and the second the end - of the vector

Two vectors are called equal if they are equal and codirectional.

Vectors that lie on the same line are called codirectional if they are codirectional with some of the same vector that does not lie on this line.

Vectors that lie on the same line or on parallel lines are called collinear, and collinear but not codirectional are called oppositely directed.

Vectors lying on perpendicular lines are called orthogonal.

Definition 5.4. sum a+b vectors a And b is called the vector coming from the beginning of the vector A to the end of the vector b , if the beginning of the vector b coincides with the end of the vector A .

Definition 5.5. difference a - b vectors A And b such a vector is called With , which together with the vector b gives a vector A .

Definition 5.6. workk a vector A per number k called vector b , collinear vector A , which has module equal to | k||a |, and a direction that is the same as the direction A at k>0 and opposite A at k<0.

Properties of multiplication of a vector by a number:

Property 1. k(a+b ) = k a+ k b.

Property 2. (k+m)a = k a+ m a.

Property 3. k(m a) = (km)a .

Consequence. If non-zero vectors A And b are collinear, then there is a number k, What b= k a.

The scalar product of two nonzero vectors a And b called a number (scalar) equal to the product of the lengths of these vectors and the cosine of the angle φ between them. The scalar product can be expressed in various ways, for example, as ab, a · b, (a , b), (a · b). So the dot product is:

a · b = |a| · | b| cos φ

If at least one of the vectors is equal to zero, then the scalar product is equal to zero.

Permutation property: a · b = b · a(the scalar product does not change from permutation of factors);

distribution property: a · ( b · c) = (a · b) · c(the result does not depend on the order of multiplication);

Combination property (in relation to the scalar factor): (λ a) · b = λ ( a · b).

Property of orthogonality (perpendicularity): if the vector a And b non-zero, then their dot product is zero only when these vectors are orthogonal (perpendicular to each other) a ┴ b;

Square property: a · a = a 2 = |a| 2 (the scalar product of a vector with itself is equal to the square of its modulus);

If the coordinates of the vectors a=(x 1 , y 1 , z 1 ) and b=(x 2 , y 2 , z 2 ), then the scalar product is a · b= x 1 x 2 + y 1 y 2 + z 1 z 2 .

Vector holding vectors. Definition: The vector product of two vectors and is understood as a vector for which:

The module is equal to the area of ​​the parallelogram built on these vectors, i.e. , where is the angle between the vectors and

This vector is perpendicular to the multiplied vectors, i.e.

If the vectors are non-collinear, then they form a right triple of vectors.

Cross product properties:

1. When the order of the factors is changed, the vector product changes its sign to the opposite, preserving the module, i.e.

2 .Vector square is equal to zero-vector, i.e.

3 .The scalar factor can be taken out of the sign of the vector product, i.e.

4 .For any three vectors, the equality

5 .Necessary and sufficient condition for the collinearity of two vectors and :

This online calculator calculates the cross product of vectors. A detailed solution is given. To calculate the cross product of vectors, enter the coordinates of the vectors in the cells and click on the "Calculate."

×

Warning

Clear all cells?

Close Clear

Data entry instruction. Numbers are entered as whole numbers (examples: 487, 5, -7623, etc.), decimal numbers (eg. 67., 102.54, etc.) or fractions. The fraction must be typed in the form a/b, where a and b (b>0) are integer or decimal numbers. Examples 45/5, 6.6/76.4, -7/6.7, etc.

Cross product of vectors

Before proceeding to the definition of the vector product of vectors, consider the concepts ordered triple of vectors, left triple of vectors, right triple of vectors.

Definition 1. Three vectors are called ordered triple(or triple) if it is indicated which of these vectors is the first, which is the second and which is the third.

Recording cba- means - the first is a vector c, the second is the vector b and the third is the vector a.

Definition 2. A triple of non-coplanar vectors abc called right (left) if, when reduced to a common beginning, these vectors are located as the large, unbent index and middle fingers of the right (left) hand are respectively located.

Definition 2 can be formulated in another way.

Definition 2. A triple of non-coplanar vectors abc is called right (left) if, when reduced to a common origin, the vector c located on the other side of the plane defined by the vectors a And b, whence the shortest turn from a To b performed counterclockwise (clockwise).

Vector trio abc shown in fig. 1 is right and triple abc shown in fig. 2 is left.

If two triples of vectors are right or left, then they are said to have the same orientation. Otherwise, they are said to be of opposite orientation.

Definition 3. A Cartesian or affine coordinate system is called right (left) if the three basis vectors form a right (left) triple.

For definiteness, in what follows we will consider only right-handed coordinate systems.

Definition 4. vector art vector a per vector b called vector With, denoted by the symbol c=[ab] (or c=[a,b], or c=a×b) and satisfying the following three requirements:

• vector length With is equal to the product of the lengths of the vectors a And b to the sine of the angle φ between them:

|c|=|[ab]|=|a||b|sinφ;

(1)

• vector With orthogonal to each of the vectors a And b;
• vector c directed so that the three abc is right.

The cross product of vectors has the following properties:

• [ab]=−[ba] (antipermutability factors);
• [(λa)b]=λ [ab] (compatibility relative to the numerical factor);
• [(a+b)c]=[ac]+[bc] (distribution relative to the sum of vectors);
• [aa]=0 for any vector a.

Geometric properties of the cross product of vectors

Theorem 1. For two vectors to be collinear, it is necessary and sufficient that their vector product be equal to zero.

Proof. Necessity. Let the vectors a And b collinear. Then the angle between them is 0 or 180° and sinφ=sin180=sin 0=0. Therefore, taking into account expression (1), the length of the vector c equals zero. Then c null vector.

Adequacy. Let the cross product of vectors a And b nav to zero: [ ab]=0. Let us prove that the vectors a And b collinear. If at least one of the vectors a And b zero, then these vectors are collinear (because the zero vector has an indefinite direction and can be considered collinear to any vector).

If both vectors a And b nonzero, then | a|>0, |b|>0. Then from [ ab]=0 and from (1) it follows that sinφ=0. Hence the vectors a And b collinear.

The theorem has been proven.

Theorem 2. The length (modulus) of the vector product [ ab] equals the area S parallelogram built on vectors reduced to a common origin a And b.

Proof. As you know, the area of ​​a parallelogram is equal to the product of the adjacent sides of this parallelogram and the sine of the angle between them. Hence:

Then the cross product of these vectors has the form:

Expanding the determinant over the elements of the first row, we get the decomposition of the vector a×b basis i, j, k, which is equivalent to formula (3).

Proof of Theorem 3. Compose all possible pairs of basis vectors i, j, k and calculate their vector product. It should be taken into account that the basis vectors are mutually orthogonal, form a right triple, and have unit length (in other words, we can assume that i={1, 0, 0}, j={0, 1, 0}, k=(0, 0, 1)). Then we have:

From the last equality and relations (4), we obtain:

Compose a 3×3 matrix, the first row of which are the basis vectors i, j, k, and the remaining rows are filled with elements of vectors a And b:

Thus, the result of the cross product of vectors a And b will be a vector:

.

Example 2. Find the cross product of vectors [ ab], where the vector a represented by two dots. Starting point of vector a: , the end point of the vector a: , vector b has the form .

Solution. Move the first vector to the origin. To do this, subtract from the corresponding coordinates of the end point the coordinates of the start point:

We calculate the determinant of this matrix by expanding it in the first row. As a result of these calculations, we obtain the vector product of vectors a And b.

Definition. The vector product of a vector a and vector b is a vector denoted by the symbol [«, b] (or l x b), such that 1) the length of the vector [a, b] is equal to (p, where y is the angle between the vectors a and b ( 31); 2) the vector [a, b) is perpendicular to the vectors a and b, i.e. perpendicular to the plane of these vectors; 3) the vector [a, b] is directed in such a way that from the end of this vector the shortest turn from a to b is seen to occur counterclockwise (Fig. 32). Rice. 32 Fig.31 In other words, the vectors a, b and [а, b) form the right triple of vectors, i.e. located like the thumb, index and middle fingers of the right hand. If the vectors a and b are collinear, we will assume that [a, b] = 0. By definition, the length of the vector product is numerically equal to the area Sa of the parallelogram (Fig. 33) built on the multiplied vectors a and b as on the sides: 6.1 . Properties of a vector product 1. A vector product is equal to a zero vector if and only if at least one of the multiplied vectors is zero or when these vectors are collinear (if the vectors a and b are collinear, then the angle between them is either 0 or 7r). This is easy to obtain from the fact that If we consider the zero vector collinsar to any vector, then the condition for the collinarity of the vectors a and b can be expressed as follows 2. The vector product is anticommutative, i.e. always. Indeed, the vectors (a, b) and have the same length and are collinear. The directions of these vectors are opposite, since from the end of the vector [a, b] the shortest turn from a to b will be seen occurring counterclockwise, and from the end of the vector [b, a] - clockwise (Fig. 34). 3. The vector product has a distributive property with respect to addition 4. The numerical factor A can be taken out of the sign of the vector product 6.2. Vector product of vectors given by coordinates Let the vectors a and b be given by their coordinates in the basis. Using the distribution property of the vector product, we find the vector product of the vectors given by the coordinates. Mixed work. Let us write out the vector products of coordinate orts (Fig. 35): Therefore, for the vector product of vectors a and b, we obtain from formula (3) the following expression determinant over the elements of the 1st row, we obtain (4). Examples. 1. Find the area of ​​a parallelogram built on vectors Find the area of ​​the triangle (Fig. 36). It is clear that the area b "d of the triangle JSC is equal to half the area S of the parallelogram O AC B. Calculating the vector product (a, b | of the vectors a \u003d OA and b \u003d b \u003d ob), we obtain (a, b), c) = [a, |b, c)) is not true in the general case. For example, for a = ss j we have § 7. Mixed product of vectors Let we have three vectors a, b and c. Multiply the vectors a and 1> vectorially. As a result, we obtain the vector [a, 1>]. We multiply it scalarly by the vector c: (k b), c. The number ([a, b], e) is called the mixed product of the vectors a, b. c and is denoted by the symbol (a, 1), e). 7.1. The geometric meaning of the mixed product Let us set aside the vectors a, b and from the general point O (Fig. 37). If all four points O, A, B, C lie in the same plane ( vectors a, b and c are called in this case coplanar), then the mixed product ([a, b], c) = 0. This follows from the fact that the vector [a, b| is perpendicular to the plane in which the vectors a and 1 lie ”, and hence the vector c. / If the points O, A, B, C do not lie in the same plane (vectors a, b and c are non-coplanar), we will build a parallelepiped on the edges OA, OB and OS (Fig. 38 a). By the definition of the cross product, we have (a,b) = So c, where So is the area of ​​the parallelogram OADB, and c is a unit vector perpendicular to the vectors a and b and such that the triple a, b, c is right, i.e. vectors a, b and c are located respectively as the thumb, index and middle fingers of the right hand (Fig. 38 b). Multiplying both parts of the last equality on the right scalar by the vector c, we get that the vector product of the vectors given by the coordinates. Mixed work. The number rc c is equal to the height h of the constructed parallelepiped, taken with the “+” sign if the angle between the vectors c and c is acute (the triple a, b, c is right), and with the sign “-” if the angle is obtuse (the triple a, b, c - left), so that Thus, the mixed product of the vectors a, b and c is equal to the volume V of the parallelepiped built on these vectors as on edges if the triple a, b, c is right, and -V if the triple a , b, c - left. Based on the geometric meaning of the mixed product, we can conclude that by multiplying the same vectors a, b and c in any other order, we will always get either +7 or -K. The sign of pro- Fig. 38 reference will depend only on which triplet the multiplied vectors form - right or left. If the vectors a, b, c form a right triple, then the triples b, c, a and c, a, b will also be right. At the same time, all three triplets b, a, c; a, c, b and c, b, a - left. Thus, (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b ,A). We emphasize once again that the mixed product of vectors is equal to zero if and only if the multiplied vectors a, b, c are coplanar: (a, b, c are coplanar) 7.2. Mixed Product in Coordinates Let the vectors a, b, c be given by their coordinates in the basis i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Let us find an expression for their mixed product (a, b, c). We have a mixed product of vectors given by their coordinates in the basis i, J, k, equal to the third-order determinant, the lines of which are composed, respectively, of the coordinates of the first, second and third of the multiplied vectors. The necessary and sufficient condition for the complanarity of the vectors a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) can be written in the following form z, ar2 y2 -2 =0. Uz Example. Check whether the vectors v = (7,4,6), b = (2, 1,1), c = (19, II, 17) are coplanar. The vectors under consideration will be coplanar or non-coplanar, depending on whether the determinant is equal to zero or not. Expanding it in terms of the elements of the first row, we obtain 7.3. Double cross product The double cross product [a, [b, c]] is a vector perpendicular to the vectors a and [b, c]. Therefore, it lies in the plane of the vectors b and c and can be expanded in these vectors. It can be shown that the formula [a, [!>, c]] = b(a, e) - c(a, b) is valid. Exercises 1. Three vectors AB = c, W? = o and CA = b serve as sides of the triangle. Express in terms of a, b and c the vectors coinciding with the medians AM, DN, CP of the triangle. 2. What condition must be connected between the vectors p and q so that the vector p + q divides the angle between them in half? It is assumed that all three vectors are related to a common origin. 3. Calculate the length of the diagonals of the parallelogram built on the vectors a = 5p + 2q and b = p - 3q, if it is known that |p| = 2v/2, |q| = 3 H-(p7ci) = f. 4. Denoting by a and b the sides of the rhombus emerging from a common vertex, prove that the diagonals of the rhombus are mutually perpendicular. 5. Calculate the dot product of the vectors a = 4i + 7j + 3k and b = 31 - 5j + k. 6. Find the unit vector a0 parallel to the vector a = (6, 7, -6). 7. Find the projection of the vector a = l+ j- kHa vector b = 21 - j - 3k. 8. Find the cosine of the angle between the vectors IS "w, if A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Find a unit vector p° that is simultaneously perpendicular to the vector a = (3, 6, 8) and the x-axis. 10. Calculate the sine of the angle between the diagonals of the parallelopham built on the vectors a = 2i+J-k, b=i-3j + k as on the sides. Calculate the height h of the parallelepiped built on the vectors a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k, if the parallelogram built on the vectors a and I is taken as the base). Answers

Obviously, in the case of a cross product, the order in which the vectors are taken matters, moreover,

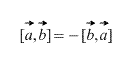
Also, directly from the definition it follows that for any scalar factor k (number) the following is true:

The cross product of collinear vectors is equal to the zero vector. Moreover, the cross product of two vectors is zero if and only if they are collinear. (In case one of them is a zero vector it is necessary to remember that the zero vector is collinear to any vector by definition).

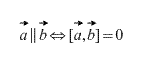
Vector product has distributive property, that is

The expression of the cross product in terms of the coordinates of the vectors.

Let two vectors be given

(how to find the coordinates of a vector by the coordinates of its beginning and end - see the article Dot product of vectors, paragraph Alternative definition of the dot product, or calculating the dot product of two vectors given by their coordinates.)

Why do you need a vector product?

There are many ways to use the cross product, for example, as already written above, by calculating the cross product of two vectors, you can find out if they are collinear.

Or it can be used as a way to calculate the area of ​​a parallelogram built from these vectors. Based on the definition, the length of the resulting vector is the area of ​​this parallelogram.

Online calculator of vector product.

To find the scalar product of two vectors using this calculator, you need to enter the coordinates of the first vector in the first line in order, and the second vector in the second. The coordinates of vectors can be calculated from their start and end coordinates (see article Dot product of vectors , item An alternative definition of the dot product, or calculating the dot product of two vectors given their coordinates.)

Definition. The vector product of a vector a (multiplier) by a vector (multiplier) that is not collinear to it is the third vector c (product), which is constructed as follows:

1) its modulus is numerically equal to the area of ​​the parallelogram in fig. 155), built on vectors, i.e., it is equal to the direction perpendicular to the plane of the mentioned parallelogram;

3) in this case, the direction of the vector c is chosen (out of two possible ones) so that the vectors c form a right-handed system (§ 110).

Designation: or

Addendum to the definition. If the vectors are collinear, then considering the figure as a (conditionally) parallelogram, it is natural to assign zero area. Therefore, the vector product of collinear vectors is considered equal to the null vector.

Since the null vector can be assigned any direction, this convention does not contradict items 2 and 3 of the definition.

Remark 1. In the term "vector product", the first word indicates that the result of an action is a vector (as opposed to a scalar product; cf. § 104, remark 1).

Example 1. Find the vector product where the main vectors of the right coordinate system (Fig. 156).

1. Since the lengths of the main vectors are equal to the scale unit, the area of ​​the parallelogram (square) is numerically equal to one. Hence, the modulus of the vector product is equal to one.

2. Since the perpendicular to the plane is the axis, the desired vector product is a vector collinear to the vector k; and since both of them have modulus 1, the required cross product is either k or -k.

3. Of these two possible vectors, the first must be chosen, since the vectors k form a right system (and the vectors form a left one).

Example 2. Find the cross product

Solution. As in example 1, we conclude that the vector is either k or -k. But now we need to choose -k, since the vectors form the right system (and the vectors form the left). So,

Example 3 The vectors have lengths of 80 and 50 cm, respectively, and form an angle of 30°. Taking a meter as a unit of length, find the length of the vector product a

Solution. The area of ​​a parallelogram built on vectors is equal to The length of the desired vector product is equal to

Example 4. Find the length of the cross product of the same vectors, taking a centimeter as a unit of length.

Solution. Since the area of ​​the parallelogram built on vectors is equal to the length of the vector product is 2000 cm, i.e.

Comparison of examples 3 and 4 shows that the length of the vector depends not only on the lengths of the factors, but also on the choice of the length unit.

The physical meaning of the vector product. Of the many physical quantities represented by the vector product, we will consider only the moment of force.

Let A be the point of application of the force. The moment of force relative to the point O is called the vector product. Since the module of this vector product is numerically equal to the area of ​​the parallelogram (Fig. 157), the module of the moment is equal to the product of the base by the height, i.e., the force multiplied by the distance from the point O to the straight line along which the force acts.

In mechanics, it is proved that for the equilibrium of a rigid body it is necessary that not only the sum of the vectors representing the forces applied to the body, but also the sum of the moments of forces should be equal to zero. In the case when all forces are parallel to the same plane, the addition of the vectors representing the moments can be replaced by the addition and subtraction of their moduli. But for arbitrary directions of forces, such a replacement is impossible. In accordance with this, the cross product is defined precisely as a vector, and not as a number.