Division e. Division of an extraordinary fraction by a natural number

Lesson content

Adding fractions with the same denominators

Adding fractions is of two types:

1. Adding fractions with the same denominators
2. Adding fractions with different denominators

Let's start with adding fractions with the same denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators, and leave the denominator unchanged. For example, let's add the fractions and . We add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2 Add fractions and .

The answer is an improper fraction. If the end of the task comes, then it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part in it. In our case, the integer part is allocated easily - two divided by two is equal to one:

This example can be easily understood if we think of a pizza that is divided into two parts. If you add more pizzas to the pizza, you get one whole pizza:

Example 3. Add fractions and .

Again, add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you add more pizzas to pizza, you get pizzas:

Example 4 Find the value of an expression

This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:

Let's try to depict our solution using a picture. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, adding fractions with the same denominators is not difficult. It is enough to understand the following rules:

1. To add fractions with the same denominator, you need to add their numerators, and leave the denominator unchanged;

Adding fractions with different denominators

Now we will learn how to add fractions with different denominators. When adding fractions, the denominators of those fractions must be the same. But they are not always the same.

For example, fractions can be added because they have the same denominators.

But fractions cannot be added at once, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

There are several ways to reduce fractions to the same denominator. Today we will consider only one of them, since the rest of the methods may seem complicated for a beginner.

The essence of this method lies in the fact that first (LCM) of the denominators of both fractions is sought. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained. They do the same with the second fraction - the LCM is divided by the denominator of the second fraction and the second additional factor is obtained.

Then the numerators and denominators of the fractions are multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.

Example 1. Add fractions and

First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6

LCM (2 and 3) = 6

Now back to fractions and . First, we divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.

The resulting number 2 is the first additional factor. We write it down to the first fraction. To do this, we make a small oblique line above the fraction and write down the found additional factor above it:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.

The resulting number 3 is the second additional factor. We write it to the second fraction. Again, we make a small oblique line above the second fraction and write the found additional factor above it:

Now we are all set to add. It remains to multiply the numerators and denominators of fractions by their additional factors:

Look closely at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's complete this example to the end:

Thus the example ends. To add it turns out.

Let's try to depict our solution using a picture. If you add pizzas to a pizza, you get one whole pizza and another sixth of a pizza:

Reduction of fractions to the same (common) denominator can also be depicted using a picture. Bringing the fractions and to a common denominator, we get the fractions and . These two fractions will be represented by the same slices of pizzas. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing shows a fraction (four pieces out of six) and the second picture shows a fraction (three pieces out of six). Putting these pieces together we get (seven pieces out of six). This fraction is incorrect, so we have highlighted the integer part in it. The result was (one whole pizza and another sixth pizza).

Note that we have painted this example in too much detail. In educational institutions it is not customary to write in such a detailed manner. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the additional factors found by your numerators and denominators. While at school, we would have to write this example as follows:

But there is also the other side of the coin. If detailed notes are not made at the first stages of studying mathematics, then questions of the kind “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.

To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:

1. Find the LCM of the denominators of fractions;
2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction;
3. Multiply the numerators and denominators of fractions by their additional factors;
4. Add fractions that have the same denominators;
5. If the answer turned out to be an improper fraction, then select its whole part;

Example 2 Find the value of an expression .

Let's use the instructions above.

Step 1. Find the LCM of the denominators of fractions

Find the LCM of the denominators of both fractions. The denominators of the fractions are the numbers 2, 3 and 4

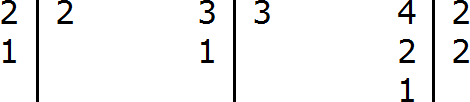
Step 2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction

Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it over the first fraction:

Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. Divide 12 by 3, we get 4. We got the second additional factor 4. We write it over the second fraction:

Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We got the third additional factor 3. We write it over the third fraction:

Step 3. Multiply the numerators and denominators of fractions by your additional factors

We multiply the numerators and denominators by our additional factors:

Step 4. Add fractions that have the same denominators

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. It remains to add these fractions. Add up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is carried over to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of a new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.

Step 5. If the answer turned out to be an improper fraction, then select the whole part in it

Our answer is an improper fraction. We must single out the whole part of it. We highlight:

Got an answer

Subtraction of fractions with the same denominators

There are two types of fraction subtraction:

1. Subtraction of fractions with the same denominators
2. Subtraction of fractions with different denominators

First, let's learn how to subtract fractions with the same denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same.

For example, let's find the value of the expression . To solve this example, it is necessary to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we think of a pizza that is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2 Find the value of the expression .

Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3 Find the value of an expression

This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction, you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated in subtracting fractions with the same denominators. It is enough to understand the following rules:

1. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
2. If the answer turned out to be an improper fraction, then you need to select the whole part in it.

Subtraction of fractions with different denominators

For example, a fraction can be subtracted from a fraction, since these fractions have the same denominators. But a fraction cannot be subtracted from a fraction, since these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

The common denominator is found according to the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written over the second fraction.

The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to subtract such fractions.

Example 1 Find the value of an expression:

These fractions have different denominators, so you need to bring them to the same (common) denominator.

First, we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12

LCM (3 and 4) = 12

Now back to fractions and

Let's find an additional factor for the first fraction. To do this, we divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. We write the four over the first fraction:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a triple over the second fraction:

Now we are all set for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's complete this example to the end:

Got an answer

Let's try to depict our solution using a picture. If you cut pizzas from a pizza, you get pizzas.

This is the detailed version of the solution. Being at school, we would have to solve this example in a shorter way. Such a solution would look like this:

Reduction of fractions and to a common denominator can also be depicted using a picture. Bringing these fractions to a common denominator, we get the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into the same fractions (reduced to the same denominator):

The first drawing shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting off three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.

Example 2 Find the value of an expression

These fractions have different denominators, so you first need to bring them to the same (common) denominator.

Find the LCM of the denominators of these fractions.

The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30

LCM(10, 3, 5) = 30

Now we find additional factors for each fraction. To do this, we divide the LCM by the denominator of each fraction.

Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it over the first fraction:

Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it over the second fraction:

Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it over the third fraction:

Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.

The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a correct fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it easier. What can be done? You can reduce this fraction.

To reduce a fraction, you need to divide its numerator and denominator by (gcd) the numbers 20 and 30.

So, we find the GCD of the numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found GCD, that is, by 10

Got an answer

Multiplying a fraction by a number

To multiply a fraction by a number, you need to multiply the numerator of the given fraction by this number, and leave the denominator the same.

Example 1. Multiply the fraction by the number 1.

Multiply the numerator of the fraction by the number 1

The entry can be understood as taking half 1 time. For example, if you take pizza 1 time, you get pizza

From the laws of multiplication, we know that if the multiplicand and the multiplier are interchanged, then the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying an integer and a fraction works:

This entry can be understood as taking half of the unit. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression

Multiply the numerator of the fraction by 4

The answer is an improper fraction. Let's take a whole part of it:

The expression can be understood as taking two quarters 4 times. For example, if you take pizzas 4 times, you get two whole pizzas.

And if we swap the multiplicand and the multiplier in places, we get the expression. It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

Multiplication of fractions

To multiply fractions, you need to multiply their numerators and denominators. If the answer is an improper fraction, you need to select the whole part in it.

Example 1 Find the value of the expression .

Got an answer. It is desirable to reduce this fraction. The fraction can be reduced by 2. Then the final solution will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:

How to take two-thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll get pizza. Remember what a pizza looks like divided into three parts:

One slice from this pizza and the two slices we took will have the same dimensions:

In other words, we are talking about the same pizza size. Therefore, the value of the expression is

Example 2. Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer is an improper fraction. Let's take a whole part of it:

Example 3 Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer turned out to be a correct fraction, but it will be good if it is reduced. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor (GCD) of the numbers 105 and 450.

So, let's find the GCD of the numbers 105 and 450:

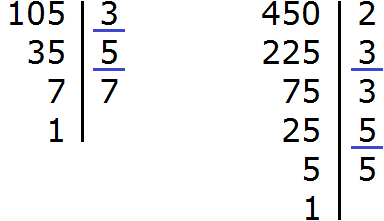
Now we divide the numerator and denominator of our answer to the GCD that we have now found, that is, by 15

Representing an integer as a fraction

Any whole number can be represented as a fraction. For example, the number 5 can be represented as . From this, the five will not change its meaning, since the expression means “the number five divided by one”, and this, as you know, is equal to five:

Reverse numbers

Now we will get acquainted with a very interesting topic in mathematics. It's called "reverse numbers".

Definition. Reverse to numbera is the number that, when multiplied bya gives a unit.

Let's substitute in this definition instead of a variable a number 5 and try to read the definition:

Reverse to number 5 is the number that, when multiplied by 5 gives a unit.

Is it possible to find a number that, when multiplied by 5, gives one? It turns out you can. Let's represent five as a fraction:

Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let's multiply the fraction by itself, only inverted:

What will be the result of this? If we continue to solve this example, we get one:

This means that the inverse of the number 5 is the number, since when 5 is multiplied by one, one is obtained.

The reciprocal can also be found for any other integer.

You can also find the reciprocal for any other fraction. To do this, it is enough to turn it over.

Division of a fraction by a number

Let's say we have half a pizza:

Let's divide it equally between two. How many pizzas will each get?

It can be seen that after splitting half of the pizza, two equal pieces were obtained, each of which makes up a pizza. So everyone gets a pizza.

Division of fractions is done using reciprocals. Reciprocals allow you to replace division with multiplication.

To divide a fraction by a number, you need to multiply this fraction by the reciprocal of the divisor.

Using this rule, we will write down the division of our half of the pizza into two parts.

So, you need to divide the fraction by the number 2. Here the dividend is a fraction and the divisor is 2.

To divide a fraction by the number 2, you need to multiply this fraction by the reciprocal of the divisor 2. The reciprocal of the divisor 2 is a fraction. So you need to multiply by

Multiplication and division of fractions.

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

This operation is much nicer than addition-subtraction! Because it's easier. I remind you: to multiply a fraction by a fraction, you need to multiply the numerators (this will be the numerator of the result) and the denominators (this will be the denominator). That is:

For example:

Everything is extremely simple. And please don't look for a common denominator! Don't need it here...

To divide a fraction by a fraction, you need to flip second(this is important!) fraction and multiply them, i.e.:

For example:

If multiplication or division with integers and fractions is caught, it's okay. As with addition, we make a fraction from a whole number with a unit in the denominator - and go! For example:

In high school, you often have to deal with three-story (or even four-story!) fractions. For example:

How to bring this fraction to a decent form? Yes, very easy! Use division through two points:

But don't forget about the division order! Unlike multiplication, this is very important here! Of course, we will not confuse 4:2 or 2:4. But in a three-story fraction it is easy to make a mistake. Please note, for example:

In the first case (expression on the left):

In the second (expression on the right):

Feel the difference? 4 and 1/9!

What is the order of division? Or brackets, or (as here) the length of horizontal dashes. Develop an eye. And if there are no brackets or dashes, like:

then divide-multiply in order, left to right!

And another very simple and important trick. In actions with degrees, it will come in handy for you! Let's divide the unit by any fraction, for example, by 13/15:

The shot has turned over! And it always happens. When dividing 1 by any fraction, the result is the same fraction, only inverted.

That's all the actions with fractions. The thing is quite simple, but gives more than enough errors. Take note of practical advice, and there will be fewer of them (mistakes)!

Practical Tips:

1. The most important thing when working with fractional expressions is accuracy and attentiveness! These are not common words, not good wishes! This is a severe need! Do all the calculations on the exam as a full-fledged task, with concentration and clarity. It is better to write two extra lines in a draft than to mess up when calculating in your head.

2. In examples with different types of fractions - go to ordinary fractions.

3. We reduce all fractions to the stop.

4. We reduce multi-level fractional expressions to ordinary ones using division through two points (we follow the order of division!).

5. We divide the unit into a fraction in our mind, simply by turning the fraction over.

Here are the tasks you need to complete. Answers are given after all tasks. Use the materials of this topic and practical advice. Estimate how many examples you could solve correctly. The first time! Without a calculator! And draw the right conclusions...

Remember the correct answer obtained from the second (especially the third) time - does not count! Such is the harsh life.

So, solve in exam mode ! This is preparation for the exam, by the way. We solve an example, we check, we solve the following. We decided everything - we checked again from the first to the last. But only Then look at the answers.

Calculate:

Did you decide?

Looking for answers that match yours. I specifically wrote them down in a mess, away from the temptation, so to speak ... Here they are, the answers, written down with a semicolon.

0; 17/22; 3/4; 2/5; 1; 25.

And now we draw conclusions. If everything worked out - happy for you! Elementary calculations with fractions are not your problem! You can do more serious things. If not...

So you have one of two problems. Or both at once.) Lack of knowledge and (or) inattention. But this solvable Problems.

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.

T class type: ONZ (discovery of new knowledge - according to the technology of the activity method of teaching).

Basic goals:

1. Deduce methods of dividing a fraction by a natural number;
2. To form the ability to perform the division of a fraction by a natural number;
3. Repeat and consolidate the division of fractions;
4. Train the ability to reduce fractions, analyze and solve problems.

Equipment demo material:

1. Tasks for updating knowledge:

Compare expressions:

Reference:

2. Trial (individual) task.

1. Perform division:

2. Perform the division without performing the entire chain of calculations: .

References:

• When dividing a fraction by a natural number, you can multiply the denominator by this number, and leave the numerator the same.

• If the numerator is divisible by a natural number, then when dividing a fraction by this number, you can divide the numerator by the number, and leave the denominator the same.

During the classes

I. Motivation (self-determination) for learning activities.

Purpose of the stage:

1. Organize the actualization of the requirements for the student on the part of educational activities (“must”);
2. Organize the activities of students to establish a thematic framework (“I can”);
3. To create conditions for the student to have an internal need for inclusion in educational activities (“I want”).

Organization of the educational process at stage I.

Hello! I'm glad to see you all in math class. I hope it's mutual.

Guys, what new knowledge did you acquire in the last lesson? (Divide fractions).

Right. What helps you divide fractions? (Rule, properties).

Where do we need this knowledge? (In examples, equations, tasks).

Well done! You did well in the last lesson. Would you like to discover new knowledge yourself today? (Yes).

Then - go! And the motto of the lesson is the statement “Mathematics cannot be learned by watching how your neighbor does it!”.

II. Actualization of knowledge and fixation of an individual difficulty in a trial action.

Purpose of the stage:

1. To organize the actualization of the studied methods of action, sufficient to build new knowledge. Fix these methods verbally (in speech) and symbolically (standard) and generalize them;
2. Organize the actualization of mental operations and cognitive processes sufficient to build new knowledge;
3. Motivate for a trial action and its independent implementation and justification;
4. Present an individual task for a trial action and analyze it in order to identify new educational content;
5. Organize the fixation of the educational goal and the topic of the lesson;
6. Organize the implementation of a trial action and fixing the difficulty;
7. Organize an analysis of the responses received and record individual difficulties in performing a trial action or justifying it.

Organization of the educational process at stage II.

Frontally, using tablets (individual boards).

1. Compare expressions:

(These expressions are equal)

What interesting things did you notice? (The numerator and denominator of the dividend, the numerator and denominator of the divisor in each expression increased by the same number of times. Thus, the dividends and divisors in the expressions are represented by fractions that are equal to each other).

Find the meaning of the expression and write it down on the tablet. (2)

How to write this number as a fraction?

How did you perform the division action? (Children pronounce the rule, the teacher hangs letters on the board)

2. Calculate and record only the results:

3. Add up your results and write down your answer. (2)

What is the name of the number obtained in task 3? (Natural)

Do you think you can divide a fraction by a natural number? (Yes, we will try)

Try this.

4. Individual (trial) task.

Do the division: (example a only)

What rule did you use to divide? (According to the rule of dividing a fraction by a fraction)

And now divide the fraction by a natural number in a simpler way, without performing the entire chain of calculations: (example b). I give you 3 seconds for this.

Who failed to complete the task in 3 seconds?

Who made it? (There are no such)

Why? (We don't know the way)

What did you get? (Difficulty)

What do you think we will do in class? (Divide fractions by natural numbers)

That's right, open your notebooks and write down the topic of the lesson "Dividing a fraction by a natural number."

Why does this topic sound new when you already know how to divide fractions? (Need a new way)

Right. Today we will establish a technique that simplifies the division of a fraction by a natural number.

III. Identification of the location and cause of the difficulty.

Purpose of the stage:

1. Organize the restoration of completed operations and fix (verbal and symbolic) place - step, operation, where the difficulty arose;
2. To organize the correlation of students' actions with the method (algorithm) used and the fixation in external speech of the cause of the difficulty - those specific knowledge, skills or abilities that are not enough to solve the initial problem of this type.

Organization of the educational process at stage III.

What task did you have to complete? (Divide a fraction by a natural number without doing the whole chain of calculations)

What caused you difficulty? (Could not solve in a short time in a fast way)

What is the purpose of our lesson? (Find a quick way to divide a fraction by a natural number)

What will help you? (Already known rule for dividing fractions)

IV. Construction of the project of an exit from difficulty.

Purpose of the stage:

1. Clarification of the purpose of the project;
2. Choice of method (clarification);
3. Definition of funds (algorithm);
4. Building a plan to achieve the goal.

Organization of the educational process at stage IV.

Let's go back to the test case. Did you say that you divided by the rule of dividing fractions? (Yes)

To do this, replace a natural number with a fraction? (Yes)

What step(s) do you think you can skip?

(The solution chain is open on the board:

Analyze and draw a conclusion. (Step 1)

If there is no answer, then we summarize through the questions:

Where did the natural divisor go? (to the denominator)

Has the numerator changed? (No)

So what step can be "omitted"? (Step 1)

Action plan:

• Multiply the denominator of a fraction by a natural number.
• The numerator does not change.
• We get a new fraction.

V. Implementation of the constructed project.

Purpose of the stage:

1. Organize communicative interaction in order to implement the constructed project aimed at acquiring the missing knowledge;
2. Organize the fixation of the constructed method of action in speech and signs (with the help of a standard);
3. Organize the solution of the original problem and record the overcoming of the difficulty;
4. Organize a clarification of the general nature of the new knowledge.

Organization of the educational process at stage V.

Now run the test case in the new way quickly.

Are you able to complete the task quickly now? (Yes)

Explain how you did it? (Children speak)

This means that we have received new knowledge: the rule for dividing a fraction by a natural number.

Well done! Say it in pairs.

Then one student speaks to the class. We fix the rule-algorithm verbally and in the form of a standard on the board.

Now enter the letter designations and write down the formula for our rule.

The student writes on the board, pronouncing the rule: when dividing a fraction by a natural number, you can multiply the denominator by this number, and leave the numerator the same.

(Everyone writes the formula in notebooks).

And now once again analyze the chain of solving the trial task, paying special attention to the answer. What did they do? (The numerator of the fraction 15 was divided (reduced) by the number 3)

What is this number? (Natural, divisor)

So how else can you divide a fraction by a natural number? (Check: if the numerator of a fraction is divisible by this natural number, then you can divide the numerator by this number, write the result into the numerator of the new fraction, and leave the denominator the same)

Write this method in the form of a formula. (The student writes down the rule on the board. Everyone writes down the formula in notebooks.)

Let's go back to the first method. Can it be used if a:n? (Yes, this is the general way)

And when is the second method convenient to use? (When the numerator of a fraction is divisible by a natural number without a remainder)

VI. Primary consolidation with pronunciation in external speech.

Purpose of the stage:

1. To organize the assimilation by children of a new method of action when solving typical problems with their pronunciation in external speech (frontally, in pairs or groups).

Organization of the educational process at stage VI.

Calculate in a new way:

• No. 363 (a; d) - perform at the blackboard, pronouncing the rule.
• No. 363 (d; f) - in pairs with a check on the sample.

VII. Independent work with self-test according to the standard.

Purpose of the stage:

1. To organize the students' independent fulfillment of tasks for a new mode of action;
2. Organize self-test based on comparison with the standard;
3. Based on the results of independent work, organize a reflection on the assimilation of a new mode of action.

Organization of the educational process at stage VII.

Calculate in a new way:

• No. 363 (b; c)

Students check the standard, note the correctness of the performance. The causes of errors are analyzed and errors are corrected.

The teacher asks those students who made mistakes, what is the reason?

At this stage, it is important that each student independently check their work.

VIII. Inclusion in the system of knowledge and repetition.

Purpose of the stage:

1. Organize the identification of the boundaries of the application of new knowledge;
2. Organize the repetition of educational content necessary to ensure meaningful continuity.

Organization of the educational process at stage VIII.

Organize the fixation of unresolved difficulties in the lesson as a direction for future learning activities;

Organize discussion and recording of homework.

Organization of the educational process at stage IX.

1. Dialogue:

Guys, what new knowledge did you discover today? (We learned to divide a fraction by a natural number in a simple way)

Formulate a general way. (They say)

In what way, and in what cases can you still use it? (They say)

What is the advantage of the new method?

Have we reached our goal of the lesson? (Yes)

What knowledge did you use to achieve the goal? (They say)

Have you succeeded?

What were the difficulties?

2. Homework: clause 3.2.4.; No. 365 (l, n, o, p); No. 370.

3. Teacher: I am glad that today everyone was active, managed to find a way out of the difficulty. And most importantly, they were not neighbors when a new one was opened and consolidated. Thanks for the lesson kids!

Ordinary fractional numbers first meet schoolchildren in the 5th grade and accompany them throughout their lives, since in everyday life it is often necessary to consider or use some object not entirely, but in separate pieces. The beginning of the study of this topic - share. Shares are equal parts into which an object is divided. After all, it is not always possible to express, for example, the length or price of a product as an integer; one should take into account parts or shares of any measure. Formed from the verb "to crush" - to divide into parts, and having Arabic roots, in the VIII century the word "fraction" itself appeared in Russian.

Fractional expressions have long been considered the most difficult section of mathematics. In the 17th century, when first textbooks in mathematics appeared, they were called "broken numbers", which was very difficult to display in people's understanding.

The modern form of simple fractional residues, parts of which are separated precisely by a horizontal line, was first promoted by Fibonacci - Leonardo of Pisa. His writings are dated 1202. But the purpose of this article is to simply and clearly explain to the reader how the multiplication of mixed fractions with different denominators occurs.

Multiplying fractions with different denominators

Initially, it is necessary to determine varieties of fractions:

• correct;
• wrong;
• mixed.

Next, you need to remember how fractional numbers with the same denominators are multiplied. The very rule of this process is easy to formulate independently: the result of multiplying simple fractions with the same denominators is a fractional expression, the numerator of which is the product of the numerators, and the denominator is the product of the denominators of these fractions. That is, in fact, the new denominator is the square of one of the existing ones initially.

When multiplying simple fractions with different denominators for two or more factors, the rule does not change:

a/b * c/d = a*c / b*d.

The only difference is that the formed number under the fractional bar will be the product of different numbers and, of course, it cannot be called the square of one numerical expression.

It is worth considering the multiplication of fractions with different denominators using examples:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 <> 2*3 / 3*7 = 6/ 21 .

The examples use ways to reduce fractional expressions. You can reduce only the numbers of the numerator with the numbers of the denominator; adjacent factors above or below the fractional bar cannot be reduced.

Along with simple fractional numbers, there is the concept of mixed fractions. A mixed number consists of an integer and a fractional part, that is, it is the sum of these numbers:

1 4/ 11 =1 + 4/ 11.

How does multiplication work?

Several examples are provided for consideration.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

The example uses the multiplication of a number by ordinary fractional part, you can write down the rule for this action by the formula:

a * b/c = a*b /c.

In fact, such a product is the sum of identical fractional remainders, and the number of terms indicates this natural number. Special case:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

There is another option for solving the multiplication of a number by a fractional remainder. Simply divide the denominator by this number:

d* e/f = e/f: d.

It is useful to use this technique when the denominator is divided by a natural number without a remainder or, as they say, completely.

Convert mixed numbers to improper fractions and get the product in the previously described way:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

This example involves a way to represent a mixed fraction as an improper fraction, it can also be represented as a general formula:

a bc = a*b+ c / c, where the denominator of the new fraction is formed by multiplying the integer part with the denominator and adding it to the numerator of the original fractional remainder, and the denominator remains the same.

This process also works in reverse. To select the integer part and the fractional remainder, you need to divide the numerator of an improper fraction by its denominator with a “corner”.

Multiplication of improper fractions produced in the usual way. When the entry goes under a single fractional line, as necessary, you need to reduce the fractions in order to reduce the numbers using this method and it is easier to calculate the result.

There are many assistants on the Internet to solve even complex mathematical problems in various program variations. A sufficient number of such services offer their help in calculating the multiplication of fractions with different numbers in the denominators - the so-called online calculators for calculating fractions. They are able not only to multiply, but also to perform all other simple arithmetic operations with ordinary fractions and mixed numbers. It is not difficult to work with it, the corresponding fields are filled in on the site page, the sign of the mathematical action is selected and “calculate” is pressed. The program counts automatically.

The topic of arithmetic operations with fractional numbers is relevant throughout the education of middle and senior schoolchildren. In high school, they are no longer considering the simplest species, but integer fractional expressions, but the knowledge of the rules for transformation and calculations, obtained earlier, is applied in its original form. Well-learned basic knowledge gives full confidence in the successful solution of the most complex tasks.

In conclusion, it makes sense to cite the words of Leo Tolstoy, who wrote: “Man is a fraction. It is not in the power of man to increase his numerator - his merits, but everyone can decrease his denominator - his opinion of himself, and by this decrease come closer to his perfection.

Last time we learned how to add and subtract fractions (see the lesson "Addition and subtraction of fractions"). The most difficult moment in those actions was bringing fractions to a common denominator.

Now it's time to deal with multiplication and division. The good news is that these operations are even easier than addition and subtraction. To begin with, consider the simplest case, when there are two positive fractions without a distinguished integer part.

To multiply two fractions, you need to multiply their numerators and denominators separately. The first number will be the numerator of the new fraction, and the second will be the denominator.

To divide two fractions, you need to multiply the first fraction by the "inverted" second.

Designation:

From the definition it follows that the division of fractions is reduced to multiplication. To flip a fraction, just swap the numerator and denominator. Therefore, the entire lesson we will consider mainly multiplication.

As a result of multiplication, a reduced fraction can arise (and often does arise) - of course, it must be reduced. If, after all the reductions, the fraction turned out to be incorrect, the whole part should be distinguished in it. But what exactly will not happen with multiplication is reduction to a common denominator: no crosswise methods, maximum factors and least common multiples.

By definition we have:

Multiplication of fractions with an integer part and negative fractions

If there is an integer part in the fractions, they must be converted to improper ones - and only then multiplied according to the schemes outlined above.

If there is a minus in the numerator of a fraction, in the denominator or in front of it, it can be taken out of the limits of multiplication or removed altogether according to the following rules:

1. Plus times minus gives minus;
2. Two negatives make an affirmative.

Until now, these rules have only been encountered when adding and subtracting negative fractions, when it was required to get rid of the whole part. For a product, they can be generalized in order to “burn” several minuses at once:

1. We cross out the minuses in pairs until they completely disappear. In an extreme case, one minus can survive - the one that did not find a match;
2. If there are no minuses left, the operation is completed - you can start multiplying. If the last minus is not crossed out, since it did not find a pair, we take it out of the limits of multiplication. You get a negative fraction.

Task. Find the value of the expression:

We translate all fractions into improper ones, and then we take out the minuses outside the limits of multiplication. What remains is multiplied according to the usual rules. We get:

Let me remind you once again that the minus that comes before a fraction with a highlighted integer part refers specifically to the entire fraction, and not just to its integer part (this applies to the last two examples).

Also pay attention to negative numbers: when multiplied, they are enclosed in brackets. This is done in order to separate the minuses from the multiplication signs and make the whole notation more accurate.

Reducing fractions on the fly

Multiplication is a very laborious operation. The numbers here are quite large, and to simplify the task, you can try to reduce the fraction even more before multiplication. Indeed, in essence, the numerators and denominators of fractions are ordinary factors, and, therefore, they can be reduced using the basic property of a fraction. Take a look at the examples:

Task. Find the value of the expression:

By definition we have:

In all examples, the numbers that have been reduced and what is left of them are marked in red.

Please note: in the first case, the multipliers were reduced completely. Units remained in their place, which, generally speaking, can be omitted. In the second example, it was not possible to achieve a complete reduction, but the total amount of calculations still decreased.

However, in no case do not use this technique when adding and subtracting fractions! Yes, sometimes there are similar numbers that you just want to reduce. Here, look:

You can't do that!

The error occurs due to the fact that when adding a fraction, the sum appears in the numerator of a fraction, and not the product of numbers. Therefore, it is impossible to apply the main property of a fraction, since this property deals specifically with the multiplication of numbers.

There is simply no other reason to reduce fractions, so the correct solution to the previous problem looks like this:

Correct solution:

As you can see, the correct answer turned out to be not so beautiful. In general, be careful.