September 19th, 2009
Tesseract (from other Greek τέσσερες ἀκτῖνες - four rays) - a four-dimensional hypercube - an analogue of a cube in four-dimensional space.
The image is a projection (perspective) of a four-dimensional cube onto a three-dimensional space.
According to the Oxford Dictionary, the word "tesseract" was coined and used in 1888 by Charles Howard Hinton (1853-1907) in his book A New Age of Thought. Later, some people called the same figure "tetracube".
Geometry
An ordinary tesseract in Euclidean four-dimensional space is defined as the convex hull of points (±1, ±1, ±1, ±1). In other words, it can be represented as the following set:
The tesseract is limited by eight hyperplanes, the intersection of which with the tesseract itself defines its three-dimensional faces (which are ordinary cubes). Each pair of non-parallel 3D faces intersect to form 2D faces (squares), and so on. Finally, a tesseract has 8 3D faces, 24 2D, 32 edges and 16 vertices.
Popular Description
Let's try to imagine how the hypercube will look without leaving the three-dimensional space.
In one-dimensional "space" - on a line - we select a segment AB of length L. On a two-dimensional plane at a distance L from AB, we draw a segment DC parallel to it and connect their ends. Get the square ABCD. Repeating this operation with a plane, we get a three-dimensional cube ABCDHEFG. And by shifting the cube in the fourth dimension (perpendicular to the first three) by a distance L, we get the hypercube ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Build_tesseract.PNG
The one-dimensional segment AB serves as a side of the two-dimensional square ABCD, the square is the side of the cube ABCDHEFG, which, in turn, will be the side of the four-dimensional hypercube. A straight line segment has two boundary points, a square has four vertices, and a cube has eight. Thus, in a four-dimensional hypercube, there will be 16 vertices: 8 vertices of the original cube and 8 vertices shifted in the fourth dimension. It has 32 edges - 12 each give the initial and final positions of the original cube, and 8 more edges "draw" eight of its vertices that have moved into the fourth dimension. The same reasoning can be done for the faces of the hypercube. In two-dimensional space, it is one (the square itself), the cube has 6 of them (two faces from the moved square and four more will describe its sides). A four-dimensional hypercube has 24 square faces - 12 squares of the original cube in two positions and 12 squares from twelve of its edges.
In a similar way, we can continue the reasoning for hypercubes of a larger number of dimensions, but it is much more interesting to see how a four-dimensional hypercube will look like for us, inhabitants of three-dimensional space. Let us use for this the already familiar method of analogies.
Tesseract unfolding
Let's take the wire cube ABCDHEFG and look at it with one eye from the side of the face. We will see and can draw two squares on the plane (its near and far faces), connected by four lines - side edges. Similarly, a four-dimensional hypercube in three-dimensional space will look like two cubic "boxes" inserted into each other and connected by eight edges. In this case, the "boxes" themselves - three-dimensional faces - will be projected onto "our" space, and the lines connecting them will stretch in the fourth dimension. You can also try to imagine a cube not in projection, but in a spatial image.
Just as a three-dimensional cube is formed by a square shifted by the length of a face, a cube shifted into the fourth dimension will form a hypercube. It is limited by eight cubes, which in the future will look like some rather complex figure. Its part, which remained in “our” space, is drawn with solid lines, and the part that went into hyperspace is dashed. The four-dimensional hypercube itself consists of an infinite number of cubes, just as a three-dimensional cube can be “cut” into an infinite number of flat squares.
By cutting six faces of a three-dimensional cube, you can decompose it into a flat figure - a net. It will have a square on each side of the original face, plus one more - the face opposite to it. A three-dimensional development of a four-dimensional hypercube will consist of the original cube, six cubes that “grow” from it, plus one more - the final “hyperface”.
The properties of a tesseract are an extension of the properties of geometric figures of a smaller dimension into a four-dimensional space.
projections
to two-dimensional space
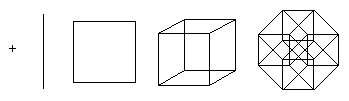
This structure is hard to imagine, but it is possible to project a tesseract into 2D or 3D spaces. In addition, projection onto a plane makes it easy to understand the location of the vertices of the hypercube. In this way, images can be obtained that no longer reflect the spatial relationships within the tesseract, but which illustrate the vertex link structure, as in the following examples:
to three-dimensional space
The projection of the tesseract onto three-dimensional space is two nested three-dimensional cubes, the corresponding vertices of which are connected by segments. The inner and outer cubes have different sizes in 3D space, but they are equal cubes in 4D space. To understand the equality of all cubes of the tesseract, a rotating model of the tesseract was created.
Six truncated pyramids along the edges of the tesseract are images of equal six cubes.
stereo pair
A stereopair of a tesseract is depicted as two projections onto three-dimensional space. This depiction of the tesseract was designed to represent depth as a fourth dimension. The stereo pair is viewed so that each eye sees only one of these images, a stereoscopic picture arises that reproduces the depth of the tesseract.
Tesseract unfolding
The surface of a tesseract can be unfolded into eight cubes (similar to how the surface of a cube can be unfolded into six squares). There are 261 different unfoldings of the tesseract. The unfoldings of a tesseract can be calculated by plotting the connected corners on the graph.
Tesseract in art
In Edwine A. Abbott's New Plain, the hypercube is the narrator.
In one episode of The Adventures of Jimmy Neutron: "Boy Genius", Jimmy invents a four-dimensional hypercube identical to the foldbox from Heinlein's 1963 Glory Road.
Robert E. Heinlein has mentioned hypercubes in at least three science fiction stories. In The House of Four Dimensions (The House That Teel Built) (1940), he described a house built as an unfolding of a tesseract.
In Heinlein's novel Glory Road, hyper-sized dishes are described that were larger on the inside than on the outside.
Henry Kuttner's short story "Mimsy Were the Borogoves" describes an educational toy for children from the distant future, similar in structure to the tesseract.
In the novel by Alex Garland (1999), the term "tesseract" is used for the three-dimensional unfolding of a four-dimensional hypercube, rather than the hypercube itself. This is a metaphor designed to show that the cognizing system should be wider than the cognizable one.
The plot of Cube 2: Hypercube centers on eight strangers trapped in a "hypercube", or network of connected cubes.
The TV series Andromeda uses tesseract generators as a conspiracy device. They are primarily intended to control space and time.
The painting "Crucifixion" (Corpus Hypercubus) by Salvador Dali (1954)
The Nextwave comic book depicts a vehicle that includes 5 tesseract zones.
In the album Voivod Nothingface, one of the songs is called "In my hypercube".
In Anthony Pierce's novel Route Cube, one of IDA's orbital moons is called a tesseract that has been compressed into 3 dimensions.
In the series "School" Black Hole "" in the third season there is an episode "Tesseract". Lucas presses the secret button and the school begins to take shape like a mathematical tesseract.
The term "tesseract" and the term "tesse" derived from it is found in Madeleine L'Engle's story "Wrinkle of Time"
Hypercube and Platonic Solids
Simulate a truncated icosahedron (“soccer ball”) in the “Vector” system
where each pentagon is bounded by hexagons
Truncated icosahedron can be obtained by cutting 12 vertices to form faces in the form of regular pentagons. In this case, the number of vertices of the new polyhedron increases by 5 times (12 × 5 = 60), 20 triangular faces turn into regular hexagons (in total faces becomes 20+12=32), A the number of edges increases to 30+12×5=90.







Steps for constructing a truncated icosahedron in the Vector system
Figures in 4-dimensional space.
 --à
--à

 --à
?
--à
?
For example, given a cube and a hypercube. There are 24 faces in a hypercube. This means that a 4-dimensional octahedron will have 24 vertices. Although no, the hypercube has 8 faces of cubes - in each center is a vertex. This means that a 4-dimensional octahedron will have 8 vertices of that one easier.


4-dimensional octahedron. It consists of eight equilateral and equal tetrahedra,
connected four at each vertex.






Rice. An attempt to simulate
hyperball-hypersphere in the "Vector" system
Front - back faces - balls without distortion. Another six balls - can be specified through ellipsoids or quadratic surfaces (through 4 contour lines as generators) or through faces (first defined through generators).


More tricks to "build" a hypersphere
- the same "soccer ball" in 4-dimensional space
Annex 2
For convex polyhedra, there is a property relating the number of its vertices, edges, and faces, proved in 1752 by Leonhard Euler, and called Euler's theorem.
Before formulating it, consider the polyhedra known to us and fill in the following table, in which B is the number of vertices, P - edges and G - faces of a given polyhedron:
|
The name of the polyhedron |
|||
|
triangular pyramid |
|||
|
quadrangular pyramid |
|||
|
triangular prism |
|||
|
quadrangular prism |
|||
|
n-coal pyramid |
n+1 |
2n |
n+1 |
|
n-carbon prism |
2n |
3n |
n+2 |
|
n-carbon truncated pyramid |
2n |
3n |
n+2 |
It is directly seen from this table that for all the chosen polyhedra the equality B - P + T = 2 holds. It turns out that this equality is true not only for these polyhedra, but also for an arbitrary convex polyhedron.
Euler's theorem. For any convex polyhedron, the equality
V - R + G \u003d 2,
where B is the number of vertices, P is the number of edges, and G is the number of faces of the given polyhedron.
Proof. To prove this equality, imagine the surface of a given polyhedron made of an elastic material. Let's delete (cut out) one of its faces and stretch the remaining surface on a plane. We get a polygon (formed by the edges of the removed face of the polyhedron), divided into smaller polygons (formed by the remaining faces of the polyhedron).
Note that polygons can be deformed, enlarged, reduced, or even bent their sides, as long as the sides do not break. The number of vertices, edges and faces will not change.
Let us prove that the resulting partition of a polygon into smaller polygons satisfies the equality
(*) V - R + G "= 1,
where B is the total number of vertices, P is the total number of edges, and Г "is the number of polygons included in the partition. It is clear that Г" \u003d Г - 1, where Г is the number of faces of this polyhedron.
Let us prove that the equality (*) does not change if we draw a diagonal in some polygon of the given partition (Fig. 5, a). Indeed, after drawing such a diagonal, the new partition will have B vertices, P + 1 edges, and the number of polygons will increase by one. Therefore, we have
V - (R + 1) + (G "+1) \u003d V - R + G" .

Using this property, we draw diagonals dividing the incoming polygons into triangles, and for the resulting partition we show that the equality (*) is satisfied (Fig. 5, b). To do this, we will consistently remove the outer edges, reducing the number of triangles. In this case, two cases are possible:
a) to remove the triangle ABC it is required to remove two ribs, in our case AB And BC;
b) to remove the triangleMKNit is required to remove one edge, in our caseMN.
In both cases, the equality (*) will not change. For example, in the first case, after removing the triangle, the graph will consist of B - 1 vertices, R - 2 edges and G "- 1 polygon:
(B - 1) - (P + 2) + (G "- 1) \u003d B - R + G".
Consider the second case for yourself.
Thus, removing one triangle does not change the equality (*). Continuing this process of removing triangles, we will eventually arrive at a partition consisting of a single triangle. For such a partition, B \u003d 3, P \u003d 3, Г "= 1 and, therefore, B - Р + Г" = 1. Hence, equality (*) also holds for the original partition, from which we finally obtain that for a given polygon partition equality (*) holds true. Thus, for the original convex polyhedron, the equality B - P + G = 2 is true.
An example of a polyhedron for which the Euler relation does not hold is shown in Figure 6. This polyhedron has 16 vertices, 32 edges and 16 faces. Thus, for this polyhedron, the equality B - P + G = 0 is satisfied.
Appendix 3
Movie Cube 2: Hypercube "(eng. Cube 2: Hypercube) - a fantasy film, a continuation of the movie" Cube ".
Eight strangers wake up in cube-shaped rooms. The rooms are inside a four-dimensional hypercube. The rooms are constantly moving by "quantum teleportation", and if you climb into the next room, then it is unlikely to return to the previous one. Parallel worlds intersect in the hypercube, time flows differently in some rooms, and some rooms are death traps.
The plot of the picture largely repeats the story of the first part, which is also reflected in the images of some characters. In the rooms of the hypercube, Nobel laureate Rosenzweig dies, who calculated the exact time of the destruction of the hypercube.
Criticism
If in the first part people imprisoned in a labyrinth tried to help each other, in this film it's every man for himself. There are a lot of extra special effects (they are also traps) that do not logically connect this part of the film with the previous one. That is, it turns out the film Cube 2 is a kind of labyrinth of the future 2020-2030, but not 2000. In the first part, all types of traps can theoretically be created by a person. In the second part, these traps are a program of some kind of computer, the so-called "Virtual Reality".
In geometry hypercube- This n-dimensional analogy of a square ( n= 2) and cube ( n= 3). This is a closed convex figure, consisting of groups of parallel lines located on opposite edges of the figure, and connected to each other at right angles.
This figure is also known as tesseract(tesseract). The tesseract is to the cube as the cube is to the square. More formally, a tesseract can be described as a regular convex four-dimensional polytope (polytope) whose boundary consists of eight cubic cells.
According to the Oxford English Dictionary, the word "tesseract" was coined in 1888 by Charles Howard Hinton and used in his book A New Era of Thought. The word was formed from the Greek "τεσσερες ακτινες" ("four rays"), is in the form of four coordinate axes. In addition, in some sources, the same figure was called tetracube(tetracube).
n-dimensional hypercube is also called n-cube.
A point is a hypercube of dimension 0. If you shift a point by a unit of length, you get a segment of unit length - a hypercube of dimension 1. Further, if you shift a segment by a unit of length in a direction perpendicular to the direction of the segment, you get a cube - a hypercube of dimension 2. Shifting the square by a unit of length in the direction perpendicular to the plane of the square, a cube is obtained - a hypercube of dimension 3. This process can be generalized to any number of dimensions. For example, if you shift a cube by a unit of length in the fourth dimension, you get a tesseract.
The family of hypercubes is one of the few regular polyhedra that can be represented in any dimension.
Hypercube elements
Dimension hypercube n has 2 n"sides" (one-dimensional line has 2 points; two-dimensional square - 4 sides; three-dimensional cube - 6 faces; four-dimensional tesseract - 8 cells). The number of vertices (points) of the hypercube is 2 n(for example, for a cube - 2 3 vertices).
Quantity m-dimensional hypercubes on the boundary n-cube equals
For example, on the border of a hypercube there are 8 cubes, 24 squares, 32 edges and 16 vertices.
| n-cube | Name | Vertex (0-face) |
Edge (1-face) |
edge (2-face) |
Cell (3-face) |
(4-face) | (5-face) | (6-face) | (7-face) | (8-face) |
|---|---|---|---|---|---|---|---|---|---|---|
| 0-cube | Dot | 1 | ||||||||
| 1-cube | Line segment | 2 | 1 | |||||||
| 2-cube | Square | 4 | 4 | 1 | ||||||
| 3-cube | Cube | 8 | 12 | 6 | 1 | |||||
| 4-cube | tesseract | 16 | 32 | 24 | 8 | 1 | ||||
| 5-cube | Penteract | 32 | 80 | 80 | 40 | 10 | 1 | |||
| 6-cube | Hexeract | 64 | 192 | 240 | 160 | 60 | 12 | 1 | ||
| 7-cube | Hepteract | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |
| 8-cube | Octeract | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 |
| 9-cube | Eneneract | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 |
Plane projection
The formation of a hypercube can be represented in the following way:
- Two points A and B can be connected to form line segment AB.
- Two parallel segments AB and CD can be connected to form a square ABCD.
- Two parallel squares ABCD and EFGH can be joined to form the cube ABCDEFGH.
- Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to form a hypercube ABCDEFGHIJKLMNOP.
The latter structure is not easy to imagine, but it is possible to depict its projection onto two or three dimensions. Moreover, projections onto a 2D plane can be more useful by rearranging the positions of the projected vertices. In this case, images can be obtained that no longer reflect the spatial relationships of the elements within the tesseract, but illustrate the structure of the vertex connections, as in the examples below.

The first illustration shows how a tesseract is formed in principle by joining two cubes. This scheme is similar to the scheme for creating a cube from two squares. The second diagram shows that all the edges of the tesseract have the same length. This scheme is also forced to look for cubes connected to each other. In the third diagram, the vertices of the tesseract are located in accordance with the distances along the faces relative to the bottom point. This scheme is interesting because it is used as the basic scheme for the network topology of connecting processors in organizing parallel computing: the distance between any two nodes does not exceed 4 edge lengths, and there are many different ways to balance the load.
Hypercube in art
The hypercube has appeared in science fiction since 1940, when Robert Heinlein, in the story "The House That Teal Built" ("And He Built a Crooked House"), described a house built in the shape of a tesseract unfold. In the story, this Further, this house is folded up, turning into a four-dimensional tesseract. After that, the hypercube appears in many books and novels.
Cube 2: Hypercube is about eight people trapped in a network of hypercubes.
The painting Crucifixion (Corpus Hypercubus), 1954 by Salvador Dali depicts Jesus crucified on a tesseract scan. This painting can be seen in the Museum of Art (Metropolitan Museum of Art) in New York.
Conclusion
The hypercube is one of the simplest four-dimensional objects, on the example of which one can see all the complexity and unusualness of the fourth dimension. And what looks impossible in three dimensions is possible in four, for example, impossible figures. So, for example, the bars of an impossible triangle in four dimensions will be connected at right angles. And this figure will look like this from all viewpoints, and will not be distorted, unlike the implementations of the impossible triangle in three-dimensional space (see Fig.
Teachings about multidimensional spaces began to appear in the middle of the 19th century in the works of G. Grassmann, A. Cayley, B. Riemann, W. Clifford, L. Schläfli and other mathematicians. At the beginning of the 20th century, with the advent of A. Einstein's theory of relativity and the ideas of G. Minkowski, physics began to use a four-dimensional space-time coordinate system.
Then science fiction writers borrowed the idea of four-dimensional space from scientists. In their works, they told the world about the amazing wonders of the fourth dimension. The heroes of their works, using the properties of four-dimensional space, could eat the contents of the egg without damaging the shell, drink a drink without opening the cork of the bottle. The kidnappers retrieved the treasure from the safe through the fourth dimension. The links of the chain can be easily disconnected, and the knot on the rope can be untied without touching its ends. Surgeons performed operations on the internal organs without cutting the tissues of the patient's body. The mystics placed the souls of the dead in the fourth dimension. For an ordinary person, the idea of four-dimensional space remained incomprehensible and mysterious, and many generally consider four-dimensional space to be the fruit of the imagination of scientists and science fiction writers, which has nothing to do with reality.
Perception problem
It is traditionally believed that a person cannot perceive and represent four-dimensional figures, since he is a three-dimensional being. The subject perceives three-dimensional figures with the help of the retina, which is two-dimensional. To perceive four-dimensional figures, a three-dimensional retina is needed, but a person does not have such an opportunity.
To get a visual representation of four-dimensional figures, we will use analogies from lower-dimensional spaces for extrapolation to higher-dimensional figures, use the modeling method, apply system analysis methods to search for patterns between elements of four-dimensional figures. The proposed models should adequately describe the properties of four-dimensional figures, do not contradict each other and give a sufficient idea of a four-dimensional figure and, first of all, of its geometric shape. Since there is no systematic and visual description of four-dimensional figures in the literature, but only their names indicating some properties, we propose to start the study of four-dimensional figures with the simplest - a four-dimensional cube, which is called a hypercube.
Hypercube Definition
hypercubea regular polytope is called, the cell of which is a cube.
Polytop is a four-dimensional figure, the boundary of which consists of polyhedra. An analogue of a cell of a polytope is a face of a polyhedron. The hypercube is analogous to a three-dimensional cube.
We will have an idea about the hypercube if we know its properties. The subject perceives some object, representing it in the form of some model. Let's use this method and present the idea of a hypercube in the form of various models.
Analytical Model
We will consider a one-dimensional space (straight line) as an ordered set of pointsM(x), Where xis the coordinate of an arbitrary point on the straight line. Then the unit segment is given by specifying two points:A(0) and B(1).
A plane (two-dimensional space) can be viewed as an ordered set of points M(x; y). The unit square will be completely defined by its four vertices: A(0; 0), B(1; 0), C(1; 1), D(0; 1). The coordinates of the vertices of the square are obtained by adding zero to the coordinates of the segment, and then one.
Three-dimensional space - an ordered set of points M(x; y; z). Eight points are required to define a 3D cube:
A(0; 0; 0), B(1; 0; 0), C(1; 1; 0), D(0; 1; 0),
E(0; 0; 1), F(1; 0; 1), G(1; 1; 1), H(0; 1; 1).
The cube coordinates are obtained from the square coordinates by adding zero and then one.
Four-dimensional space is an ordered set of points M(x; y; z; t). To specify a hypercube, you need to determine the coordinates of its sixteen vertices:
A(0; 0; 0; 0), B(1; 0; 0; 0), C(1; 1; 0; 0), D(0; 1; 0; 0),
E(0; 0; 1; 0), F(1; 0; 1; 0), G(1; 1; 1; 0), H(0; 1; 1; 0),
K(0; 0; 0; 1), L(1; 0; 0; 1), M(1; 1; 0; 1), N(0; 1; 0; 1),
O(0; 0; 1; 1), P(1; 0; 1; 1), R(1; 1; 1; 1), S(0; 1; 1; 1).
The hypercube coordinates are obtained from the coordinates of the 3D cube by adding a fourth coordinate equal to zero and then one.
Using the formulas of analytic geometry for the four-dimensional Euclidean space, one can obtain the properties of a hypercube.
As an example, consider the calculation of the length of the main diagonal of a hypercube. Let it be required to find the distance between points A(0, 0, 0, 0) and R(1, 1, 1, 1). To do this, we use the distance formula in four-dimensional Euclidean space.
In two-dimensional space (on a plane), the distance between points A(x 1 , y 1) and B(x 2 , y 2) is calculated by the formula
This formula follows from the Pythagorean theorem.
The corresponding formula for the distance between points A(x 1 , y 1 , z 1) and B(x 2 , y 2 , z 2) in three-dimensional space has the form
And in one-dimensional space (on a straight line) between points A( x 1) and B( x 2) you can write the corresponding distance formula:
Similarly, the distance between points A(x 1 , y 1 , z 1 , t 1) and B(x 2 , y 2 , z 2 , t 2) in four-dimensional space will be calculated by the formula:
For the proposed example, we find
Thus, the hypercube exists analytically, and its properties can be described no worse than the properties of a three-dimensional cube.
Dynamic Model
The analytical model of a hypercube is very abstract, so let's consider another model - a dynamic one.
A point (a zero-dimensional figure), moving in one direction, generates a segment (a one-dimensional figure). The segment, moving in a direction perpendicular to itself, creates a square (two-dimensional figure). The square, moving in a direction perpendicular to the plane of the square, creates a cube (three-dimensional figure).
The cube, moving perpendicular to the three-dimensional space in which it was originally located, generates a hypercube (four-dimensional figure).
The hypercube boundary is three-dimensional, finite and closed. It consists of a three-dimensional cube in the initial position, a three-dimensional cube in the final position, and six cubes formed by moving the squares of the original cube in the direction of the fourth dimension. The entire boundary of the hypercube consists of 8 three-dimensional cubes (cells).
When moving in the initial position, the cube had 8 vertices and in the final position also 8 vertices. Therefore, the hypercube has a total of 16 vertices.
Four mutually perpendicular edges emanate from each vertex. In total, the hypercube has 32 edges. In the initial position, it had 12 edges, in the final position also 12 edges, and 8 edges formed the tops of the cube when moving in the fourth dimension.
Thus, the border of the hypercube consists of 8 cubes, which consist of 24 squares. Namely, 6 squares in the initial position, 6 in the final position, and 12 squares formed by moving 12 edges in the direction of the fourth dimension.
geometric model
The dynamic model of a hypercube may seem insufficiently clear. Therefore, consider the geometric model of the hypercube. How do we get the geometric model of a 3D cube? We unfold it, and from the unfold we “glue” the cube model. The development of a three-dimensional cube consists of a square, to the sides of which is attached a square plus one more square.  We turn adjacent squares around the sides of the square, and connect the adjacent sides of the squares to each other. And we close the remaining four sides with the last square (Fig. 1).
We turn adjacent squares around the sides of the square, and connect the adjacent sides of the squares to each other. And we close the remaining four sides with the last square (Fig. 1).
Similarly, consider the unfolding of the hypercube. Its development will be a three-dimensional figure, consisting of the original three-dimensional cube, six cubes adjacent to each face of the original cube, and one more cube. There are eight three-dimensional cubes in total (Fig. 2). In order to obtain a four-dimensional cube (hypercube) from this development, each of the adjacent cubes must be rotated by 90 degrees. These adjoining cubes will be located in a different 3D space. Connect adjacent faces (squares) of cubes to each other. Embed the eighth cube with its faces into the remaining unfilled space. We get a four-dimensional figure - a hypercube, the boundary of which consists of eight three-dimensional cubes.
Hypercube image
 It was shown above how to “glue” a hypercube model from a three-dimensional scan. We get images using projection. The central projection of a three-dimensional cube (its image on a plane) looks like this (Fig. 3). Inside the square is another square. The corresponding vertices of the square are connected by segments. Adjacent squares are depicted as trapezoids, although they are squares in 3D space. The inner and outer squares are different sizes, but in real 3D space they are equal squares.
It was shown above how to “glue” a hypercube model from a three-dimensional scan. We get images using projection. The central projection of a three-dimensional cube (its image on a plane) looks like this (Fig. 3). Inside the square is another square. The corresponding vertices of the square are connected by segments. Adjacent squares are depicted as trapezoids, although they are squares in 3D space. The inner and outer squares are different sizes, but in real 3D space they are equal squares.
 Similarly, the central projection of a four-dimensional cube onto three-dimensional space will look like this: inside one cube is another cube. The corresponding vertices of the cubes are connected by segments. The inner and outer cubes have different sizes in 3D space, but they are equal cubes in 4D space (Figure 4).
Similarly, the central projection of a four-dimensional cube onto three-dimensional space will look like this: inside one cube is another cube. The corresponding vertices of the cubes are connected by segments. The inner and outer cubes have different sizes in 3D space, but they are equal cubes in 4D space (Figure 4).
Six truncated pyramids are images of equal six cells (cubes) of a four-dimensional cube.
This three-dimensional projection can be drawn on a plane and you can verify the truth of the properties of the hypercube obtained using the dynamic model.
The hypercube has 16 vertices, 32 edges, 24 faces (squares), 8 cells (cubes). Four mutually perpendicular edges emanate from each vertex. The boundary of the hypercube is a three-dimensional closed convex figure, the volume of which (the side volume of the hypercube) is equal to eight unit three-dimensional cubes. Inside itself, this figure contains a unit hypercube, the hypervolume of which is equal to the hypervolume of the unit hypercube.
Conclusion
In this work, the goal was to give an initial acquaintance with four-dimensional space. This was done on the example of the simplest figure - the hypercube.
The world of four-dimensional space is amazing! In it, along with similar figures in three-dimensional space, there are also figures that have no analogues in three-dimensional space.
Many phenomena of the material world, the macrocosm and the megaworld, despite the grandiose successes in physics, chemistry and astronomy, have remained inexplicable.
There is no single theory that explains all the forces of nature. There is no satisfactory model of the Universe that explains its structure and excludes paradoxes.
By knowing the properties of four-dimensional space and borrowing some ideas from four-dimensional geometry, it will be possible not only to build more rigorous theories and models of the material world, but also to create tools and systems that function according to the laws of the four-dimensional world, then human capabilities will be even more impressive.
Bacalier Maria
The ways of introducing the concept of a four-dimensional cube (tesseract), its structure and some properties are being studied. The question of what three-dimensional objects are obtained when a four-dimensional cube is intersected by hyperplanes parallel to its three-dimensional faces, as well as by hyperplanes perpendicular to its main diagonal. The apparatus of multidimensional analytical geometry used for research is considered.
Download:
Preview:
Introduction……………………………………………………………………….2
Main part………………………………………………………………..4
Conclusions………….. …………………………………………………………..12
References…………………………………………………………..13
Introduction
Four-dimensional space has long attracted the attention of both professional mathematicians and people who are far from practicing this science. Interest in the fourth dimension may be due to the assumption that our three-dimensional world is "immersed" in four-dimensional space, just as a plane is "immersed" in three-dimensional space, a straight line is "immersed" in a plane, and a point is in a straight line. In addition, four-dimensional space plays an important role in the modern theory of relativity (the so-called space-time or Minkowski space), and can also be considered as a special casedimensional Euclidean space (for).
A four-dimensional cube (tesseract) is an object of four-dimensional space that has the maximum possible dimension (just as a regular cube is an object of three-dimensional space). Note that it is also of direct interest, namely, it can appear in optimization problems of linear programming (as an area in which the minimum or maximum of a linear function of four variables is found), and is also used in digital microelectronics (when programming the operation of an electronic clock display). In addition, the very process of studying a four-dimensional cube contributes to the development of spatial thinking and imagination.
Therefore, the study of the structure and specific properties of a four-dimensional cube is quite relevant. It should be noted that in terms of structure, the four-dimensional cube has been studied quite well. Of much greater interest is the nature of its sections by various hyperplanes. Thus, the main purpose of this work is to study the structure of the tesseract, as well as to clarify the question of what three-dimensional objects will be obtained if a four-dimensional cube is cut by hyperplanes parallel to one of its three-dimensional faces, or by hyperplanes perpendicular to its main diagonal. A hyperplane in a four-dimensional space is a three-dimensional subspace. We can say that a straight line on a plane is a one-dimensional hyperplane, a plane in three-dimensional space is a two-dimensional hyperplane.
The goal set determined the objectives of the study:
1) Study the basic facts of multidimensional analytical geometry;
2) To study the features of constructing cubes of dimensions from 0 to 3;
3) Study the structure of a four-dimensional cube;
4) Analytically and geometrically describe a four-dimensional cube;
5) Make models of sweeps and central projections of three-dimensional and four-dimensional cubes.
6) Using the apparatus of multidimensional analytical geometry, describe three-dimensional objects obtained by crossing a four-dimensional cube by hyperplanes parallel to one of its three-dimensional faces, or by hyperplanes perpendicular to its main diagonal.
The information obtained in this way will make it possible to better understand the structure of the tesseract, as well as to reveal a deep analogy in the structure and properties of cubes of various dimensions.
Main part
First, we describe the mathematical apparatus that we will use in the course of this study.
1) Vector coordinates: if, That
2) Equation of a hyperplane with a normal vector looks like here
3) Planes and are parallel if and only if
4) The distance between two points is determined as follows: if, That
5) Condition of orthogonality of vectors:
First of all, let's find out how a four-dimensional cube can be described. This can be done in two ways - geometric and analytical.
If we talk about the geometric method of setting, then it is advisable to follow the process of constructing cubes, starting from zero dimension. A zero-dimensional cube is a point (note, by the way, that a point can also play the role of a zero-dimensional ball). Next, we introduce the first dimension (abscissa axis) and on the corresponding axis we mark two points (two zero-dimensional cubes) located at a distance of 1 from each other. The result is a segment - a one-dimensional cube. Immediately, we note a characteristic feature: The boundary (ends) of a one-dimensional cube (segment) are two zero-dimensional cubes (two points). Next, we introduce the second dimension (y-axis) and on the planeLet's construct two one-dimensional cubes (two segments), the ends of which are at a distance of 1 from each other (in fact, one of the segments is an orthogonal projection of the other). Connecting the corresponding ends of the segments, we get a square - a two-dimensional cube. Again, we note that the boundary of a two-dimensional cube (square) is four one-dimensional cubes (four segments). Finally, we introduce the third dimension (the applicate axis) and construct in spacetwo squares in such a way that one of them is an orthogonal projection of the other (in this case, the corresponding vertices of the squares are at a distance of 1 from each other). Connect the corresponding vertices with segments - we get a three-dimensional cube. We see that the boundary of the three-dimensional cube is six two-dimensional cubes (six squares). The described constructions make it possible to reveal the following regularity: at each stepthe dimensional cube "moves, leaving a trail" inThis is a measurement at a distance of 1, while the direction of movement is perpendicular to the cube. It is the formal continuation of this process that allows us to come to the concept of a four-dimensional cube. Namely, let's force the three-dimensional cube to move in the direction of the fourth dimension (perpendicular to the cube) at a distance of 1. Acting similarly to the previous one, that is, connecting the corresponding vertices of the cubes, we will get a four-dimensional cube. It should be noted that such a construction is geometrically impossible in our space (because it is three-dimensional), but here we do not encounter any contradictions from a logical point of view. Now let's move on to the analytical description of the four-dimensional cube. It is also obtained formally, with the help of analogy. So, the analytical task of a zero-dimensional unit cube has the form:
The analytical task of a one-dimensional unit cube has the form:
The analytical task of a two-dimensional unit cube has the form:
The analytical task of a three-dimensional unit cube has the form:
Now it is very easy to give an analytical representation of a four-dimensional cube, namely:
As you can see, the method of analogies was used for both geometric and analytical methods of specifying a four-dimensional cube.
Now, using the apparatus of analytical geometry, we will find out what structure a four-dimensional cube has. First, let's find out what elements it includes. Here again, you can use the analogy (to put forward a hypothesis). The boundaries of a one-dimensional cube are points (zero-cubes), of a two-dimensional cube - segments (one-dimensional cubes), of a three-dimensional cube - squares (two-dimensional faces). It can be assumed that the boundaries of the tesseract are three-dimensional cubes. In order to prove this, let us clarify what is meant by vertices, edges and faces. The vertices of a cube are its corner points. That is, the coordinates of the vertices can be zeros or ones. Thus, a relationship is found between the dimension of a cube and the number of its vertices. We apply the combinatorial product rule - since the vertexcube has exactlycoordinates, each of which is equal to zero or one (regardless of all the others), then there arepeaks. Thus, at any vertex, all coordinates are fixed and can be equal to or . If we fix all the coordinates (setting each of them equal to or , independently of the others), except for one, then we get straight lines containing the edges of the cube. Similarly to the previous one, we can count that there are exactlythings. And if we now fix all the coordinates (setting each of them equal to or , independently of the others), except for some two, we obtain planes containing two-dimensional faces of the cube. Using the rule of combinatorics, we find that there are exactlythings. Further, similarly - fixing all the coordinates (setting each of them equal to or , regardless of the others), except for some three, we get hyperplanes containing three-dimensional faces of the cube. Using the same rule, we calculate their number - exactlyetc. This will suffice for our study. Let us apply the obtained results to the structure of a four-dimensional cube, namely, in all the derived formulas we set. Therefore, a four-dimensional cube has: 16 vertices, 32 edges, 24 two-dimensional faces, and 8 three-dimensional faces. For clarity, we define analytically all its elements.
Vertices of a four-dimensional cube:
Edges of a four-dimensional cube ():
Two-dimensional faces of a four-dimensional cube (similar restrictions):
Three-dimensional faces of a four-dimensional cube (similar restrictions):
Now that the structure of the four-dimensional cube and the methods of its definition have been described with sufficient completeness, let's proceed to the realization of the main goal - to clarify the nature of the various sections of the cube. Let's start with the elementary case when the sections of a cube are parallel to one of its three-dimensional faces. For example, consider its sections by hyperplanes parallel to the faceIt is known from analytical geometry that any such section will be given by the equationLet us set the corresponding sections analytically:
As you can see, we have obtained an analytical task for a three-dimensional unit cube lying in a hyperplane
To establish an analogy, we write a section of a three-dimensional cube by a plane We get:
This is a square lying in a plane. The analogy is obvious.
Sections of a four-dimensional cube by hyperplanesgive exactly the same results. These will also be single three-dimensional cubes lying in hyperplanes respectively.
Now consider sections of a four-dimensional cube by hyperplanes perpendicular to its main diagonal. Let's solve this problem for a three-dimensional cube first. Using the above-described method of specifying a unit three-dimensional cube, he concludes that, for example, a segment with ends can be taken as the main diagonal And . This means that the vector of the main diagonal will have coordinates. Therefore, the equation of any plane perpendicular to the main diagonal will be:
Let's define the limits of parameter change. Because , then, adding these inequalities term by term, we get:
Or .
If , then (due to restrictions). Similarly, if, That . So, at and at the cutting plane and the cube have exactly one common point ( And respectively). Now let's notice the following. If(again, due to the limitations of the variables). The corresponding planes intersect three faces at once, because, otherwise, the cutting plane would be parallel to one of them, which is not the case by the condition. If, then the plane intersects all faces of the cube. If, then the plane intersects the faces. Let us present the corresponding calculations.
Let Then the planecrosses the line in a straight line, moreover. Border, moreover. edge plane intersects in a straight line, moreover
Let Then the planecrosses the edge:
edge in a straight line, moreover.
edge in a straight line, moreover.
edge in a straight line, moreover.
edge in a straight line, moreover.
edge in a straight line, moreover.
edge in a straight line, moreover.
This time, six segments are obtained, having successively common ends:
Let Then the planecrosses the line in a straight line, moreover. edge plane intersects in a straight line, and . edge plane intersects in a straight line, moreover . That is, three segments are obtained that have pairwise common ends:Thus, for the specified values of the parameterthe plane will intersect the cube in a regular triangle with vertices
So, here is an exhaustive description of the flat figures obtained by crossing the cube with a plane perpendicular to its main diagonal. The main idea was the following. It is necessary to understand which faces the plane intersects, in what sets it intersects them, how these sets are interconnected. For example, if it turned out that the plane intersects exactly three faces along segments that have pairwise common ends, then the section was an equilateral triangle (which is proved by directly counting the lengths of the segments), the vertices of which are these ends of the segments.
Using the same apparatus and the same idea of investigating cross sections, the following facts can be deduced in exactly the same way:
1) The vector of one of the main diagonals of the four-dimensional unit cube has coordinates
2) Any hyperplane perpendicular to the main diagonal of a four-dimensional cube can be written as.
3) In the equation of the secant hyperplane, the parametercan vary from 0 to 4;
4) At and the secant hyperplane and the four-dimensional cube have one common point ( And respectively);
5) When in the section, a regular tetrahedron will be obtained;
6) When in the section, an octahedron will be obtained;
7) When a regular tetrahedron will be obtained in the section.
Accordingly, here the hyperplane intersects the tesseract along the plane, on which, due to the limitations of the variables, a triangular region is allocated (an analogy - the plane intersected the cube along a straight line, on which, due to the limitations of the variables, a segment was allocated). In case 5), the hyperplane intersects exactly four three-dimensional tesseract faces, that is, four triangles are obtained that have pairwise common sides, in other words, forming a tetrahedron (as it can be calculated - correct). In case 6), the hyperplane intersects exactly eight three-dimensional tesseract faces, that is, eight triangles are obtained that have successively common sides, in other words, forming an octahedron. Case 7) is completely similar to case 5).
Let us illustrate what has been said with a concrete example. Namely, we study the section of the four-dimensional cube by the hyperplaneDue to the constraints of the variables, this hyperplane intersects the following 3D faces: edge intersects in a planeDue to the limitations of the variables, we have:Get a triangular area with verticesFurther,we get a triangleAt the intersection of a hyperplane with a facewe get a triangleAt the intersection of a hyperplane with a facewe get a triangleThus, the vertices of the tetrahedron have the following coordinates. As easy to calculate, this tetrahedron is indeed correct.
conclusions
So, in the course of this study, the main facts of multidimensional analytical geometry were studied, the features of constructing cubes of dimensions from 0 to 3 were studied, the structure of a four-dimensional cube was studied, a four-dimensional cube was analytically and geometrically described, models of developments and central projections of three-dimensional and four-dimensional cubes were made, three-dimensional cubes were analytically described objects resulting from the intersection of a four-dimensional cube by hyperplanes parallel to one of its three-dimensional faces, or by hyperplanes perpendicular to its main diagonal.
The study made it possible to reveal a deep analogy in the structure and properties of cubes of various dimensions. The analogy technique used can be applied in the study, for example,dimensional sphere ordimensional simplex. Namely,a dimensional sphere can be defined as a set of pointsdimensional space, equidistant from a given point, which is called the center of the sphere. Further,the dimensional simplex can be defined as the partdimensional space, limited by the minimum numberdimensional hyperplanes. For example, a one-dimensional simplex is a segment (part of one-dimensional space bounded by two points), a two-dimensional simplex is a triangle (part of two-dimensional space bounded by three lines), a three-dimensional simplex is a tetrahedron (part of three-dimensional space bounded by four planes). Finally,the dimensional simplex is defined as the partdimensional space, limitedhyperplane of dimension.
Note that, despite the numerous applications of the tesseract in some areas of science, this study is still largely a mathematical research.
Bibliography
1) Bugrov Ya.S., Nikolsky S.M.Higher mathematics, vol. 1 - M.: Drofa, 2005 - 284 p.
2) Quantum. Four-dimensional cube / Duzhin S., Rubtsov V., No. 6, 1986.
3) Quantum. How to draw dimensional cube / Demidovich N.B., No. 8, 1974.









