Brief theory
Probability theory deals with experiments that can be repeated (at least in theory) an unlimited number of times. Let some experiment be repeated once, and the results of each repetition do not depend on the outcomes of previous repetitions. Such series of repetitions are called independent trials. A special case of such tests are independent Bernoulli trials, which are characterized by two conditions:
1) the result of each test is one of two possible outcomes, called respectively "success" or "failure".
2) the probability of "success" in each subsequent test does not depend on the results of previous tests and remains constant.
Bernoulli's theorem
If a series of independent Bernoulli trials is made, in each of which "success" occurs with probability , then the probability that "success" in the trials occurs exactly once is expressed by the formula:
where is the probability of failure.
- the number of combinations of elements by (see the basic formulas of combinatorics)
This formula is called Bernoulli formula.
The Bernoulli formula allows you to get rid of a large number of calculations - addition and multiplication of probabilities - with a sufficiently large number of tests.
The Bernoulli test scheme is also called the binomial scheme, and the corresponding probabilities are called binomial, which is associated with the use of binomial coefficients.
The distribution according to the Bernoulli scheme allows, in particular, to find the most probable number of occurrence of an event .
If the number of trials n great, then enjoy:
Problem solution example
The task
The germination of seeds of a certain plant is 70%. What is the probability that out of 10 seeds sown: 8, at least 8; at least 8?
The solution of the problem
Let's use the Bernoulli formula:
In our case
Let the event - out of 10 seeds sprout 8:
Let the event - rise at least 8 (that means 8, 9 or 10)
Let the event rise at least 8 (that means 8.9 or 10)
Answer
Medium the cost of solving the control work is 700 - 1200 rubles (but not less than 300 rubles for the entire order). The price is strongly influenced by the urgency of the decision (from days to several hours). The cost of online help in the exam / test - from 1000 rubles. for the ticket solution.
The application can be left directly in the chat, having previously thrown off the condition of the tasks and informing you of the deadlines for solving it. The response time is several minutes.
Bernoulli formula- a formula in probability theory that allows you to find the probability of an event occurring A (\displaystyle A) in independent tests. The Bernoulli formula allows you to get rid of a large number of calculations - addition and multiplication of probabilities - with a sufficiently large number of tests. Named after the outstanding Swiss mathematician Jacob Bernoulli, who derived this formula.
Encyclopedic YouTube
1 / 3
✪ Probability theory. 22. Bernoulli formula. Problem solving
✪ Bernoulli formula
✪ 20 Repeat tests Bernoulli Formula
Subtitles
Wording
Theorem. If the probability p (\displaystyle p) event A (\displaystyle A) is constant in each trial, then the probability P k , n (\displaystyle P_(k,n)) that the event A (\displaystyle A) comes exactly k (\displaystyle k) once a n (\displaystyle n) independent tests is equal to: P k , n = C n k ⋅ p k ⋅ q n − k (\displaystyle P_(k,n)=C_(n)^(k)\cdot p^(k)\cdot q^(n-k)), Where q = 1 − p (\displaystyle q=1-p).
Proof
Let it be held n (\displaystyle n) independent tests, and it is known that as a result of each test, an event A (\displaystyle A) comes with a probability P (A) = p (\displaystyle P\left(A\right)=p) and therefore does not occur with probability P (A ¯) = 1 − p = q (\displaystyle P\left((\bar (A))\right)=1-p=q). Let, also, in the course of probability tests p (\displaystyle p) And q (\displaystyle q) remain unchanged. What is the probability that as a result n (\displaystyle n) independent test, event A (\displaystyle A) comes exactly k (\displaystyle k) once?
It turns out that it is possible to accurately calculate the number of "successful" combinations of test outcomes for which the event A (\displaystyle A) comes k (\displaystyle k) once a n (\displaystyle n) independent trials, is exactly the number combinations of n (\displaystyle n) By k (\displaystyle k) :
C n (k) = n! k! (n − k) ! (\displaystyle C_(n)(k)=(\frac (n{k!\left(n-k\right)!}}} !}.
At the same time, since all trials are independent and their outcomes are incompatible (event A (\displaystyle A) either occurs or not), then the probability of obtaining a "successful" combination is exactly: .
Finally, in order to find the probability that n (\displaystyle n) independent test event A (\displaystyle A) comes exactly k (\displaystyle k) times, you need to add up the probabilities of getting all the "successful" combinations. The probabilities of getting all "successful" combinations are the same and equal p k ⋅ q n − k (\displaystyle p^(k)\cdot q^(n-k)), the number of "successful" combinations is C n (k) (\displaystyle C_(n)(k)), so we finally get:
P k , n = C n k ⋅ p k ⋅ q n − k = C n k ⋅ p k ⋅ (1 − p) n − k (\displaystyle P_(k,n)=C_(n)^(k)\cdot p^( k)\cdot q^(n-k)=C_(n)^(k)\cdot p^(k)\cdot (1-p)^(n-k)).
The last expression is nothing but the Bernoulli formula. It is also useful to note that, due to the completeness of the group of events, it will be true:
∑ k = 0 n (P k , n) = 1 (\displaystyle \sum _(k=0)^(n)(P_(k,n))=1).
Let independent trials be carried out, in each of which the probability of occurrence of an event A is equal to R . In other words, let the Bernoulli scheme take place. Is it possible to predict what will be the approximate relative frequency of occurrence of an event? A positive answer to this question is given by the theorem proved by J. Bernoulli 1 , which was called the "law of large numbers" and laid the foundation for the theory of probability as a science 2 .
Bernoulli's Theorem: If in each of 
independent tests carried out under the same conditions, the probability R
occurrence of an event A
is constant, then the relative frequency of occurrence of the event A
converges in probability to probability R
- the occurrence of a given event in a separate experience, that is,
.
Proof
. So, the Bernoulli scheme takes place, 
. Denote by 
discrete random variable - the number of occurrences of the event A
V 
th test. It is clear that each of the random variables can take only two values: 1
(event A
happened) with a probability R
And 0
(event A
did not occur) with a probability 
, that is
|
|
|
|
|
R |
R |
|
(
)
It's not hard to find
Is it possible to apply Chebyshev's theorem to the quantities under consideration? It is possible if the random variables are pairwise independent and their variances are uniformly limited. Both conditions are met. Indeed, the pairwise independence of quantities 
follows from the fact that the tests are independent. Next 3 
at 
and, consequently, the variances of all quantities are limited, for example, by the number 
. In addition, note that each of the random variables 
when an event occurs A
in the corresponding test takes on a value equal to one. Therefore, the sum 
is equal to the number 
- event occurrences A
V 
trials, which means
,
that is a fraction 
equal to the relative frequency 
event occurrences A
V 
tests.
Then, applying the Chebyshev theorem to the quantities under consideration, we obtain:
Q.E.D.
Comment 1 : Bernoulli's theorem is the simplest special case of Chebyshev's theorem.
Comment 2 : In practice, often unknown probabilities have to be approximately determined from experience, then a large number of experiments were carried out to verify the agreement of Bernoulli's theorem with experience. For example, the 18th century French naturalist Buffon tossed a coin 4040 times. The coat of arms fell out at the same time 2048 times. The frequency of the appearance of the coat of arms in the Buffon experiment is approximately equal to 0.507. The English statistician K. Pearson threw a coin 12,000 times and at the same time observed 6019 coats of arms. The frequency of the coat of arms in this experiment of Pearson is 0.5016. On another occasion he tossed a coin 24,000 times, and the coat of arms fell 12,012 times; the frequency of the loss of the coat of arms in this case turned out to be equal to 0.5005. As you can see, in all the above experiments, the frequency only slightly deviated from the probability of 0.5 - the appearance of a coat of arms as a result of a single toss of a coin.
Comment
3
: It would be wrong, on the basis of Bernoulli's theorem, to conclude that with an increase in the number of trials, the relative frequency steadily tends to the probability R
; in other words, the Bernoulli theorem does not imply the equality
. In the theorem it's just a matter of probability that for a sufficiently large number of trials, the relative frequency will differ arbitrarily little from the constant probability of the occurrence of an event in each trial. Thus, the convergence of the relative frequency 
to probability R
differs from convergence in the sense of conventional analysis. In order to highlight this difference, introduce the concept of "convergence in probability". More precisely, the difference between these types of convergence is as follows: if 
seeks at 
To R
as the limit in the sense of ordinary analysis, then, starting from some 
and for all subsequent values 
, the inequality 
;if 
tends in probability To R
at 
, then for individual values 
inequality may or may not hold.
Poisson and Markov theorems
Noticed if experience conditions change, then the stability property of the relative frequency of occurrence of the event A is saved. This circumstance was proved by Poisson.
Poisson's theorem: With an unlimited increase in the number of independent tests conducted under variable conditions, the relative frequency of occurrence of an event A converges in probability to the arithmetic mean of the probabilities of the occurrence of a given event in each of the experiments, that is
.
Comment 4 : It is easy to see that Poisson's theorem is a special case of Chebyshev's theorem.
THEOREM MARKOV: If the sequence of random variables 
(arbitrarily dependent) is such that when 
,
That, 
condition is met: 
.
Comment
5
: Obviously, if the random variables 
are pairwise independent, then the Markov condition takes the form: for 
.
This shows that Chebyshev's theorem is a special case of Markov's theorem.
Central limit theorem (Lyapunov's theorem)
The considered theorems of the law of large numbers concern the approximation of certain random variables to certain limiting values, regardless of their distribution law. In probability theory, as already noted, there is another group of theorems concerning the limit distribution laws for the sum of random variables. The general name for this group of theorems is central limiting tower. Its various forms differ in the conditions imposed on the sum of the components of random variables. For the first time, one of the forms of the central limit theorem was proved by the outstanding Russian mathematician A.M. Lyapunov in 1900 using the method of characteristic functions specially developed by him.
THEOREM OF LYAPUNOV: The law of distribution of the sum of independent random variables 
approaches the normal distribution law with an unlimited increase 
(that is, when 
) if the following conditions are met:
,
It should be noted that the central limit theorem is valid not only for continuous, but also for discrete random variables. The practical significance of Lyapunov's theorem is enormous. Experience shows that the law of distribution of the sum of independent random variables comparable in their dispersion approaches the normal one fairly quickly. Already with the number of terms of the order of ten, the distribution law of the sum can be replaced by a normal one (in particular, an example of such a sum can be the arithmetic mean of the observed values of random variables, that is 
).
Laplace's theorem is a special case of the central limit theorem. As you remember, it considers the case when the random variables 
are discrete, equally distributed, and take only two possible values: 0 and 1.
Further, the probability that 
included in the interval 
can be calculated using the formula
.
Using the Laplace function, the last formula can be written in a form convenient for calculations:
Where 
.
EXAMPLE. Let some physical quantity be measured. Any measurement gives only an approximate value of the measured quantity, since the measurement result is influenced by many independent random factors (temperature, instrument fluctuations, humidity, etc.). Each of these factors generates a negligible "partial error". However, since the number of these factors is very large, their combined action generates an already noticeable "total error".
Considering the total error as the sum of a very large number of mutually independent partial errors, we can conclude that the total error has a distribution close to normal. Experience confirms the validity of this conclusion.
2 The proof proposed by J. Bernoulli was difficult; a simpler proof was given by P. Chebyshev in 1846.
3 It is known that the product of two factors, the sum of which is a constant value, has the greatest value when the factors are equal.
Repeated independent trials are called Bernoulli trials if each trial has only two possible outcomes and the probabilities of outcomes remain the same for all trials.
Usually these two outcomes are called "success" (S) or "failure" (F) and the corresponding probabilities are denoted p And q. It's clear that p 0, q³ 0 and p+q=1.
The elementary event space of each trial consists of two events Y and H.
Space of elementary events n Bernoulli trials Ω contains 2 n elementary events, which are sequences (chains) of n symbols Y and H. Each elementary event is one of the possible outcomes of the sequence n Bernoulli trials. Since the tests are independent, then, according to the multiplication theorem, the probabilities are multiplied, that is, the probability of any particular sequence is the product obtained by replacing the symbols U and H by p And q respectively, that is, for example: R( )=(U U N U N... N U )= p p q p q ... q q p .
Note that the outcome of the Bernoulli test is often denoted by 1 and 0, and then the elementary event in the sequence n Bernoulli tests - there is a chain consisting of zeros and ones. For example: =(1, 0, 0, ... , 1, 1, 0).
Bernoulli trials are the most important scheme considered in probability theory. This scheme is named after the Swiss mathematician J. Bernoulli (1654-1705), who studied this model in depth in his works.
The main problem that will be of interest to us here is: what is the probability of the event that in n Bernoulli trials happened m success?
If these conditions are met, the probability that, during independent tests, an event 
will be observed exactly m
times (no matter in which experiments), is determined by Bernoulli formula:
(21.1)
Where 
- probability of occurrence 
in every test, and 
is the probability that in a given experience an event 
Did not happen.
If we consider P n (m) as a function m, then it defines a probability distribution, which is called binomial. Let's explore this relationship P n (m) from m, 0£ m£ n.
Events B m ( m
= 0, 1, ..., n) consisting of a different number of occurrences of the event A V n tests, are incompatible and form a complete group. Hence, 
.
Consider the ratio:
=
=
=
.
Hence it follows that P n (m+1)>P n (m), If (n- m)p> (m+1)q, i.e. function P n (m) increases if m< np- q. Likewise, P n (m+1)< P n (m), If (n- m)p< (m+1)q, i.e. P n (m) decreases if m> np- q.
Thus there is a number m 0 , at which P n (m) reaches its highest value. Let's find m 0 .
According to the meaning of the number m 0 we have P n (m 0)³ P n (m 0 -1) and P n (m 0) ³ P n (m 0 +1), hence
,
(21.2)
.
(21.3)
Solving inequalities (21.2) and (21.3) with respect to m 0 , we get:
p/ m 0 ³ q/(n- m 0 +1) Þ m 0 £ np+ p,
q/(n- m 0 ) ³ p/(m 0 +1) Þ m 0 ³ np- q.
So the desired number m 0 satisfies the inequalities
np- q£ m 0 £ np+p. (21.4)
Because p+q=1, then the length of the interval defined by inequality (21.4) is equal to one and there is at least one integer m 0 satisfying the inequalities (21.4):
1) if np - q is an integer, then there are two values m 0 , namely: m 0 = np - q And m 0 = np - q + 1 = np + p;
2) if np - q- fractional, then there is one number m 0 , namely the only integer between the fractional numbers obtained from inequality (21.4);
3) if np is an integer, then there is one number m 0 , namely m 0 = np.
Number m 0 is called the most probable or most probable value (number) of the occurrence of the event A in a series of n independent tests.
In this lesson, we will find the probability of an event occurring in independent trials when the trials are repeated. . Trials are called independent if the probability of one or another outcome of each trial does not depend on what outcomes other trials had. . Independent tests can be carried out both under the same conditions and under different conditions. In the first case, the probability of an event occurring in all trials is the same; in the second case, it varies from trial to trial.
Examples of Independent Retests :
- one of the device nodes or two or three nodes will fail, and the failure of each node does not depend on the other node, and the probability of failure of one node is constant in all tests;
- a part produced under certain constant technological conditions, or three, four, five parts, will turn out to be non-standard, and one part may turn out to be non-standard regardless of any other part, and the probability that the part will turn out to be non-standard is constant in all tests;
- out of several shots on the target, one, three or four shots hit the target regardless of the outcome of other shots and the probability of hitting the target is constant in all trials;
- when the coin is inserted, the machine will operate correctly one, two, or another number of times, regardless of what other coin insertions have had, and the probability that the machine will operate correctly is constant in all trials.
These events can be described by one scheme. Each event occurs in each trial with the same probability, which does not change if the results of previous trials become known. Such tests are called independent, and the scheme is called Bernoulli scheme . It is assumed that such tests can be repeated as many times as desired.
If the probability p event A is constant in each trial, then the probability that in n independent test event A will come m times, located on Bernoulli formula :
(Where q= 1 – p- the probability that the event will not occur)
Let's set the task - to find the probability that an event of this type in n independent trials will come m once.
Bernoulli formula: examples of problem solving
Example 1 Find the probability that among five randomly selected parts two are standard, if the probability that each part is standard is 0.9.
Solution. Event Probability A, consisting in the fact that a part taken at random is standard, is p=0.9 , and the probability that it is non-standard is q=1–p=0.1 . The event indicated in the condition of the problem (we denote it by IN) occurs if, for example, the first two parts are standard, and the next three are non-standard. But the event IN also occurs if the first and third parts are standard and the rest are non-standard, or if the second and fifth parts are standard and the rest are non-standard. There are other possibilities for the event to occur. IN. Any of them is characterized by the fact that out of five parts taken, two, occupying any places out of five, will turn out to be standard. Therefore, the total number of different possibilities for the occurrence of an event IN is equal to the number of possibilities for placing two standard parts in five places, i.e. is equal to the number of combinations of five elements by two, and .
The probability of each possibility, according to the probability multiplication theorem, is equal to the product of five factors, of which two, corresponding to the appearance of standard parts, are equal to 0.9, and the remaining three, corresponding to the appearance of non-standard parts, are equal to 0.1, i.e. this probability is . Since these ten possibilities are incompatible events, by the addition theorem, the probability of an event IN, which we denote
Example 2 The probability that the machine will require the attention of a worker within an hour is 0.6. Assuming that the failures on the machines are independent, find the probability that during an hour the attention of the worker will be required by any one of the four machines serviced by him.
Solution. Using Bernoulli's formula at n=4 , m=1 , p=0.6 and q=1–p=0.4 , we get
Example 3 For the normal operation of the car depot, there must be at least eight cars on the line, and there are ten of them. The probability of non-exit of each car to the line is equal to 0.1. Find the probability of normal operation of the depot in the next day.
Solution. Autobase will work fine (event F) if either or eight will enter the line (the event A), or nine (event IN), or all ten cars event (event C). According to the probability addition theorem,
We find each term according to the Bernoulli formula. Here n=10 , m=8; 10 and p\u003d 1-0.1 \u003d 0.9, since p should mean the probability of a car entering the line; Then q=0.1 . As a result, we get
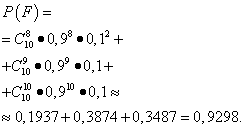
Example 4 Let the probability that a customer needs a size 41 men's shoe be 0.25. Find the probability that out of six buyers at least two need shoes of size 41.
