Šajā nodarbībā mēs apskatīsim vēl divas darbības ar vektoriem: vektoru krustreizinājums un vektoru jauktais produkts (tūlītēja saite tiem, kam tas ir nepieciešams). Tas ir labi, dažreiz gadās, ka pilnīgai laimei, turklāt vektoru punktu reizinājums, vajag arvien vairāk. Tāda ir vektoru atkarība. Var rasties iespaids, ka mēs nonākam analītiskās ģeometrijas džungļos. Tā nav taisnība. Šajā augstākās matemātikas sadaļā parasti ir maz malkas, izņemot, iespējams, pietiekami daudz Pinokio. Patiesībā materiāls ir ļoti izplatīts un vienkāršs – diez vai grūtāks par to pašu skalārais produkts, pat būs mazāk tipisku uzdevumu. Galvenais analītiskajā ģeometrijā, kā daudzi redzēs vai jau ir redzējuši, ir NEMALDĪT APRĒĶINOS. Atkārto kā burvestību, un tu būsi laimīgs =)

Ja vektori kaut kur tālu mirdz kā zibens pie horizonta, tas nav svarīgi, sāciet ar stundu Manekenu vektori atjaunot vai atkārtoti iegūt pamatzināšanas par vektoriem. Gatavāki lasītāji ar informāciju var iepazīties selektīvi, centos apkopot vispilnīgāko piemēru krājumu, kas bieži sastopams praktiskajā darbā

Kas tevi iepriecinās? Kad biju mazs, varēju žonglēt ar divām un pat trīs bumbiņām. Tas izdevās labi. Tagad vispār nav vajadzības žonglēt, jo mēs to apsvērsim tikai telpas vektori, un plakanie vektori ar divām koordinātām tiks izlaisti. Kāpēc? Tā radās šīs darbības – vektoru vektors un jauktais vektoru produkts ir definēts un darbojas trīsdimensiju telpā. Jau vieglāk!

Šajā darbībā tāpat kā skalārajā reizinājumā, divi vektori. Lai tie ir neiznīcīgi burti.

Pati darbība apzīmētsšādā veidā: . Ir arī citi varianti, bet es esmu pieradis vektoru krustenisko reizinājumu apzīmēt šādā veidā, kvadrātiekavās ar krustiņu.

Un uzreiz jautājums: ja iekšā vektoru punktu reizinājums ir iesaistīti divi vektori, un šeit arī tiek reizināti divi vektori kāda ir atšķirība? Skaidra atšķirība, pirmkārt, REZULTĀTĀ:

Vektoru skalārās reizinājuma rezultāts ir SKAITS:

Vektoru krustojuma rezultāts ir VEKTORS: , tas ir, mēs reizinām vektorus un atkal iegūstam vektoru. Slēgts klubs. Patiesībā, līdz ar to arī operācijas nosaukums. Dažādā mācību literatūrā apzīmējumi var arī atšķirties, izmantošu burtu .

Šķērsprodukta definīcija

Vispirms būs definīcija ar bildi, tad komentāri.

Definīcija: krustojums nekolineārs vektori, pieņemts šādā secībā, sauc par VECTOR, garums kas ir skaitliski vienāds ar paralelograma laukumu, kas veidota uz šiem vektoriem; vektors vektoriem ortogonāli, un ir vērsta tā, lai bāzei būtu pareiza orientācija:

Mēs analizējam definīciju pēc kauliem, ir daudz interesantu lietu!

Tātad, mēs varam izcelt šādus būtiskus punktus:

1) Avota vektori pēc definīcijas, kas apzīmēti ar sarkanām bultiņām nav kolineārs. Nedaudz vēlāk būs lietderīgi apsvērt kolineāro vektoru gadījumu.

2) Uzņemtie vektori stingrā kārtībā: – "a" tiek reizināts ar "būt", nevis "būt" uz "a". Vektoru reizināšanas rezultāts ir VECTOR , kas ir apzīmēts ar zilu krāsu. Ja vektorus reizina apgrieztā secībā, tad iegūstam vienāda garuma un virzienā pretēju vektoru (sārtināta krāsa). Tas ir, vienlīdzība .

3) Tagad iepazīsimies ar vektora reizinājuma ģeometrisko nozīmi. Tas ir ļoti svarīgs punkts! Zilā vektora GARUMS (un līdz ar to tumšsarkanā vektora ) ir skaitliski vienāds ar uz vektoriem veidotā paralelograma AREA. Attēlā šis paralelograms ir iekrāsots melnā krāsā.

Piezīme : zīmējums ir shematisks, un, protams, šķērsprodukta nominālais garums nav vienāds ar paralelograma laukumu.

Mēs atceramies vienu no ģeometriskajām formulām: paralelograma laukums ir vienāds ar blakus esošo malu un starp tām esošā leņķa sinusa reizinājumu. Tāpēc, pamatojoties uz iepriekš minēto, ir spēkā formula vektora reizinājuma GARUMA aprēķināšanai:

Es uzsveru, ka formulā mēs runājam par vektora GARU, nevis par pašu vektoru. Kāda ir praktiskā nozīme? Un nozīme ir tāda, ka analītiskās ģeometrijas problēmās paralelograma laukums bieži tiek atrasts, izmantojot vektora reizinājuma jēdzienu:

Mēs iegūstam otro svarīgo formulu. Paralelograma diagonāle (sarkana punktēta līnija) sadala to divos vienādos trīsstūros. Tāpēc trīsstūra laukumu, kas veidots uz vektoriem (sarkans ēnojums), var atrast pēc formulas:

4) Tikpat svarīgs fakts ir tas, ka vektors ir ortogonāls vektoriem, tas ir . Protams, arī pretēji vērstais vektors (sārtināta bultiņa) ir ortogonāls sākotnējiem vektoriem.

5) Vektors ir vērsts tā, lai pamats Tā ir taisnība orientācija. Nodarbībā par pāreja uz jaunu pamatu Es detalizēti runāju par plaknes orientācija, un tagad mēs sapratīsim, kāda ir telpas orientācija. Es paskaidrošu uz jūsu pirkstiem labā roka. Garīgi apvienot rādītājpirksts ar vektoru un Vidējais pirksts ar vektoru. Gredzena pirksts un mazais pirksts nospiediet plaukstā. Rezultātā īkšķis- vektora reizinājums tiks meklēts uz augšu. Šī ir uz labo pusi orientēta bāze (tas ir attēlā). Tagad samainiet vektorus ( rādītājpirksti un vidējie pirksti) vietām, kā rezultātā īkšķis pagriezīsies, un vektorreizinājums jau skatīsies uz leju. Tas ir arī uz labo pusi vērsts pamats. Varbūt jums ir jautājums: kāds pamats ir kreisajai orientācijai? "Piešķirt" tos pašus pirkstus kreisā roka vektori , un iegūstiet kreisās bāzes un kreisās telpas orientāciju (šajā gadījumā īkšķis atradīsies apakšējā vektora virzienā). Tēlaini izsakoties, šīs bāzes “sagriež” jeb orientē telpu dažādos virzienos. Un šo jēdzienu nevajadzētu uzskatīt par kaut ko tālu vai abstraktu - piemēram, visparastākais spogulis maina telpas orientāciju, un, ja jūs “izvelk atstaroto objektu no spoguļa”, tad kopumā tas nebūs iespējams. apvienojiet to ar "oriģinālu". Starp citu, pievelciet trīs pirkstus pie spoguļa un analizējiet atspulgu ;-)

... cik labi, ka jūs tagad zināt par to orientēts pa labi un pa kreisi bāzes, jo dažu pasniedzēju izteikumi par orientācijas maiņu ir šausmīgi =)

Kolineāru vektoru vektorreizinājums

Definīcija ir izstrādāta detalizēti, atliek noskaidrot, kas notiek, ja vektori ir kolineāri. Ja vektori ir kolineāri, tad tos var novietot uz vienas taisnes un arī mūsu paralelograms “salocās” vienā taisnē. Tādu laukums, kā saka matemātiķi, deģenerēts paralelograms ir nulle. Tas pats izriet no formulas - nulles vai 180 grādu sinuss ir vienāds ar nulli, kas nozīmē, ka laukums ir nulle

Tādējādi, ja , tad un . Lūdzu, ņemiet vērā, ka krustreizinājums pats par sevi ir vienāds ar nulles vektoru, taču praksē tas bieži tiek atstāts novārtā un rakstīts, ka arī tas ir vienāds ar nulli.

Īpašs gadījums ir vektora un paša vektora reizinājums:

Izmantojot krustojumu, jūs varat pārbaudīt trīsdimensiju vektoru kolinearitāti, un mēs, cita starpā, arī analizēsim šo problēmu.

Lai atrisinātu praktiskus piemērus, tas var būt nepieciešams trigonometriskā tabula lai no tā atrastu sinusu vērtības.

Nu, iekuram uguni:

1. piemērs

a) Atrodi vektoru vektorreizinājuma garumu, ja

b) Atrodiet uz vektoriem veidota paralelograma laukumu, ja

Lēmums: Nē, tā nav drukas kļūda, es apzināti izveidoju sākotnējos datus nosacījuma vienībās vienādus. Jo risinājumu dizains būs atšķirīgs!

a) Atbilstoši nosacījumam ir jāatrod garums vektors (vektora reizinājums). Saskaņā ar atbilstošo formulu:

Atbilde:

Tā kā tika jautāts par garumu, tad atbildē norādām izmēru - mērvienības.

b) Atbilstoši nosacījumam ir jāatrod kvadrāts uz vektoriem veidots paralelograms . Šī paralelograma laukums ir skaitliski vienāds ar šķērsprodukta garumu:

Atbilde:

Lūdzu, ņemiet vērā, ka atbildē par vektorproduktu vispār nav runas, mums jautāja par to figūras laukums, attiecīgi izmērs ir kvadrāta vienības.

Mēs vienmēr skatāmies, KAS ir jāatrod pēc nosacījuma, un, pamatojoties uz to, mēs formulējam skaidrs atbildi. Var šķist, ka tas ir burtiski, bet skolotāju vidū ir pietiekami daudz literātu, un uzdevums ar labām izredzēm tiks atgriezts pārskatīšanai. Lai gan tas nav īpaši saspringts niķis - ja atbilde ir nepareiza, tad rodas iespaids, ka cilvēks nesaprot vienkāršas lietas un/vai nav sapratis uzdevuma būtību. Šis brīdis vienmēr ir jākontrolē, risinot jebkuru uzdevumu augstākajā matemātikā un arī citos priekšmetos.

Kur pazuda lielais burts "en"? Principā varētu papildus pielipt pie risinājuma, bet, lai saīsinātu ierakstu, es to nedarīju. Es ceru, ka visi to saprot un apzīmē vienu un to pašu.

Populārs risinājuma “dari pats” piemērs:

2. piemērs

Atrodiet uz vektoriem veidota trīsstūra laukumu, ja

Formula trīsstūra laukuma atrašanai caur vektora reizinājumu ir dota definīcijas komentāros. Risinājums un atbilde nodarbības beigās.

Praksē uzdevums patiešām ir ļoti izplatīts, trijstūri parasti var spīdzināt.

Lai atrisinātu citas problēmas, mums ir nepieciešams:

Vektoru krustreizinājuma īpašības

Mēs jau esam apsvēruši dažas vektorprodukta īpašības, tomēr es tās iekļaušu šajā sarakstā.

Patvaļīgiem vektoriem un patvaļīgam skaitlim ir patiesas šādas īpašības:

1) Citos informācijas avotos šis vienums īpašībās parasti nav izdalīts, taču tas ir ļoti svarīgs praktiskā ziņā. Lai tas tā būtu.

2) - īpašums ir apspriests arī iepriekš, dažreiz tas tiek saukts antikommutativitāte. Citiem vārdiem sakot, vektoru secībai ir nozīme.

3) - kombinācija vai asociatīvs vektorproduktu likumi. Konstantes var viegli izņemt no vektora reizinājuma robežām. Tiešām, ko viņi tur dara?

4) - izplatīšana vai izplatīšana vektorproduktu likumi. Arī ar atvēršanu nav problēmu.

Kā demonstrāciju apsveriet īsu piemēru:

3. piemērs

Atrodi, ja

Lēmums: Pēc nosacījuma atkal ir jāatrod vektora reizinājuma garums. Krāsosim savu miniatūru:

(1) Saskaņā ar asociatīvajiem likumiem mēs izņemam konstantes ārpus vektora reizinājuma robežām.

(2) Mēs izņemam konstanti no moduļa, bet modulis “apēd” mīnusa zīmi. Garums nevar būt negatīvs.

(3) Tālāk ir skaidrs.

Atbilde:

Ir pienācis laiks mest malku ugunī:

4. piemērs

Aprēķiniet uz vektoriem veidota trīsstūra laukumu, ja

Lēmums: Atrodiet trīsstūra laukumu, izmantojot formulu . Traucējums ir tāds, ka vektori "ce" un "te" paši ir attēloti kā vektoru summas. Algoritms šeit ir standarta un nedaudz atgādina nodarbības 3. un 4. piemēru. Vektoru punktu reizinājums. Skaidrības labad sadalīsim to trīs posmos:

1) Pirmajā solī mēs izsakām vektora reizinājumu caur vektora reizinājumu, patiesībā, izteikt vektoru vektora izteiksmē. Par garumu vēl ne vārda!

(1) Mēs aizstājam vektoru izteiksmes.

(2) Izmantojot sadalījuma likumus, mēs atveram iekavas saskaņā ar polinomu reizināšanas likumu.

(3) Izmantojot asociatīvos likumus, mēs izņemam visas konstantes ārpus vektora reizinājuma. Ar nelielu pieredzi 2. un 3. darbību var veikt vienlaikus.

(4) Pirmais un pēdējais termins ir vienādi ar nulli (nulles vektors) patīkamās īpašības dēļ. Otrajā termiņā mēs izmantojam vektora reizinājuma antikomutativitātes īpašību:

(5) Mēs piedāvājam līdzīgus terminus.

Rezultātā vektors izrādījās izteikts caur vektoru, kas bija tas, kas bija jāsasniedz:

2) Otrajā solī mēs atrodam vajadzīgā vektora reizinājuma garumu. Šī darbība ir līdzīga 3. piemēram:

3) Atrodiet vajadzīgā trīsstūra laukumu:

Risinājuma 2-3 soļus varētu sakārtot vienā rindā.

Atbilde:

Aplūkotā problēma ir diezgan izplatīta testos, šeit ir piemērs neatkarīgam risinājumam:

5. piemērs

Atrodi, ja

Īss risinājums un atbilde nodarbības beigās. Paskatīsimies, cik uzmanīgs bijāt, pētot iepriekšējos piemērus ;-)

Vektoru krustreizinājums koordinātēs

dots ortonormālā bāzē , tiek izteikts ar formulu:

Formula ir patiešām vienkārša: determinanta augšējā rindā ierakstām koordinātu vektorus, otrajā un trešajā rindā "iepakojam" vektoru koordinātas un ievietojam stingrā kārtībā- vispirms vektora "ve" koordinātas, tad vektora "double-ve" koordinātas. Ja vektori jāreizina citā secībā, tad arī rindas ir jāsamaina:

10. piemērs

Pārbaudiet, vai šādi telpas vektori ir kolineāri:
a)
b)

Lēmums: Testa pamatā ir viens no šīs nodarbības apgalvojumiem: ja vektori ir kolineāri, tad to krustojums ir nulle (nulles vektors): .

a) Atrodiet vektora reizinājumu:

Tātad vektori nav kolineāri.

b) Atrodiet vektora reizinājumu:

Atbilde a) nav kolineārs, b)

Šeit, iespējams, ir visa pamatinformācija par vektoru vektoru reizinājumu.

Šī sadaļa nebūs ļoti liela, jo ir maz problēmu, ja tiek izmantots vektoru jauktais produkts. Patiesībā viss būs atkarīgs no definīcijas, ģeometriskās nozīmes un pāris darba formulām.

Vektoru jauktais reizinājums ir trīs vektoru reizinājums:

Šādi viņi sastājās rindā kā vilciens un gaida, viņi nevar gaidīt, kamēr tiks aprēķināti.

Vispirms atkal definīcija un attēls:

Definīcija: Jaukts produkts ne-kopplanārs vektori, pieņemts šādā secībā, tiek saukts paralēlskaldņa tilpums, veidots uz šiem vektoriem, aprīkots ar "+" zīmi, ja pamats ir pareizs, un "-" zīmi, ja pamats ir pa kreisi.

Taisīsim zīmējumu. Mums neredzamās līnijas ir novilktas ar punktētu līniju:

Iedziļināsimies definīcijā:

2) Uzņemtie vektori noteiktā secībā, tas ir, vektoru permutācija produktā, kā jūs varētu nojaust, nepaliek bez sekām.

3) Pirms komentēt ģeometrisko nozīmi, es atzīmēšu acīmredzamo faktu: vektoru jauktais reizinājums ir SKAITS: . Mācību literatūrā dizains var nedaudz atšķirties, es mēdzu apzīmēt jauktu produktu caur un aprēķinu rezultātu ar burtu "pe".

A-prioritāte jauktais produkts ir paralēlskaldņa tilpums, veidots uz vektoriem (attēls zīmēts ar sarkaniem vektoriem un melnām līnijām). Tas ir, skaitlis ir vienāds ar dotā paralēlskaldņa tilpumu.

Piezīme : Zīmējums ir shematisks.

4) Neraizīsimies atkal ar pamata un telpas orientācijas jēdzienu. Pēdējās daļas nozīme ir tāda, ka skaļumam var pievienot mīnusa zīmi. Vienkārši izsakoties, jauktais produkts var būt negatīvs: .

Formula uz vektoriem veidota paralēlskaldņa tilpuma aprēķināšanai izriet tieši no definīcijas.

7.1. Šķērsprodukta definīcija

Trīs nekopplanāri vektori a , b un c , ņemti norādītajā secībā, veido taisnu trīskāršu, ja no trešā vektora c beigām īsākais pagrieziens no pirmā vektora a uz otro vektoru b ir pretēji pulksteņrādītāja virzienam, un kreiso, ja pulksteņrādītāja virzienā (sk. 16. att.).

Vektora a un vektora b vektorreizinājumu sauc par vektoru c, kas:

1. Perpendikulāri vektoriem a un b, t.i., c ^ a un c ^ b;

2. Tā garums ir skaitliski vienāds ar paralelograma laukumu, kas veidots uz vektoriem a unb kā uz sāniem (skat. 17. att.), t.i.

3. Vektori a , b un c veido taisnu trīskāršu.

Vektora reizinājumu apzīmē ar x b vai [a,b]. No vektora reizinājuma definīcijas tieši izriet šādas attiecības starp ortām, j un k(skat. 18. att.):

i x j \u003d k, j x k \u003d i, k x i \u003d j.
Pierādīsim, piemēram, to i xj \u003d k.

1) k ^ i , k ^ j;

2) |k |=1, bet | i x j| = |i | |J| sin(90°)=1;

3) vektori i , j un k veido labo trīskāršu (skat. 16. att.).

7.2. Krusta produkta īpašības

1. Pārkārtojot faktorus, vektora reizinājums maina zīmi, t.i. un xb \u003d (b xa) (sk. 19. att.).

Vektori a xb un b xa ir kolineāri, tiem ir vienādi moduļi (paralelograma laukums paliek nemainīgs), bet ir vērsti pretēji (pretējas orientācijas trīskārši a, b, a xb un a, b, b x a). Tas ir axb = -(bxa).

2. Vektora reizinājumam ir kombinācijas īpašība attiecībā pret skalāro koeficientu, t.i., l (a xb) \u003d (l a) x b \u003d a x (l b).

Lai l >0. Vektors l (a xb) ir perpendikulārs vektoriem a un b. Vektors ( l a)x b ir arī perpendikulāra vektoriem a un b(vektori a, l bet guļ vienā plaknē). Tātad vektori l(a xb) un ( l a)x b kolineārs. Ir skaidrs, ka viņu virzieni sakrīt. Viņiem ir vienāds garums:

Tāpēc l(a xb)= l a xb. Tas ir pierādīts līdzīgi l<0.

3. Divi nulles vektori a un b ir kolineāri tad un tikai tad, ja to vektora reizinājums ir vienāds ar nulles vektoru, t.i., un ||b<=>un xb \u003d 0.

Jo īpaši i *i =j *j =k *k =0 .

4. Vektora reizinājumam ir sadalījuma īpašība:

(a+b) xs = a xs + b xs .

Pieņem bez pierādījumiem.

7.3. Krusta produkta izteiksme koordinātu izteiksmē

Mēs izmantosim vektoru krustojumu tabulu i , j un k :

ja īsākā ceļa virziens no pirmā vektora uz otro sakrīt ar bultiņas virzienu, tad reizinājums ir vienāds ar trešo vektoru, ja nesakrīt, trešo vektoru ņem ar mīnusa zīmi.

Divi vektori a =a x i +a y j+az k un b=bx i+autors j+bz k. Atradīsim šo vektoru vektorreizinājumu, reizinot tos kā polinomus (atbilstoši vektora reizinājuma īpašībām):

Iegūto formulu var uzrakstīt vēl īsāk:

jo vienādības (7.1) labā puse atbilst trešās kārtas determinanta izvērsumam pirmās rindas elementu izteiksmē Vienādību (7.2) ir viegli atcerēties.

7.4. Daži šķērsprodukta pielietojumi

Vektoru kolinearitātes noteikšana

Paralelograma un trijstūra laukuma atrašana

Saskaņā ar vektoru krustreizinājuma definīciju a un b |a xb | =| a | * |b |sin g , t.i., S par = |a x b |. Un tāpēc D S \u003d 1/2 | a x b |.

Spēka momenta noteikšana par punktu

Pieliek spēku punktā A F = ABļaujiet tai iet O- kāds punkts telpā (skat. 20. att.).

No fizikas ir zināms, ka griezes moments F attiecībā pret punktu O sauc par vektoru M , kas iet caur punktu O un:

1) perpendikulāri plaknei, kas iet caur punktiem O, A, B;

2) skaitliski vienāds ar spēka un pleca reizinājumu

3) veido taisno trīskāršu ar vektoriem OA un A B .

Tāpēc M \u003d OA x F.

Lineārā griešanās ātruma atrašana

Ātrums v punkts M cietam ķermenim, kas rotē ar leņķisko ātrumu w ap fiksētu asi, nosaka ar Eilera formulu v \u003d w x r, kur r \u003d OM, kur O ir kāds fiksēts ass punkts (sk. 21. att.).

Pirms dot vektora reizinājuma jēdzienu, pievērsīsimies jautājumam par vektoru sakārtotā trīskārša a → , b → , c → orientāciju trīsdimensiju telpā.

Sākumā noliksim malā vektorus a → , b → , c → no viena punkta. Trīskārša a → , b → , c → orientācija ir pa labi vai pa kreisi, atkarībā no vektora c → virziena. No virziena, kurā tiek veikts īsākais pagrieziens no vektora a → uz b → no vektora c → gala, tiks noteikta trīskārša a → , b → , c → forma.

Ja īsākā rotācija ir pretēji pulksteņrādītāja virzienam, tad vektoru trīskāršu a → , b → , c → sauc taisnība ja pulksteņrādītāja virzienā - pa kreisi.

Pēc tam ņemam divus nekolineārus vektorus a → un b → . Pēc tam atliksim vektorus A B → = a → un A C → = b → no punkta A. Konstruēsim vektoru A D → = c → , kas vienlaikus ir perpendikulārs gan A B →, gan A C → . Tādējādi, konstruējot vektoru A D → = c →, mēs varam darīt divas lietas, dodot tam vai nu vienu virzienu, vai pretējo (skat. attēlu).

Sakārtotais vektoru trio a → , b → , c → var būt, kā noskaidrojām, pa labi vai pa kreisi atkarībā no vektora virziena.

No iepriekš minētā mēs varam ieviest vektora reizinājuma definīciju. Šī definīcija ir dota diviem vektoriem, kas definēti trīsdimensiju telpas taisnstūrveida koordinātu sistēmā.

1. definīcija

Divu vektoru a → un b → vektorreizinājums mēs sauksim šādu vektoru, kas dots trīsdimensiju telpas taisnstūra koordinātu sistēmā, lai:

• ja vektori a → un b → ir kolineāri, tā būs nulle;
• tas būs perpendikulārs gan vektoram a →​​, gan vektoram b → t.i. ∠ a → c → = ∠ b → c → = π 2 ;
• tā garumu nosaka pēc formulas: c → = a → b → sin ∠ a → , b → ;
• vektoru tripletam a → , b → , c → ir tāda pati orientācija kā dotajai koordinātu sistēmai.

Vektoru a → un b → krustreizinājumam ir šāds apzīmējums: a → × b → .

Šķērsot produktu koordinātas

Tā kā jebkuram vektoram ir noteiktas koordinātes koordinātu sistēmā, ir iespējams ieviest otru vektora reizinājuma definīciju, kas ļaus atrast tā koordinātas no dotajām vektoru koordinātām.

2. definīcija

Trīsdimensiju telpas taisnstūra koordinātu sistēmā divu vektoru a → = (a x ; a y ; a z) un b → = (b x ; b y ; b z) vektoru reizinājums saucam vektoru c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , kur i → , j → , k → ir koordinātu vektori.

Vektora reizinājumu var attēlot kā trešās kārtas kvadrātmatricas determinantu, kur pirmajā rindā ir orta vektori i → , j → , k → , otrajā rindā ir vektora a → koordinātas, bet trešajā. ir vektora b → koordinātes dotajā taisnstūra koordinātu sistēmā, šis matricas determinants izskatās šādi: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Paplašinot šo determinantu pār pirmās rindas elementiem, iegūstam vienādību: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a k → b = = × b y a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Krusta produkta īpašības

Ir zināms, ka vektora reizinājums koordinātēs tiek attēlots kā matricas c → = a → × b → = i → j → k → a x a y a z b x b y b z determinants, tad uz bāzes matricas determinantu īpašības sekojošais vektora produkta īpašības:

1. antikommutativitāte a → × b → = - b → × a → ;
2. sadalījums a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → vai a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. asociativitāte λ a → × b → = λ a → × b → vai a → × (λ b →) = λ a → × b → , kur λ ir patvaļīgs reāls skaitlis.

Šīm īpašībām nav sarežģītu pierādījumu.

Piemēram, mēs varam pierādīt vektora reizinājuma antikommutativitātes īpašību.

Antikommutativitātes pierādījums

Pēc definīcijas a → × b → = i → j → k → a x a y a z b x b y b z un b → × a → = i → j → k → b x b y b z a x a y a z . Un, ja tiek apmainītas divas matricas rindas, tad matricas determinanta vērtībai jāmainās uz pretējo, tāpēc a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , kas un pierāda vektora reizinājuma antikomutativitāti.

Vektorprodukts — piemēri un risinājumi

Vairumā gadījumu ir trīs veidu uzdevumi.

Pirmā veida uzdevumos parasti tiek norādīti divu vektoru garumi un leņķis starp tiem, bet jums ir jāatrod krustojuma garums. Šajā gadījumā izmantojiet šādu formulu c → = a → b → sin ∠ a → , b → .

1. piemērs

Atrodiet vektoru a → un b → šķērsreizinājuma garumu, ja zināms a → = 3 , b → = 5 , ∠ a → , b → = π 4.

Lēmums

Izmantojot vektoru a → un b → vektora reizinājuma garuma definīciju, mēs atrisinām šo uzdevumu: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Atbilde: 15 2 2 .

Otrā tipa uzdevumiem ir saistība ar vektoru koordinātām, tie satur vektora reizinājumu, tā garumu utt. tiek meklēti caur zināmajām doto vektoru koordinātām a → = (a x ; a y ; a z) un b → = (b x ; b y ; b z) .

Šāda veida uzdevumiem varat atrisināt daudzas uzdevumu iespējas. Piemēram, nevis vektoru a → un b → koordinātas, bet to izvērsumus formas koordinātu vektoros b → = b x i → + b y j → + b z k → un c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , vai vektorus a → un b → var norādīt ar to koordinātām. sākuma un beigu punkti.

Apsveriet šādus piemērus.

2. piemērs

Taisnstūra koordinātu sistēmā ir uzstādīti divi vektori a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Atrodiet to vektorproduktu.

Lēmums

Saskaņā ar otro definīciju mēs atrodam divu vektoru vektoru reizinājumu dotās koordinātēs: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k → .

Ja vektora reizinājumu rakstām caur matricas determinantu, tad šī piemēra risinājums ir šāds: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Atbilde: a → × b → = - 2 i → - 2 j → - 2 k → .

3. piemērs

Atrast vektoru i → - j → un i → + j → + k → krustreizinājuma garumu, kur i → , j → , k → - taisnstūra Dekarta koordinātu sistēmas orts.

Lēmums

Vispirms atradīsim dotā vektora reizinājuma i → - j → × i → + j → + k → koordinātes dotajā taisnstūra koordinātu sistēmā.

Ir zināms, ka vektoriem i → - j → un i → + j → + k → ir attiecīgi koordinātas (1 ; - 1 ; 0) un (1 ; 1 ; 1). Atrodiet vektora reizinājuma garumu, izmantojot matricas determinantu, tad mums ir i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Tāpēc vektora reizinājumam i → - j → × i → + j → + k → ir koordinātes (- 1 ; - 1 ; 2) dotajā koordinātu sistēmā.

Vektora reizinājuma garumu atrodam pēc formulas (skat. sadaļu par vektora garuma atrašanu): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Atbilde: i → - j → × i → + j → + k → = 6 . .

4. piemērs

Trīs punktu A (1 , 0 , 1) , B (0 , 2 , 3) ​​, C (1 , 4 , 2) koordinātas ir norādītas taisnstūrveida Dekarta koordinātu sistēmā. Atrodiet kādu vektoru, kas ir perpendikulārs A B → un A C → vienlaikus.

Lēmums

Vektoriem A B → un A C → ir attiecīgi šādas koordinātas (- 1 ; 2 ; 2) un (0 ; 4 ; 1). Atrodot vektoru A B → un A C → vektorreizinājumu, ir skaidrs, ka tas pēc definīcijas ir perpendikulārs vektors gan A B →, gan A C → , tas ir, tas ir mūsu problēmas risinājums. Atrodiet to A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Atbilde: - 6 i → + j → - 4 k → . ir viens no perpendikulārajiem vektoriem.

Trešā tipa problēmas ir vērstas uz vektoru vektoru reizinājuma īpašību izmantošanu. Pēc kuras piemērošanas mēs iegūsim dotās problēmas risinājumu.

5. piemērs

Vektori a → un b → ir perpendikulāri, un to garumi ir attiecīgi 3 un 4. Atrodiet šķērsreizinājuma garumu 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Lēmums

Pēc vektora reizinājuma sadalījuma īpašības mēs varam uzrakstīt 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Pēc asociativitātes īpašības mēs izņemam skaitliskos koeficientus aiz vektora reizinājuma zīmes pēdējā izteiksmē: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Vektoru reizinājumi a → × a → un b → × b → ir vienādi ar 0, jo a → × a → = a → a → sin 0 = 0 un b → × b → = b → b → sin 0 = 0, tad 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

No vektora reizinājuma antikomutativitātes izriet - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Izmantojot vektora reizinājuma īpašības, iegūstam vienādību 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Pēc nosacījuma vektori a → un b → ir perpendikulāri, tas ir, leņķis starp tiem ir vienāds ar π 2 . Tagad atliek tikai aizstāt atrastās vērtības attiecīgajās formulās: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

Atbilde: 3 a → - b → × a → - 2 b → = 60 .

Vektoru krustreizinājuma garums pēc definīcijas ir a → × b → = a → · b → · sin ∠ a → , b → . Tā kā jau ir zināms (no skolas kursa), ka trijstūra laukums ir vienāds ar pusi no tā divu malu garumu reizinājuma, kas reizināts ar leņķa sinusu starp šīm malām. Tāpēc vektora reizinājuma garums ir vienāds ar paralelograma laukumu - dubultotu trīsstūri, proti, malu reizinājumu vektoru a → un b → formā, kas atdalīti no viena punkta ar sinusu. leņķa starp tiem sin ∠ a → , b → .

Šī ir vektora reizinājuma ģeometriskā nozīme.

Vektora reizinājuma fiziskā nozīme

Mehānikā, vienā no fizikas nozarēm, pateicoties vektora reizinājumam, jūs varat noteikt spēka momentu attiecībā pret telpas punktu.

3. definīcija

Zem spēka momenta F → , kas pielikts punktam B , attiecībā pret punktu A mēs sapratīsim šādu vektoru reizinājumu A B → × F → .

Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter

Leņķis starp vektoriem

Lai mēs ieviestu divu vektoru krustreizinājuma jēdzienu, vispirms ir jārisina tāds jēdziens kā leņķis starp šiem vektoriem.

Doti mums divi vektori $\overline(α)$ un $\overline(β)$. Ņemsim kādu punktu $O$ telpā un noliksim malā vektorus $\overline(α)=\overline(OA)$ un $\overline(β)=\overline(OB)$, tad leņķi $AOB. $ tiks saukts par leņķi starp šiem vektoriem (1. att.).

Apzīmējums: $∠(\overline(α),\overline(β))$

Vektoru krustreizinājuma jēdziens un atrašanas formula

1. definīcija

Divu vektoru vektorreizinājums ir vektors, kas ir perpendikulārs abiem dotajiem vektoriem, un tā garums būs vienāds ar šo vektoru garumu reizinājumu ar leņķa sinusu starp šiem vektoriem, un šim vektoram ar diviem sākotnējiem vektoriem ir vienāds orientāciju kā Dekarta koordinātu sistēmu.

Apzīmējums: $\overline(α)х\overline(β)$.

Matemātiski tas izskatās šādi:

1. $|\overline(α)x\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)x\overline(β)⊥\overline(α)$, $\overline(α)x\overline(β)⊥\overline(β)$
3. $(\overline(α)x\overline(β),\overline(α),\overline(β))$ un $(\overline(i),\overline(j),\overline(k))$ ir vienādi orientēts (2. att.)

Acīmredzot vektoru ārējais reizinājums būs vienāds ar nulles vektoru divos gadījumos:

1. Ja viena vai abu vektoru garums ir nulle.
2. Ja leņķis starp šiem vektoriem ir vienāds ar $180^\circ$ vai $0^\circ$ (jo šajā gadījumā sinuss ir vienāds ar nulli).

Lai skaidri redzētu, kā tiek atrasts vektoru krustojums, apsveriet šādus risinājumu piemērus.

1. piemērs

Atrodiet vektora $\overline(δ)$ garumu, kas būs vektoru krustreizinājuma rezultāts ar koordinātām $\overline(α)=(0,4,0)$ un $\overline(β) =(3,0,0 )$.

Lēmums.

Attēlosim šos vektorus Dekarta koordinātu telpā (3. att.):

3. attēls. Vektori Dekarta koordinātu telpā. Autors24 - studentu darbu tiešsaistes apmaiņa

Mēs redzam, ka šie vektori atrodas attiecīgi uz $Ox$ un $Oy$ asīm. Tāpēc leņķis starp tiem būs vienāds ar $90^\circ$. Atradīsim šo vektoru garumus:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

Pēc tam ar 1. definīciju mēs iegūstam moduli $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

Atbilde: $ 12 $.

Šķērsreizinājuma aprēķins pēc vektoru koordinātām

Definīcija 1 uzreiz norāda uz veidu, kā atrast krustenisko reizinājumu diviem vektoriem. Tā kā vektoram papildus vērtībai ir arī virziens, to nav iespējams atrast, izmantojot tikai skalāro vērtību. Bet bez tam ir vēl viens veids, kā atrast mums dotos vektorus, izmantojot koordinātas.

Doti mums vektori $\overline(α)$ un $\overline(β)$, kuriem būs attiecīgi koordinātes $(α_1,α_2,α_3)$ un $(β_1,β_2,β_3)$. Tad šķērsprodukta vektoru (proti, tā koordinātas) var atrast pēc šādas formulas:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

Pretējā gadījumā, paplašinot determinantu, mēs iegūstam šādas koordinātas

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3, α_1 β_2-α_2 β_1)$

2. piemērs

Atrodiet kolineāro vektoru $\overline(α)$ un $\overline(β)$ krustreizinājuma vektoru ar koordinātām $(0,3,3)$ un $(-1,2,6)$.

Lēmums.

Izmantosim iepriekš minēto formulu. gūt

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18) -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$

Atbilde: $(12,-3,3)$.

Vektoru krustreizinājuma īpašības

Patvaļīgi sajauktiem trīs vektoriem $\overline(α)$, $\overline(β)$ un $\overline(γ)$, kā arī $r∈R$ ir spēkā šādas īpašības:

3. piemērs

Atrodiet paralelograma laukumu, kura virsotnēm ir koordinātas $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ un $(3,8,0) $.

Lēmums.

Vispirms uzzīmējiet šo paralelogramu koordinātu telpā (5. att.):

5. attēls. Paralēlogramma koordinātu telpā. Autors24 - studentu darbu tiešsaistes apmaiņa

Mēs redzam, ka šī paralelograma abas malas ir konstruētas, izmantojot kolineārus vektorus ar koordinātām $\overline(α)=(3,0,0)$ un $\overline(β)=(0,8,0)$. Izmantojot ceturto īpašību, mēs iegūstam:

$S=|\overline(α)x\overline(β)|$

Atrodiet vektoru $\overline(α)х\overline(β)$:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

sekojoši

$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$

Acīmredzot krustreizinājuma gadījumā svarīga ir vektoru ņemšanas secība, turklāt

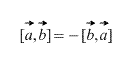
Turklāt tieši no definīcijas izriet, ka jebkuram skalāram faktoram k (skaitlim) ir taisnība:

Kolineāro vektoru šķērsreizinājums ir vienāds ar nulles vektoru. Turklāt divu vektoru krustojums ir nulle tad un tikai tad, ja tie ir kolineāri. (Ja viens no tiem ir nulles vektors, jāatceras, ka nulles vektors pēc definīcijas ir kolineārs jebkuram vektoram).

Vektora produktam ir sadales īpašums, tas ir

Krusta reizinājuma izteiksme vektoru koordinātu izteiksmē.

Doti divi vektori

(kā atrast vektora koordinātas pēc tā sākuma un beigu koordinātām - skatiet rakstu Vektoru punktu reizinājums, rindkopa Punktu reizinājuma alternatīva definīcija vai divu vektoru punktveida reizinājuma aprēķināšana pēc to koordinātām.)

Kāpēc jums ir nepieciešams vektorprodukts?

Šķērsreizinājumu var izmantot daudzos veidos, piemēram, kā jau rakstīts iepriekš, aprēķinot divu vektoru krustojumu, var noskaidrot, vai tie ir kolineāri.

Vai arī to var izmantot kā veidu, kā aprēķināt paralelograma laukumu, kas veidots no šiem vektoriem. Pamatojoties uz definīciju, iegūtā vektora garums ir šī paralelograma laukums.

Arī elektrībā un magnētismā pastāv ļoti daudz pielietojumu.

Tiešsaistes vektorprodukta kalkulators.

Lai, izmantojot šo kalkulatoru, atrastu divu vektoru skalāro reizinājumu, pirmajā rindā ir jāievada pirmā vektora koordinātas, bet otrajā - otrā vektora koordinātas. Vektoru koordinātas var aprēķināt no to sākuma un beigu koordinātām (skatiet rakstu Vektoru punktu reizinājums , vienums Alternatīva punktu reizinājuma definīcija vai divu vektoru punktu reizinājuma aprēķināšana, ņemot vērā to koordinātas.)