Matricas vektorreizinājums. Kā atrast vektoru krustojumu

Punktu produkta īpašības

Vektoru punktu reizinājums, definīcija, īpašības

Lineāras operācijas ar vektoriem.

Vektori, pamatjēdzieni, definīcijas, lineāras darbības uz tiem

Vektors plaknē ir sakārtots tā punktu pāris, savukārt pirmo punktu sauc par vektora sākumu, bet otro par beigām.

Divus vektorus sauc par vienādiem, ja tie ir vienādi un vienādi.

Vektorus, kas atrodas uz vienas līnijas, sauc par kopvirziena, ja tie ir līdzvirzienā ar kādu no tā paša vektora, kas neatrodas uz šīs līnijas.

Vektorus, kas atrodas uz vienas taisnes vai paralēlām līnijām, sauc par kolineāriem, un kolineārus, bet ne līdzvirzienus, sauc par pretēji vērstiem.

Vektorus, kas atrodas uz perpendikulārām līnijām, sauc par ortogonāliem.

Definīcija 5.4. summa a+b vektori a un b sauc par vektoru, kas nāk no vektora sākuma a līdz vektora beigām b , ja vektora sākums b sakrīt ar vektora beigām a .

Definīcija 5.5. atšķirība a - b vektori a un b šādu vektoru sauc ar , kas kopā ar vektoru b dod vektoru a .

Definīcija 5.6. strādātk a vektors a uz numuru k sauc par vektoru b , kolineārs vektors a , kura modulis ir vienāds ar | k||a |, un virziens, kas ir tāds pats kā virziens a plkst k>0 un pretēji a plkst k<0.

Vektora reizināšanas ar skaitli īpašības:

1. īpašums. k(a+b ) = k a+ k b.

2. īpašums. (k+m)a = k a+ m a.

3. īpašums. k(m a) = (km)a .

Sekas. Ja vektori, kas nav nulle a un b ir kolineāri, tad ir skaitlis k, kas b= k a.

Divu nulles vektoru skalārais reizinājums a un b sauc par skaitli (skalāru), kas vienāds ar šo vektoru garumu un starp tiem esošā leņķa φ kosinusu reizinājumu. Skalāro reizinājumu var izteikt dažādos veidos, piemēram, kā ab, a · b, (a , b), (a · b). Tātad punktveida produkts ir:

a · b = |a| · | b| cos φ

Ja vismaz viens no vektoriem ir vienāds ar nulli, tad skalārais reizinājums ir vienāds ar nulli.

Permutācijas īpašums: a · b = b · a(skalārais reizinājums nemainās no faktoru permutācijas);

izplatīšanas īpašums: a · ( b · c) = (a · b) · c(rezultāts nav atkarīgs no reizināšanas kārtības);

Kombinācijas īpašība (attiecībā pret skalāro koeficientu): (λ a) · b = λ ( a · b).

Ortogonalitātes (perpendikularitātes) īpašība: ja vektors a un b kas nav nulle, tad to punktu reizinājums ir nulle tikai tad, ja šie vektori ir ortogonāli (perpendikulāri viens otram) a ┴ b;

Kvadrātveida īpašums: a · a = a 2 = |a| 2 (vektora skalārais reizinājums ar sevi ir vienāds ar tā moduļa kvadrātu);

Ja vektoru koordinātas a=(x 1 , y 1 , z 1 ) un b=(x 2 , y 2 , z 2 ), tad skalārais reizinājums ir a · b= x 1 x 2 + y 1 y 2 + z 1 z 2 .

Vektoru turēšanas vektori. Definīcija: divu vektoru vektorreizinājums, un to saprot kā vektoru, kuram:

Modulis ir vienāds ar paralelograma laukumu, kas veidots uz šiem vektoriem, t.i. , kur ir leņķis starp vektoriem un

Šis vektors ir perpendikulārs reizinātajiem vektoriem, t.i.

Ja vektori nav kolineāri, tad tie veido taisnu vektoru trīskāršu.

Krusta produkta īpašības:

1. Mainot faktoru secību, vektorreizinājums maina savu zīmi uz pretējo, saglabājot moduli, t.i.

2 .Vektoru kvadrāts ir vienāds ar nulles vektoru, t.i.

3 .Skalāro koeficientu var izņemt no vektora reizinājuma zīmes, t.i.

4 .Jebkuriem trim vektoriem vienādība

5 .Nepieciešams un pietiekams nosacījums divu vektoru kolinearitātei un:

Šis tiešsaistes kalkulators aprēķina vektoru krustojumu. Tiek sniegts detalizēts risinājums. Lai aprēķinātu vektoru krustojumu, šūnās ievadiet vektoru koordinātas un noklikšķiniet uz "Aprēķināt".

×

Brīdinājums

Vai dzēst visas šūnas?

Aizvērt Notīrīt

Datu ievades instrukcija. Cipari tiek ievadīti kā veseli skaitļi (piemēri: 487, 5, -7623 utt.), decimālskaitļi (piemēram, 67., 102,54 utt.) vai daļskaitļi. Daļa jāievada formā a/b, kur a un b (b>0) ir veseli vai decimālskaitļi. Piemēri 45/5, 6,6/76,4, -7/6,7 utt.

Vektoru krustreizinājums

Pirms turpināt definēt vektoru vektoru reizinājumu, apsveriet jēdzienus sakārtots vektoru trīskāršs, kreisais vektoru trīskāršs, labais vektoru trīskāršs.

Definīcija 1. Tiek izsaukti trīs vektori pasūtīts trīskāršs(vai trīskāršs), ja norādīts, kurš no šiem vektoriem ir pirmais, kurš otrais un kurš trešais.

Ierakstīšana CBA- nozīmē - pirmais ir vektors c, otrais ir vektors b un trešais ir vektors a.

Definīcija 2. Nekopplanāru vektoru trīskāršs abc sauc par labo (kreiso), ja, reducējot līdz kopējam sākumam, šie vektori ir sakārtoti tā, ka atrodas attiecīgi labās (kreisās) rokas lielie, nesaliektie rādītājpirksti un vidējie pirksti.

2. definīciju var formulēt citā veidā.

Definīcija 2. Nekopplanāru vektoru trīskāršs abc tiek saukts par labo (kreiso), ja, reducējot līdz kopējai izcelsmei, vektoru c kas atrodas vektoru noteiktās plaknes otrā pusē a un b, no kurienes īsākais pagrieziens a uz b veic pretēji pulksteņrādītāja virzienam (pulksteņrādītāja virzienā).

Vektoru trio abc attēlā parādīts. 1 ir pareizs un trīskāršs abc attēlā parādīts. 2 ir palicis.

Ja divi vektoru trīskārši ir pa labi vai pa kreisi, tad tiek uzskatīts, ka tiem ir vienāda orientācija. Pretējā gadījumā tiek teikts, ka tie ir pretējas orientācijas.

Definīcija 3. Dekarta vai afīna koordinātu sistēmu sauc par labo (kreiso), ja trīs bāzes vektori veido labo (kreiso) trīskāršu.

Skaidrības labad turpmāk aplūkosim tikai labās puses koordinātu sistēmas.

4. definīcija. vektormāksla vektors a uz vektoru b sauc par vektoru ar, kas apzīmēts ar simbolu c=[ab] (vai c=[a, b] vai c=a×b) un kas atbilst šādām trim prasībām:

• vektora garums ar ir vienāds ar vektoru garumu reizinājumu a un b līdz leņķa sinusam φ starp viņiem:

|c|=|[ab]|=|a||b|sinφ;

(1)

• vektors ar ortogonāli katram no vektoriem a un b;
• vektors c vērsta tā, ka trīs abc ir pareizi.

Vektoru krustproduktam ir šādas īpašības:

• [ab]=−[ba] (antipermutability faktori);
• [(λa)b]=λ [ab] (saderība attiecībā pret skaitlisko faktoru);
• [(a+b)c]=[ac]+[bc] (izplatīšana attiecībā pret vektoru summu);
• [aa]=0 jebkuram vektoram a.

Vektoru krustojuma ģeometriskās īpašības

1. teorēma. Lai divi vektori būtu kolineāri, ir nepieciešams un pietiekami, lai to vektoru reizinājums būtu vienāds ar nulli.

Pierādījums. Nepieciešamība. Ļaujiet vektoriem a un b kolineārs. Tad leņķis starp tiem ir 0 vai 180° un sinφ=grēks180=grēks 0=0. Tāpēc, ņemot vērā izteiksmi (1), vektora garums c vienāds ar nulli. Tad c nulles vektors.

Atbilstība. Ļaujiet vektoru krustreizinājumam a un b nav uz nulli: [ ab]=0. Pierādīsim, ka vektori a un b kolineārs. Ja vismaz viens no vektoriem a un b nulle, tad šie vektori ir kolineāri (jo nulles vektoram ir nenoteikts virziens un to var uzskatīt par kolineāru jebkuram vektoram).

Ja abi vektori a un b nav nulle, tad | a|>0, |b|>0. Pēc tam no [ ab]=0 un no (1) izriet, ka sinφ=0. Līdz ar to vektori a un b kolineārs.

Teorēma ir pierādīta.

2. teorēma. Vektora reizinājuma garums (modulis) [ ab] ir vienāds ar laukumu S paralelograms, kas veidots uz vektoriem, kas reducēti līdz kopējam sākumam a un b.

Pierādījums. Kā zināms, paralelograma laukums ir vienāds ar šī paralelograma blakus esošo malu un starp tām esošā leņķa sinusa reizinājumu. Sekojoši:

Tad šo vektoru krustojumam ir šāda forma:

Paplašinot determinantu virs pirmās rindas elementiem, iegūstam vektora dekompozīcijas a × b pamats i, j, k, kas ir līdzvērtīga formulai (3).

3. teorēmas pierādījums. Sastādi visus iespējamos bāzes vektoru pārus i, j, k un aprēķina to vektorproduktu. Jāņem vērā, ka bāzes vektori ir savstarpēji ortogonāli, veido taisnu trīskāršu un tiem ir garuma vienība (citiem vārdiem sakot, mēs varam pieņemt, ka i={1, 0, 0}, j={0, 1, 0}, k=(0, 0, 1)). Tad mums ir:

No pēdējās vienādības un attiecībām (4) mēs iegūstam:

Sastādiet 3×3 matricu, kuras pirmā rinda ir bāzes vektori i, j, k, un pārējās rindas ir aizpildītas ar vektoru elementiem a un b:

Tādējādi vektoru krustojuma rezultāts a un b būs vektors:

.

2. piemērs. Atrodiet vektoru šķērsreizinājumu [ ab], kur vektors a attēlots ar diviem punktiem. Vektora a sākuma punkts: , vektora beigu punkts a: , vektors b ir forma .

Risinājums. Pārvietojiet pirmo vektoru uz sākumpunktu. Lai to izdarītu, no attiecīgajām beigu punkta koordinātām atņemiet sākuma punkta koordinātas:

Mēs aprēķinām šīs matricas determinantu, izvēršot to pirmajā rindā. Šo aprēķinu rezultātā iegūstam vektoru vektorreizinājumu a un b.

Definīcija. Vektora a un vektora b vektorreizinājums ir vektors, kas apzīmēts ar simbolu [«, b] (vai l x b), tā ka 1) vektora [a, b] garums ir vienāds ar (p, kur y ir leņķis starp vektoriem a un b ( 31);2) vektors [a, b) ir perpendikulārs vektoriem a un b, t.i. perpendikulāri šo vektoru plaknei; 3) vektors [a, b] ir vērsts tā, ka no šī vektora gala ir redzams, ka īsākais pagrieziens no a uz b notiek pretēji pulksteņrādītāja virzienam (32. att.). Rīsi. 32 31. att. Citiem vārdiem sakot, vektori a, b un [а, b) veido vektoru labo trīskāršu, t.i. atrodas kā labās rokas īkšķis, rādītājpirksts un vidējais pirksts. Ja vektori a un b ir kolineāri, pieņemsim, ka [a, b] = 0. Pēc definīcijas vektora reizinājuma garums ir skaitliski vienāds ar uz reizinātajiem vektoriem uzbūvētā paralelograma (33. att.) laukumu Sa a un b kā sānos: 6.1 . Vektora reizinājuma īpašības 1. Vektora reizinājums ir vienāds ar nulles vektoru tad un tikai tad, ja vismaz viens no reizinātajiem vektoriem ir nulle vai kad šie vektori ir kolineāri (ja vektori a un b ir kolineāri, tad leņķis starp tiem ir 0 vai 7r). To ir viegli iegūt no tā, ka Ja uzskatām nulles vektoru kolinārs jebkuram vektoram, tad vektoru a un b kolinaritātes nosacījumu var izteikt šādi 2. Vektora reizinājums ir antikomutatīvs, t.i., vienmēr. Patiešām, vektori (a, b) un ir vienāda garuma un ir kolineāri. Šo vektoru virzieni ir pretēji, jo no vektora [a, b] gala būs redzams īsākais pagrieziens no a uz b pretēji pulksteņrādītāja virzienam, bet no vektora [b, a] gala - pulksteņrādītāja virzienam (att. 34). 3. Vektora reizinājumam ir sadalījuma īpašība attiecībā uz saskaitīšanu 4. Skaitlisko faktoru A var izņemt no vektora reizinājuma zīmes 6.2. Vektoru reizinājums pēc koordinātām Ļaujiet vektoriem a un b dot to koordinātām bāzē. Izmantojot vektora reizinājuma sadalījuma īpašību, mēs atrodam vektoru vektoru reizinājumu, ko dod koordinātas. Jaukts darbs. Izrakstīsim koordinātu ortu vektorreizinājumus (35. att.): Tāpēc vektoru a un b vektorreizinājumam no formulas (3) iegūstam šādu izteiksmes determinantu pār 1. rindas elementiem, iegūstam ( 4). Piemēri. 1. Atrodiet uz vektoriem veidota paralelograma laukumu Atrodiet trīsstūra laukumu (36. attēls). Ir skaidrs, ka trijstūra JSC laukums b "d ir vienāds ar pusi no paralelograma O AC B laukuma S. Aprēķinot vektoru reizinājumu (a, b | vektoriem a \u003d OA un b \u003d b \u003d ob ), iegūstam (a, b), c) = [a, |b, c)) vispārējā gadījumā nav patiess. Piemēram, a = ss j mums ir § 7. Vektoru jauktais reizinājums. trīs vektori a, b un c.Vektorus a un 1> reizina vektoriski.Rezultātā iegūstam vektoru [a,1>].Reizinām to skalāri ar vektoru c:(k b),c Skaitlis ( [a, b], e) sauc par vektoru a, b. c jaukto reizinājumu un apzīmē ar simbolu (a, 1), e) 7.1. Jauktā reizinājuma ģeometriskā nozīme Noliksim malā vektori a, b un no vispārīgā punkta O (37. att.) Ja visi četri punkti O, A, B, C atrodas vienā plaknē ( vektorus a, b un c šajā gadījumā sauc par koplanāriem), tad jauktais. reizinājums ([a, b], c) = 0. Tas izriet no fakta, ka vektors [a, b| ir perpendikulārs plaknei, kurā atrodas vektori a un 1 ", un līdz ar to vektors c. / Ja t punkti O, A, B, C neatrodas vienā plaknē (vektori a, b un c nav vienāplaknē), uz malām OA, OB un OS veidosim paralēlskaldni (att. 38.a) Pēc krustreizinājuma definīcijas mums ir (a,b) = So c, kur So ir paralelograma OADB laukums, un c ir vienības vektors, kas ir perpendikulārs vektoriem a un b un tāds, ka trīskāršs a , b, c ir pareizi, t.i. vektori a, b un c atrodas attiecīgi kā labās rokas īkšķis, rādītājpirksts un vidējais pirksts (38. att. b). Reizinot abas pēdējās vienādības daļas labajā skalārā ar vektoru c, iegūstam, ka vektoru reizinājums ar koordinātām. Jaukts darbs. Skaitlis rc c ir vienāds ar konstruētā paralēlskaldņa augstumu h, kas ņemts ar “+” zīmi, ja leņķis starp vektoriem c un c ir akūts (trīskāršais a, b, c ir taisns), un ar zīmi “ -” ja leņķis ir neass (trīskāršais a, b, c - pa kreisi), lai Tādējādi vektoru a, b un c jauktais reizinājums ir vienāds ar paralēlskaldņa tilpumu V, kas uzbūvēts uz šiem vektoriem kā uz malām. ja trīskāršs a, b, c ir pa labi, un -V, ja trīskāršs a , b, c - pa kreisi. Pamatojoties uz jauktā reizinājuma ģeometrisko nozīmi, varam secināt, ka reizinot vienādus vektorus a, b un c jebkurā citā secībā, vienmēr iegūsim vai nu +7, vai -K. Zīme pro- Fig. 38 atsauce būs atkarīga tikai no tā, kuru tripletu veido reizinātie vektori – pa labi vai pa kreisi. Ja vektori a, b, c veido taisnu trīskāršu, tad arī trīskārši b, c, a un c, a, b būs pareizi. Tajā pašā laikā visi trīs tripleti b, a, c; a, c, b un c, b, a - pa kreisi. Tādējādi (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b , a). Vēlreiz uzsveram, ka vektoru jauktais reizinājums ir vienāds ar nulli tad un tikai tad, ja reizinātie vektori a, b, c ir koplanāri: (a, b, c ir koplanāri) 7.2. Jaukts reizinājums koordinātēs Ļaujiet vektoriem a, b, c dot pēc to koordinātām bāzē i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Atradīsim izteiksmi viņu jauktajam produktam (a, b, c). Mums ir jaukts vektoru reizinājums, kas dots pēc to koordinātām bāzē i, J, k, vienāds ar trešās kārtas determinantu, kura līnijas attiecīgi sastāv no reizinātā pirmās, otrās un trešās koordinātām. vektori. Nepieciešamo un pietiekamo nosacījumu vektoru a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) komplanaritātei var uzrakstīt šādā formā. z, ar2 y2 -2 =0. Uz Piemērs. Pārbaudiet, vai vektori v = (7,4,6), b = (2, 1,1), c = (19, II, 17) ir vienā plaknē. Apskatāmie vektori būs koplanāri vai nekoplanāri, atkarībā no tā, vai determinants ir vienāds ar nulli vai nē Paplašinot to pirmās rindas elementu izteiksmē, iegūstam 7.3. Dubultā krusta reizinājums Dubultā krusta reizinājums [a, [b, c]] ir vektors, kas ir perpendikulārs vektoriem a un [b, c]. Tāpēc tas atrodas vektoru b un c plaknē un var tikt paplašināts šajos vektoros. Var parādīt, ka formula [a, [!>, c]] = b(a, e) - c(a, b) ir derīga. Uzdevumi 1. Trīs vektori AB = c, W? = o un CA = b kalpo kā trijstūra malas. Izsakiet ar a, b un c vektorus, kas sakrīt ar trijstūra mediānām AM, DN, CP. 2. Kāds nosacījums jāsavieno starp vektoriem p un q, lai vektors p + q sadalītu leņķi starp tiem uz pusēm? Tiek pieņemts, ka visi trīs vektori ir saistīti ar kopīgu izcelsmi. 3. Aprēķināt uz vektoriem a = 5p + 2q un b = p - 3q uzbūvētā paralelograma diagonāļu garumu, ja zināms, ka |p| = 2v/2, |q| = 3 H-(p7ci) = f. 4. Apzīmējot ar a un b romba malas, kas iziet no kopīgas virsotnes, pierādiet, ka romba diagonāles ir savstarpēji perpendikulāras. 5. Aprēķiniet vektoru a = 4i + 7j + 3k un b = 31 - 5j + k punktu reizinājumu. 6. Atrodiet vienību vektoru a0 paralēli vektoram a = (6, 7, -6). 7. Atrodiet vektora a = l+ j- kHa vektora b = 21 - j - 3k projekciju. 8. Atrast kosinusu leņķim starp vektoriem IS "w, ja A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Atrodiet vienības vektoru p°, kas vienlaikus ir perpendikulārs vektoram a = (3, 6, 8) un x asij. 10. Aprēķiniet leņķa sinusu starp paralēlās diagonāles, kas uzbūvētas uz vektoriem a = 2i+J-k, b=i-3j + k kā uz malām. Aprēķināt uz vektoriem a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k uzbūvētā paralēlskaldņa augstumu h, ja par pamatu ņem paralelogramu, kas uzbūvēts uz vektoriem a un I). Atbildes

Acīmredzot krustreizinājuma gadījumā svarīga ir vektoru ņemšanas secība, turklāt

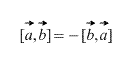
Turklāt tieši no definīcijas izriet, ka jebkuram skalāram faktoram k (skaitlim) ir taisnība:

Kolineāro vektoru šķērsreizinājums ir vienāds ar nulles vektoru. Turklāt divu vektoru krustojums ir nulle tad un tikai tad, ja tie ir kolineāri. (Ja viens no tiem ir nulles vektors, jāatceras, ka nulles vektors pēc definīcijas ir kolineārs jebkuram vektoram).

Vektora produktam ir sadales īpašums, tas ir

Krusta reizinājuma izteiksme vektoru koordinātu izteiksmē.

Doti divi vektori

(kā atrast vektora koordinātas pēc tā sākuma un beigu koordinātām - skatiet rakstu Vektoru punktu reizinājums, rindkopa Punktu reizinājuma alternatīva definīcija vai divu vektoru punktveida reizinājuma aprēķināšana pēc to koordinātām.)

Kāpēc jums ir nepieciešams vektorprodukts?

Šķērsreizinājumu var izmantot daudzos veidos, piemēram, kā jau rakstīts iepriekš, aprēķinot divu vektoru krustojumu, var noskaidrot, vai tie ir kolineāri.

Vai arī to var izmantot kā veidu, kā aprēķināt paralelograma laukumu, kas veidots no šiem vektoriem. Pamatojoties uz definīciju, iegūtā vektora garums ir šī paralelograma laukums.

Tiešsaistes vektorprodukta kalkulators.

Lai, izmantojot šo kalkulatoru, atrastu divu vektoru skalāro reizinājumu, pirmajā rindā ir jāievada pirmā vektora koordinātas, bet otrajā - otrā vektora koordinātas. Vektoru koordinātas var aprēķināt no to sākuma un beigu koordinātām (skatiet rakstu Vektoru punktu reizinājums , vienums Alternatīva punktu reizinājuma definīcija vai divu vektoru punktu reizinājuma aprēķināšana, ņemot vērā to koordinātas.)

Definīcija. Vektora a (reizinātāja) vektora reizinājums ar vektoru (reizinātāju), kas tam nav kolineārs, ir trešais vektors c (reizinātājs), kas tiek konstruēts šādi:

1) tā modulis ir skaitliski vienāds ar paralelograma laukumu attēlā. 155), veidots uz vektoriem, t.i., tas ir vienāds ar virzienu, kas ir perpendikulārs minētā paralelograma plaknei;

3) šajā gadījumā tiek izvēlēts vektora c virziens (no diviem iespējamiem), lai vektori c veidotu labās puses sistēmu (§ 110).

Apzīmējums: vai

Papildinājums definīcijai. Ja vektori ir kolineāri, tad, uzskatot figūru par (nosacīti) paralelogramu, ir dabiski piešķirt nulles laukumu. Tāpēc kolineāro vektoru vektorreizinājums tiek uzskatīts par vienādu ar nulles vektoru.

Tā kā nulles vektoram var piešķirt jebkuru virzienu, šī vienošanās nav pretrunā ar definīcijas 2. un 3. punktu.

1. piezīme. Terminā "vektora reizinājums" pirmais vārds norāda, ka darbības rezultāts ir vektors (pretēji skalārajai reizinājumam; sal. § 104, 1. piezīme).

Piemērs 1. Atrodiet vektoru reizinājumu, kurā atrodas labās koordinātu sistēmas galvenie vektori (156. att.).

1. Tā kā galveno vektoru garumi ir vienādi ar mēroga vienību, tad paralelograma laukums (kvadrāts) skaitliski ir vienāds ar vienu. Tādējādi vektora reizinājuma modulis ir vienāds ar vienu.

2. Tā kā perpendikulārs plaknei ir ass, vēlamā vektora reizinājums ir vektors, kas ir kolineārs vektoram k; un tā kā abiem ir modulis 1, tad vajadzīgais šķērsreizinājums ir vai nu k, vai -k.

3. No šiem diviem iespējamiem vektoriem jāizvēlas pirmais, jo vektori k veido labo sistēmu (un vektori veido kreiso sistēmu).

2. piemērs. Atrodiet krustojumu

Lēmums. Tāpat kā 1. piemērā, mēs secinām, ka vektors ir vai nu k, vai -k. Bet tagad mums ir jāizvēlas -k, jo vektori veido pareizo sistēmu (un vektori veido kreiso). Tātad,

3. piemērs Vektoru garums ir attiecīgi 80 un 50 cm, un tie veido 30° leņķi. Ņemot metru par garuma vienību, atrodiet vektora reizinājuma a garumu

Lēmums. Uz vektoriem veidota paralelograma laukums ir vienāds ar Vēlamā vektora reizinājuma garums ir vienāds ar

Piemērs 4. Atrodiet to pašu vektoru šķērsreizinājuma garumu, par garuma vienību ņemot centimetru.

Lēmums. Tā kā uz vektoriem veidotā paralelograma laukums ir vienāds ar vektora reizinājuma garumu ir 2000 cm, t.i.

Salīdzinot 3. un 4. piemēru, redzams, ka vektora garums ir atkarīgs ne tikai no faktoru garumiem, bet arī no garuma vienības izvēles.

Vektora reizinājuma fiziskā nozīme. No daudzajiem fiziskajiem lielumiem, ko attēlo vektora reizinājums, mēs ņemsim vērā tikai spēka momentu.

Spēka pielikšanas punktu apzīmēsim A. Spēka momentu attiecībā pret punktu O sauc par vektorreizinājumu. Tā kā šī vektora reizinājuma modulis skaitliski ir vienāds ar paralelograma laukumu (157. att.), momenta modulis ir vienāds ar pamatnes reizinājumu ar augstumu, t.i., spēku, kas reizināts ar attālumu no punkta O līdz taisnei, pa kuru darbojas spēks.

Mehānikā ir pierādīts, ka stingra ķermeņa līdzsvaram ir nepieciešams, lai ne tikai vektoru summa, kas atspoguļo ķermenim pieliktos spēkus, bet arī spēku momentu summa būtu vienāda ar nulli. Gadījumā, ja visi spēki ir paralēli vienai un tai pašai plaknei, momentus attēlojošo vektoru saskaitīšanu var aizstāt ar to moduļu saskaitīšanu un atņemšanu. Bet patvaļīgiem spēku virzieniem šāda nomaiņa nav iespējama. Saskaņā ar to krustreizinājums ir precīzi definēts kā vektors, nevis kā skaitlis.