Produkti vektorial i një matrice. Si të gjendet prodhimi kryq i vektorëve

Karakteristikat e produktit me pika

Produkti me pika i vektorëve, përkufizimi, vetitë

Veprime lineare në vektorë.

Vektorët, konceptet bazë, përkufizimet, veprimet lineare mbi to

Një vektor në një plan është një çift i renditur i pikave të tij, ndërsa pika e parë quhet fillimi, dhe e dyta fundi - i vektorit.

Dy vektorë quhen të barabartë nëse janë të barabartë dhe bashkëdrejtues.

Vektorët që shtrihen në të njëjtën linjë quhen bashkëdrejtues nëse janë bashkëdrejtues me disa vektorë të njëjtë që nuk shtrihen në këtë vijë.

Vektorët që shtrihen në të njëjtën drejtëz ose në drejtëza paralele quhen kolinearë, dhe kolinearë, por jo bashkëdrejtues quhen me drejtim të kundërt.

Vektorët që shtrihen në drejtëza pingule quhen ortogonale.

Përkufizimi 5.4. shuma a+b vektorët a dhe b quhet vektori që vjen nga fillimi i vektorit a deri në fund të vektorit b , nëse fillimi i vektorit b përkon me fundin e vektorit a .

Përkufizimi 5.5. dallimi a - b vektorët a dhe b një vektor i tillë quhet Me , i cili së bashku me vektorin b jep një vektor a .

Përkufizimi 5.6. punak a vektoriale a për numër k i quajtur vektor b , vektor kolinear a , i cili ka modul të barabartë me | k||a |, dhe një drejtim që është i njëjtë me drejtimin a në k>0 dhe e kundërta a në k<0.

Vetitë e shumëzimit të një vektori me një numër:

Prona 1. k(a+b ) = k a+ k b.

Prona 2. (k+m)a = k a+ m a.

Prona 3. k(m a) = (km)a .

Pasoja. Nëse vektorë jozero a dhe b janë kolineare, atëherë ka një numër k, çfarë b= k a.

Produkti skalar i dy vektorëve jozero a dhe b quhet numër (skalar) i barabartë me prodhimin e gjatësive të këtyre vektorëve dhe kosinusit të këndit φ ndërmjet tyre. Produkti skalar mund të shprehet në mënyra të ndryshme, për shembull, si ab, a · b, (a , b), (a · b). Pra, produkti me pika është:

a · b = |a| · | b| cos φ

Nëse të paktën njëri prej vektorëve është i barabartë me zero, atëherë produkti skalar është i barabartë me zero.

Vetia e ndërrimit: a · b = b · a(produkti skalar nuk ndryshon nga ndërrimi i faktorëve);

prona e shpërndarjes: a · ( b · c) = (a · b) · c(rezultati nuk varet nga rendi i shumëzimit);

Vetia e kombinimit (në lidhje me faktorin skalar): (λ a) · b = λ ( a · b).

Vetia e ortogonalitetit (perpendikularitetit): nëse vektori a dhe b jo zero, atëherë produkti i tyre me pika është zero vetëm kur këta vektorë janë ortogonalë (pingulë me njëri-tjetrin) a ┴ b;

Prona katrore: a · a = a 2 = |a| 2 (produkti skalar i një vektori me vetveten është i barabartë me katrorin e modulit të tij);

Nëse koordinatat e vektorëve a=(x 1 , y 1 , z 1 ) dhe b=(x 2 , y 2 , z 2 ), atëherë produkti skalar është a · b= x 1 x 2 + y 1 y 2 + z 1 z 2 .

Vektorët mbajtës të vektorit. Përkufizimi: Produkti vektorial i dy vektorëve dhe kuptohet si një vektor për të cilin:

Moduli është i barabartë me sipërfaqen e paralelogramit të ndërtuar mbi këta vektorë, d.m.th. , ku është këndi ndërmjet vektorëve dhe

Ky vektor është pingul me vektorët e shumëzuar, d.m.th.

Nëse vektorët janë jokolinearë, atëherë ata formojnë një treshe drejtë vektorësh.

Karakteristikat e produkteve të kryqëzuara:

1. Kur ndërrohet radha e faktorëve, prodhimi vektorial ndryshon shenjën e tij në të kundërt, duke ruajtur modulin, d.m.th.

2 .Katrori i vektorit është i barabartë me zero-vektor, d.m.th.

3 .Faktori skalar mund të nxirret nga shenja e produktit vektor, d.m.th.

4 .Për çdo tre vektorë, barazia

5 .Kusht i domosdoshëm dhe i mjaftueshëm për kolinearitetin e dy vektorëve dhe :

Ky kalkulator në internet llogarit produktin kryq të vektorëve. Jepet një zgjidhje e detajuar. Për të llogaritur prodhimin e tërthortë të vektorëve, futni koordinatat e vektorëve në qeliza dhe klikoni në "Llogarit".

×

Paralajmërim

Të pastrohen të gjitha qelizat?

Mbylle Pastro

Udhëzim për futjen e të dhënave. Numrat futen si numra të plotë (shembuj: 487, 5, -7623, etj.), numra dhjetorë (p.sh. 67., 102.54, etj.) ose thyesa. Thyesa duhet të shtypet në formën a/b, ku a dhe b (b>0) janë numra të plotë ose dhjetorë. Shembujt 45/5, 6.6/76.4, -7/6.7, etj.

Prodhimi i kryqëzuar i vektorëve

Para se të vazhdoni me përkufizimin e produktit vektorial të vektorëve, merrni parasysh konceptet trefishi i renditur i vektorëve, trefishi i majtë i vektorëve, trefishi i djathtë i vektorëve.

Përkufizim 1. Quhen tre vektorë porositi trefish(ose trefish) nëse tregohet se cili nga këta vektorë është i pari, cili i dyti dhe cili i treti.

Regjistrimi cba- do të thotë - i pari është një vektor c, i dyti është vektori b dhe i treti është vektori a.

Përkufizim 2. Një trefish i vektorëve joplanarë abc quhet djathtas (majtas) nëse, kur reduktohet në një fillim të përbashkët, këta vektorë janë të renditur ashtu siç janë vendosur përkatësisht gishti tregues i madh, i palakuar dhe i mesëm i dorës së djathtë (të majtë).

Përkufizimi 2 mund të formulohet në një mënyrë tjetër.

Përkufizim 2. Një trefish i vektorëve joplanarë abc quhet djathtas (majtas) nëse, kur reduktohet në një origjinë të përbashkët, vektori c të vendosura në anën tjetër të rrafshit të përcaktuar nga vektorët a dhe b, prej nga vjen kthesa më e shkurtër a te b kryhet në drejtim të kundërt (në drejtim të akrepave të orës).

Treshe vektoriale abc treguar në fig. 1 është e drejtë dhe e trefishtë abc treguar në fig. 2 ka mbetur.

Nëse dy treshe vektorësh janë djathtas ose majtas, atëherë thuhet se kanë të njëjtin orientim. Ndryshe, thuhet se janë me orientim të kundërt.

Përkufizimi 3. Një sistem koordinativ kartezian ose afin quhet djathtas (majtas) nëse tre vektorët bazë formojnë një treshe djathtas (majtas).

Për saktësi, në atë që vijon do të shqyrtojmë vetëm sistemet e koordinatave të djathta.

Përkufizimi 4. arti vektor vektoriale a për vektor b i quajtur vektor Me, e shënuar me simbolin c=[ab] (ose c=[a,b], ose c=a×b) dhe plotëson tre kërkesat e mëposhtme:

• gjatësi vektoriale Meështë e barabartë me prodhimin e gjatësive të vektorëve a dhe b në sinusin e këndit φ mes tyre:

|c|=|[ab]|=|a||b|sinφ;

(1)

• vektoriale Me ortogonal me secilin nga vektorët a dhe b;
• vektoriale c drejtuar në mënyrë që të tre abc ka te drejte.

Produkti kryq i vektorëve ka këto veti:

• [ab]=−[ba] (antipermutabiliteti faktorë);
• [(λa)b]=λ [ab] (pajtueshmërinë në lidhje me faktorin numerik);
• [(a+b)c]=[ac]+[bc] (shpërndarja në lidhje me shumën e vektorëve);
• [aa]=0 për çdo vektor a.

Vetitë gjeometrike të prodhimit kryq të vektorëve

Teorema 1. Që dy vektorë të jenë kolinear, është e nevojshme dhe e mjaftueshme që produkti i tyre vektor të jetë i barabartë me zero.

Dëshmi. Nevoja. Lërini vektorët a dhe b kolineare. Atëherë këndi ndërmjet tyre është 0 ose 180° dhe sinφ=mëkat180=mëkat 0=0. Prandaj, duke marrë parasysh shprehjen (1), gjatësinë e vektorit c barazohet me zero. Pastaj c vektor zero.

Përshtatshmëria. Lëreni prodhimin kryq të vektorëve a dhe b navigoni në zero: [ ab]=0. Le të vërtetojmë se vektorët a dhe b kolineare. Nëse të paktën një nga vektorët a dhe b zero, atëherë këta vektorë janë kolinearë (sepse vektori zero ka një drejtim të pacaktuar dhe mund të konsiderohet kolinear me çdo vektor).

Nëse të dy vektorët a dhe b jozero, atëherë | a|>0, |b|>0. Pastaj nga [ ab]=0 dhe nga (1) rrjedh se sinφ=0. Prandaj vektorët a dhe b kolineare.

Teorema është vërtetuar.

Teorema 2. Gjatësia (moduli) i produktit të vektorit [ ab] është e barabartë me sipërfaqen S paralelogrami i ndërtuar mbi vektorë të reduktuar në një origjinë të përbashkët a dhe b.

Dëshmi. Siç e dini, sipërfaqja e një paralelogrami është e barabartë me produktin e anëve ngjitur të këtij paralelogrami dhe sinusit të këndit midis tyre. Rrjedhimisht:

Atëherë prodhimi kryq i këtyre vektorëve ka formën:

Duke e zgjeruar përcaktorin mbi elementët e rreshtit të parë, marrim zbërthimin e vektorit a×b bazë i, j, k, e cila është e barabartë me formulën (3).

Vërtetimi i teoremës 3. Hartoni të gjitha çiftet e mundshme të vektorëve bazë i, j, k dhe llogarit produktin e tyre vektor. Duhet të merret parasysh se vektorët bazë janë reciprokisht ortogonalë, formojnë një treshe të drejtë dhe kanë gjatësi njësi (me fjalë të tjera, mund të supozojmë se i={1, 0, 0}, j={0, 1, 0}, k=(0, 0, 1)). Atëherë kemi:

Nga barazia dhe marrëdhëniet e fundit (4), marrim:

Hartoni një matricë 3×3, rreshti i parë i së cilës janë vektorët bazë i, j, k, dhe rreshtat e mbetur mbushen me elemente vektorësh a dhe b:

Kështu, rezultati i prodhimit të kryqëzuar të vektorëve a dhe b do të jetë një vektor:

.

Shembulli 2. Gjeni prodhimin kryq të vektorëve [ ab], ku vektori a përfaqësohet nga dy pika. Pika e fillimit të vektorit a: , pika fundore e vektorit a: , vektor b ka formën .

Zgjidhje.Lëvizni vektorin e parë në origjinë. Për ta bërë këtë, zbritni nga koordinatat përkatëse të pikës fundore koordinatat e pikës fillestare:

Ne llogarisim përcaktorin e kësaj matrice duke e zgjeruar në rreshtin e parë. Si rezultat i këtyre llogaritjeve, marrim produktin vektorial të vektorëve a dhe b.

Përkufizimi. Produkti vektorial i një vektori a dhe vektori b është një vektor i shënuar me simbolin [«, b] (ose l x b), i tillë që 1) gjatësia e vektorit [a, b] është e barabartë me (p, ku y është këndi ndërmjet vektorëve a dhe b (31); 2) vektori [a, b) është pingul me vektorët a dhe b, d.m.th. pingul me rrafshin e këtyre vektorëve; 3) vektori [a, b] drejtohet në atë mënyrë që nga fundi i këtij vektori të shihet rrotullimi më i shkurtër nga a në b në drejtim të kundërt të akrepave të orës (Fig. 32). Oriz. 32 Fig.31 Me fjalë të tjera, vektorët a, b dhe [а, b) formojnë treshen e djathtë të vektorëve, d.m.th. të vendosura si gishti i madh, tregues dhe i mesëm i dorës së djathtë. Nëse vektorët a dhe b janë kolinearë, do të supozojmë se [a, b] = 0. Sipas përkufizimit, gjatësia e prodhimit të vektorit është numerikisht e barabartë me sipërfaqen Sa të paralelogramit (Fig. 33) të ndërtuar mbi vektorët e shumëzuar a dhe b si në anët: 6.1 . Vetitë e një produkti vektorial 1. Një produkt vektorial është i barabartë me një vektor zero nëse dhe vetëm nëse të paktën njëri nga vektorët e shumëzuar është zero ose kur këta vektorë janë kolinear (nëse vektorët a dhe b janë kolinear, atëherë këndi ndërmjet tyre është ose 0 ose 7r). Kjo është e lehtë për t'u përftuar nga fakti se nëse marrim kolinsarin zero të vektorit për çdo vektor, atëherë kushti për kolinaritetin e vektorëve a dhe b mund të shprehet si më poshtë 2. Produkti vektorial është antikomutativ, d.m.th. gjithmonë. Në të vërtetë, vektorët (a, b) dhe kanë të njëjtën gjatësi dhe janë kolinearë. Drejtimet e këtyre vektorëve janë të kundërta, pasi nga fundi i vektorit [a, b] do të shihet kthesa më e shkurtër nga a në b që ndodh në drejtim të kundërt të akrepave të orës, dhe nga fundi i vektorit [b, a] - në drejtim të akrepave të orës (Fig. 34). 3. Produkti vektor ka një veti shpërndarëse në lidhje me mbledhjen 4. Faktori numerik A mund të hiqet nga shenja e prodhimit vektorial 6.2. Prodhimi vektorial i vektorëve të dhënë me koordinata Le të jepen vektorët a dhe b me koordinatat e tyre në bazë. Duke përdorur vetinë e shpërndarjes së produktit vektor, gjejmë produktin vektorial të vektorëve të dhënë nga koordinatat. Punë e përzier. Le të shkruajmë prodhimet vektoriale të orteve të koordinatave (Fig. 35): Prandaj, për produktin vektorial të vektorëve a dhe b, marrim nga formula (3) shprehjen e mëposhtme përcaktor mbi elementët e rreshtit të parë, marrim ( 4). Shembuj. 1. Gjeni sipërfaqen e një paralelogrami të ndërtuar mbi vektorë Gjeni sipërfaqen e trekëndëshit (Fig. 36). Është e qartë se sipërfaqja b "d e trekëndëshit JSC është e barabartë me gjysmën e sipërfaqes S të paralelogramit O AC B. Llogaritja e produktit të vektorit (a, b | e vektorëve a \u003d OA dhe b \u003d b \u003d ob ), fitojmë (a, b), c) = [a, |b, c)) nuk është e vërtetë në rastin e përgjithshëm. Për shembull, për a = ss j kemi § 7. Prodhimi i përzier i vektorëve Le të kemi tre vektorë a, b dhe c. Shumëzojmë vektorët a dhe 1> në mënyrë vektoriale. Si rezultat, marrim vektorin [a, 1>]. E shumëzojmë atë në shkallëzim me vektorin c: (k b), c. Numri ( [a, b], e) quhet prodhim i përzier i vektorëve a, b.c dhe shënohet me simbolin (a, 1), e) 7.1 Kuptimi gjeometrik i prodhimit të përzier Le të lëmë mënjanë vektorët a, b dhe nga pika e përgjithshme O (Fig. 37) Nëse të katër pikat O, A, B, C shtrihen në të njëjtin rrafsh ( vektorët a, b dhe c quhen në këtë rast koplanarë), atëherë të përzierat prodhimi ([a, b], c) = 0. Kjo rrjedh nga fakti se vektori [a, b| është pingul me rrafshin në të cilin shtrihen vektorët a dhe 1 ", dhe kështu vektori c. / Nëse t pikat O, A, B, C nuk shtrihen në të njëjtin rrafsh (vektorët a, b dhe c janë jokoplanarë), ne do të ndërtojmë një paralelipiped në skajet OA, OB dhe OS (Fig. 38 a). Me përcaktimin e prodhimit kryq, kemi (a,b) = Pra c, ku Pra është sipërfaqja e paralelogramit OADB, dhe c është një vektor njësi pingul me vektorët a dhe b dhe i tillë që trefishi a , b, c ka të drejtë, d.m.th. vektorët a, b dhe c janë të vendosur përkatësisht si gishti i madh, tregues dhe i mesëm i dorës së djathtë (Fig. 38 b). Duke shumëzuar të dyja pjesët e barazisë së fundit në skalarin e djathtë me vektorin c, marrim se prodhimi vektorial i vektorëve të dhënë nga koordinatat. Punë e përzier. Numri rc c është i barabartë me lartësinë h të paralelopipedit të ndërtuar, i marrë me shenjën "+" nëse këndi midis vektorëve c dhe c është i mprehtë (trefishi a, b, c është i drejtë), dhe me shenjën " -” nëse këndi është i mpirë (trefishi a, b, c - majtas), kështu që prodhimi i përzier i vektorëve a, b dhe c është i barabartë me vëllimin V të paralelopipedit të ndërtuar mbi këta vektorë si në skaje. nëse trefishi a, b, c është i drejtë, dhe -V nëse trefishi a , b, c - majtas. Bazuar në kuptimin gjeometrik të produktit të përzier, mund të konkludojmë se duke shumëzuar të njëjtët vektorë a, b dhe c në çdo renditje tjetër, gjithmonë do të marrim ose +7 ose -K. Shenja e pro- Fig. 38 referenca do të varet vetëm nga cila treshe formojnë vektorët e shumëzuar - djathtas ose majtas. Nëse vektorët a, b, c formojnë një treshe të drejtë, atëherë trefishat b, c, a dhe c, a, b do të jenë gjithashtu të drejta. Në të njëjtën kohë, të tre trinjakët b, a, c; a, c, b dhe c, b, a - majtas. Kështu, (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b, a). Theksojmë edhe një herë se prodhimi i përzier i vektorëve është i barabartë me zero nëse dhe vetëm nëse vektorët e shumëzuar a, b, c janë koplanarë: (a, b, c janë koplanarë) 7.2. Produkti i përzier në koordinata Le të jepen vektorët a, b, c me koordinatat e tyre në bazën i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Le të gjejmë një shprehje për produktin e tyre të përzier (a, b, c). Kemi një prodhim të përzier vektorësh të dhënë nga koordinatat e tyre në bazën i, J, k, të barabartë me përcaktorin e rendit të tretë, vijat e të cilit përbëhen përkatësisht nga koordinatat e së parës, të dytë dhe të tretë të shumëzuar. vektorët. Kushti i nevojshëm dhe i mjaftueshëm për komplanaritetin e vektorëve a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) mund të shkruhet në formën e mëposhtme z, ar2 y2 -2 =0. Shembull Uz. Kontrolloni nëse vektorët v = (7,4,6), b = (2, 1,1), c = (19, II, 17) janë bashkëplanarë. Vektoret ne shqyrtim do te jene koplanare ose jokoplanare, ne varesi te faktit nese percaktorja eshte e barabarte me zero apo jo.Duke e zgjeruar ate persa i perket elementeve te rreshtit te pare fitojme 7.3. Produkt kryq i dyfishtë Prodhimi kryq i dyfishtë [a, [b, c]] është një vektor pingul me vektorët a dhe [b, c]. Prandaj, ai shtrihet në rrafshin e vektorëve b dhe c dhe mund të zgjerohet në këta vektorë. Mund të tregohet se formula [a, [!>, c]] = b(a, e) - c(a, b) është e vlefshme. Ushtrimet 1. Tre vektorë AB = c, W? = o dhe CA = b shërbejnë si brinjë të trekëndëshit. Shprehni në terma a, b dhe c vektorët që përkojnë me medianat AM, DN, CP të trekëndëshit. 2. Çfarë kushti duhet të lidhet ndërmjet vektorëve p dhe q në mënyrë që vektori p + q ta ndajë këndin ndërmjet tyre përgjysmë? Supozohet se të tre vektorët janë të lidhur me një origjinë të përbashkët. 3. Njehsoni gjatësinë e diagonaleve të paralelogramit të ndërtuar mbi vektorët a = 5p + 2q dhe b = p - 3q, nëse dihet se |p| = 2v/2, |q| = 3 H-(p7ci) = f. 4. Duke shënuar me a dhe b brinjët e rombit që dalin nga një kulm i përbashkët, provoni se diagonalet e rombit janë reciproke pingule. 5. Njehsoni prodhimin pikësor të vektorëve a = 4i + 7j + 3k dhe b = 31 - 5j + k. 6. Gjeni vektorin njësi a0 paralel me vektorin a = (6, 7, -6). 7. Gjeni projeksionin e vektorit a = l+ j- kHa vektor b = 21 - j - 3k. 8. Gjeni kosinusin e këndit ndërmjet vektorëve IS "w, nëse A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Gjeni një vektor njësi p° që është njëkohësisht pingul me vektorin a = (3, 6, 8) dhe boshtin x. 10. Njehsoni sinusin e këndit ndërmjet diagonaleve të paralelofamit të ndërtuar mbi vektorët a = 2i+J-k, b=i-3j + k si në brinjë. Njehsoni lartësinë h të paralelopipedit të ndërtuar mbi vektorët a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k, nëse për bazë merret paralelogrami i ndërtuar mbi vektorët a dhe I). Përgjigjet

Natyrisht, në rastin e një prodhimi kryq, rendi në të cilin janë marrë vektorët ka rëndësi, për më tepër,

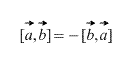
Gjithashtu, drejtpërdrejt nga përkufizimi rrjedh se për çdo faktor skalar k (numër) është e vërtetë:

Produkti kryq i vektorëve kolinearë është i barabartë me vektorin zero. Për më tepër, prodhimi kryq i dy vektorëve është zero nëse dhe vetëm nëse janë kolinear. (Në rast se njëri prej tyre është një vektor zero, është e nevojshme të mbani mend se vektori zero është kolinear me çdo vektor sipas definicionit).

Produkti vektor ka pronë distributive, kjo eshte

Shprehja e prodhimit kryq në terma të koordinatave të vektorëve.

Le të jepen dy vektorë

(si të gjejmë koordinatat e një vektori sipas koordinatave të fillimit dhe mbarimit të tij - shih artikullin Produkti me pika i vektorëve, paragrafi Përkufizimi alternativ i produktit me pika ose llogaritja e produktit me pika të dy vektorëve të dhënë nga koordinatat e tyre.)

Pse keni nevojë për një produkt vektori?

Ka shumë mënyra për të përdorur produktin kryq, për shembull, siç është shkruar tashmë më lart, duke llogaritur prodhimin kryq të dy vektorëve, mund të zbuloni nëse ato janë kolineare.

Ose mund të përdoret si një mënyrë për të llogaritur sipërfaqen e një paralelogrami të ndërtuar nga këta vektorë. Bazuar në përkufizimin, gjatësia e vektorit që rezulton është zona e këtij paralelogrami.

Llogaritësi në internet i produktit vektor.

Për të gjetur produktin skalar të dy vektorëve duke përdorur këtë kalkulator, duhet të vendosni koordinatat e vektorit të parë në rreshtin e parë, dhe vektorin e dytë në të dytën. Koordinatat e vektorëve mund të llogariten nga koordinatat e tyre fillestare dhe fundore (shih artikullin Produkti me pika i vektorëve , artikull Një përkufizim alternativ i produktit me pika, ose llogaritja e produktit pika të dy vektorëve duke pasur parasysh koordinatat e tyre.)

Përkufizimi. Prodhimi vektorial i një vektori a (shumëzues) nga një vektor (shumësues) që nuk është kolinear me të është vektori i tretë c (produkti), i cili është ndërtuar si më poshtë:

1) moduli i tij është numerikisht i barabartë me sipërfaqen e paralelogramit në fig. 155), i ndërtuar mbi vektorë, d.m.th., është i barabartë me drejtimin pingul me rrafshin e paralelogramit të përmendur;

3) në këtë rast, drejtimi i vektorit c zgjidhet (nga dy të mundshëm) në mënyrë që vektorët c të formojnë një sistem të djathtë (§ 110).

Emërtimi: ose

Shtesë e përkufizimit. Nëse vektorët janë kolinear, atëherë duke e konsideruar figurën si një paralelogram (me kusht), është e natyrshme të caktohet zona zero. Prandaj, produkti vektorial i vektorëve kolinearë konsiderohet i barabartë me vektorin zero.

Meqenëse vektorit null mund t'i caktohet çdo drejtim, kjo konventë nuk bie në kundërshtim me pikat 2 dhe 3 të përkufizimit.

Vërejtje 1. Në termin "produkt vektorial", fjala e parë tregon se rezultati i një veprimi është një vektor (në krahasim me një produkt skalar; krh. § 104, vërejtja 1).

Shembull 1. Gjeni produktin vektor ku janë vektorët kryesorë të sistemit të koordinatave të duhura (Fig. 156).

1. Meqenëse gjatësitë e vektorëve kryesorë janë të barabartë me njësinë e shkallës, sipërfaqja e paralelogramit (katrorit) është numerikisht e barabartë me një. Prandaj, moduli i produktit vektor është i barabartë me një.

2. Meqenëse pingul me rrafshin është boshti, prodhimi i dëshiruar i vektorit është një vektor kolinear me vektorin k; dhe meqenëse të dyja kanë modulin 1, prodhimi kryq i kërkuar është ose k ose -k.

3. Nga këta dy vektorë të mundshëm, duhet zgjedhur i pari, pasi vektorët k formojnë një sistem të djathtë (dhe vektorët formojnë një të majtë).

Shembulli 2. Gjeni prodhimin kryq

Zgjidhje. Si në shembullin 1, arrijmë në përfundimin se vektori është ose k ose -k. Por tani duhet të zgjedhim -k, pasi vektorët formojnë sistemin e duhur (dhe vektorët formojnë të majtën). Kështu që,

Shembulli 3 Vektorët kanë gjatësi përkatësisht 80 dhe 50 cm dhe formojnë një kënd prej 30°. Duke marrë një metër si njësi gjatësie, gjeni gjatësinë e prodhimit të vektorit a

Zgjidhje. Sipërfaqja e një paralelogrami të ndërtuar mbi vektorë është e barabartë me Gjatësia e produktit të dëshiruar të vektorit është e barabartë me

Shembulli 4. Gjeni gjatësinë e prodhimit kryq të vektorëve të njëjtë, duke marrë një centimetër si njësi gjatësie.

Zgjidhje. Meqenëse sipërfaqja e paralelogramit të ndërtuar mbi vektorë është e barabartë me gjatësinë e produktit të vektorit është 2000 cm, d.m.th.

Krahasimi i shembujve 3 dhe 4 tregon se gjatësia e vektorit varet jo vetëm nga gjatësia e faktorëve, por edhe nga zgjedhja e njësisë së gjatësisë.

Kuptimi fizik i produktit vektor. Nga shumë sasi fizike të përfaqësuara nga produkti vektorial, ne do të marrim parasysh vetëm momentin e forcës.

Le të jetë A pika e aplikimit të forcës. Momenti i forcës në lidhje me pikën O quhet prodhim vektori. Meqenëse moduli i këtij produkti vektorial është numerikisht i barabartë me sipërfaqen e paralelogramit (Fig. 157), moduli i momentit është i barabartë me produktin e bazës me lartësinë, d.m.th., forca e shumëzuar me distancën nga pika O në vijën e drejtë përgjatë së cilës vepron forca.

Në mekanikë, vërtetohet se për ekuilibrin e një trupi të ngurtë është e nevojshme që jo vetëm shuma e vektorëve që përfaqësojnë forcat e aplikuara ndaj trupit, por edhe shuma e momenteve të forcave duhet të jetë e barabartë me zero. Në rastin kur të gjitha forcat janë paralele me të njëjtin rrafsh, mbledhja e vektorëve që përfaqësojnë momentet mund të zëvendësohet me mbledhjen dhe zbritjen e moduleve të tyre. Por për drejtimet arbitrare të forcave, një zëvendësim i tillë është i pamundur. Në përputhje me këtë, prodhimi i kryqëzuar përcaktohet saktësisht si një vektor, dhe jo si një numër.