В този урок ще разгледаме още две операции с вектори: кръстосано произведение на вектории смесено произведение на вектори (незабавна връзка за тези, които имат нужда). Нищо, понякога се случва, че за пълно щастие, освен точково произведение на вектори, необходимо е още и още. Такава е векторната зависимост. Човек може да остане с впечатлението, че навлизаме в джунглата на аналитичната геометрия. Това не е вярно. В този раздел на висшата математика обикновено има малко дърва за огрев, освен може би достатъчно за Пинокио. Всъщност материалът е много общ и прост - едва ли е по-труден от същия скаларно произведение, дори ще има по-малко типични задачи. Основното нещо в аналитичната геометрия, както мнозина ще видят или вече са видели, е ДА НЕ СЕ ГРЕШАТ ИЗЧИСЛЕНИЯТА. Повторете като заклинание и ще бъдете щастливи =)

Ако векторите искрят някъде далеч, като светкавица на хоризонта, няма значение, започнете с урока Вектори за манекениза възстановяване или повторно придобиване на основни знания за векторите. По-подготвените читатели могат да се запознаят с информацията избирателно, опитах се да събера най-пълната колекция от примери, които често се срещат в практическата работа

Какво ще ви направи щастливи? Когато бях малък, можех да жонглирам с две и дори с три топки. Получи се добре. Сега изобщо няма нужда да жонглираме, тъй като ще обмислим само космически вектори, а плоските вектори с две координати ще бъдат пропуснати. Защо? Така се раждат тези действия – векторът и смесеният продукт от вектори са дефинирани и работят в триизмерно пространство. Вече по-лесно!

В тази операция, по същия начин, както при скаларното произведение, два вектора. Нека бъдат нетленни букви.

Самото действие означенопо следния начин: . Има и други опции, но аз съм свикнал да обозначавам кръстосаното произведение на векторите по този начин, в квадратни скоби с кръст.

И то веднага въпрос: ако в точково произведение на векториучастват два вектора и тук два вектора също се умножават, тогава каква е разликата? Ясна разлика, на първо място, в РЕЗУЛТАТА:

Резултатът от скаларното произведение на векторите е ЧИСЛО:

Резултатът от кръстосаното произведение на векторите е ВЕКТОР: , тоест умножаваме векторите и отново получаваме вектор. Затворен клуб. Всъщност оттам идва и името на операцията. В различна образователна литература обозначенията също могат да варират, ще използвам буквата.

Дефиниция на кръстосано произведение

Първо ще има определение със снимка, след това коментари.

Определение: кръстосано произведение неколинеарнивектори, взети в този ред, се нарича ВЕКТОР, дължинакоето е числено равна на площта на успоредника, изграден върху тези вектори; вектор ортогонални на вектори, и е насочен така, че основата да има правилна ориентация:

Анализираме определението по кости, има много интересни неща!

Така че можем да подчертаем следните важни точки:

1) Изходни вектори, обозначени с червени стрелки, по дефиниция не е колинеарен. Ще бъде подходящо да разгледаме случая на колинеарни вектори малко по-късно.

2) Взети вектори в строг ред: – "a" се умножава по "be", а не "бъде" към "а". Резултат от векторно умножениее ВЕКТОР , който е означен в синьо. Ако векторите се умножат в обратен ред, тогава получаваме вектор с еднаква дължина и противоположна посока (червен цвят). Тоест равенството .

3) Сега нека се запознаем с геометричния смисъл на векторното произведение. Това е много важен момент! ДЪЛЖИНАТА на синия вектор (и, следователно, пурпурния вектор) е числено равна на ПЛОЩТА на успоредника, изграден върху векторите. На фигурата този успоредник е оцветен в черно.

Забележка : чертежът е схематичен и, разбира се, номиналната дължина на напречния продукт не е равна на площта на паралелограма.

Спомняме си една от геометричните формули: площта на паралелограма е равна на произведението на съседните страни и синуса на ъгъла между тях. Следователно, въз основа на гореизложеното, формулата за изчисляване на ДЪЛЖИНАТА на векторно произведение е валидна:

Подчертавам, че във формулата говорим за ДЪЛЖИНАТА на вектора, а не за самия вектор. Какъв е практическият смисъл? И смисълът е такъв, че в проблемите на аналитичната геометрия площта на успоредник често се намира чрез концепцията за векторен продукт:

Получаваме втората важна формула. Диагоналът на успоредника (червена пунктирана линия) го разделя на два равни триъгълника. Следователно площта на триъгълник, изграден върху вектори (червено засенчване), може да се намери по формулата:

4) Също толкова важен факт е, че векторът е ортогонален на векторите , т.е . Разбира се, противоположно насоченият вектор (червена стрелка) също е ортогонален на оригиналните вектори.

5) Векторът е насочен така, че базаТо има точноориентация. В урок за преход към нова основаГоворил съм подробно за равнинна ориентация, а сега ще разберем каква е ориентацията на пространството. Ще ти обясня на пръсти дясна ръка. Мислено комбинирайте показалецс вектор и среден пръстс вектор. Безименен пръст и малък пръстнатиснете в дланта си. Като резултат палец- векторният продукт ще изглежда нагоре. Това е дясно ориентираната основа (тя е на фигурата). Сега разменете векторите ( показалец и среден пръст) на някои места в резултат на това палецът ще се обърне и векторният продукт вече ще гледа надолу. Това също е дясно ориентирана основа. Може би имате въпрос: каква основа има лява ориентация? "Присвояване" на същите пръсти лява ръкавектори и вземете лявата основа и лявата пространствена ориентация (в този случай палецът ще бъде разположен в посока на долния вектор). Образно казано, тези основи „извиват” или ориентират пространството в различни посоки. И тази концепция не трябва да се счита за нещо пресилено или абстрактно - например най-обикновеното огледало променя ориентацията на пространството и ако „издърпате отразения обект от огледалото“, тогава като цяло няма да е възможно комбинирайте го с „оригинала“. Между другото, донесете три пръста до огледалото и анализирайте отражението ;-)

... колко е хубаво, че вече знаете за това дясно и ляво ориентиранибази, защото твърденията на някои преподаватели за промяната на ориентацията са ужасни =)

Векторно произведение на колинеарни вектори

Дефиницията е разработена в детайли, остава да разберем какво се случва, когато векторите са колинеарни. Ако векторите са колинеарни, тогава те могат да бъдат поставени на една права линия и нашият успоредник също се „сгъва“ в една права линия. Областта на такива, както казват математиците, изродениуспоредник е нула. Същото следва и от формулата - синус от нула или 180 градуса е равен на нула, което означава, че площта е нула

По този начин, ако , тогава и . Моля, обърнете внимание, че самото кръстосано произведение е равно на нулевия вектор, но на практика това често се пренебрегва и се пише, че също е равно на нула.

Специален случай е векторното произведение на вектор и себе си:

Използвайки кръстосаното произведение, можете да проверите колинеарността на триизмерните вектори и ние също ще анализираме този проблем, наред с други.

За решаване на практически примери може да е необходимо тригонометрична таблицаза да намерите стойностите на синусите от него.

Е, нека запалим огън:

Пример 1

а) Намерете дължината на векторното произведение на векторите, ако

б) Намерете площта на успоредник, изграден върху вектори, ако

Решение: Не, това не е правописна грешка, умишлено направих първоначалните данни в елементите на условието същите. Защото дизайнът на решенията ще бъде различен!

а) Според условието се изисква да се намери дължинавектор (векторен продукт). Съгласно съответната формула:

Отговор:

Тъй като беше зададен въпрос за дължината, тогава в отговора посочваме измерението - единици.

б) Според условието се изисква да се намери квадратуспоредник, построен върху вектори. Площта на този успоредник е числено равна на дължината на напречния продукт:

Отговор:

Моля, имайте предвид, че в отговора за векторното произведение изобщо не се говори, за което бяхме попитани площ на фигурата, съответно размерът е квадратни единици.

Винаги гледаме КАКВО се изисква да се намери от условието и въз основа на това формулираме ясноотговор. Може да изглежда като буквализъм, но сред преподавателите има достатъчно буквалисти и задачата с добри шансове ще бъде върната за преработка. Въпреки че това не е особено напрегната заядка - ако отговорът е грешен, тогава се създава впечатлението, че човекът не разбира прости неща и / или не е разбрал същността на задачата. Този момент винаги трябва да се държи под контрол, решавайки всяка задача по висша математика, а и по други предмети.

Къде отиде голямата буква "ен"? По принцип можеше да се залепи допълнително към разтвора, но за да съкратя записа, не го направих. Надявам се, че всички разбират това и е обозначението на едно и също нещо.

Популярен пример за решение „направи си сам“:

Пример 2

Намерете площта на триъгълник, изграден върху вектори, ако

Формулата за намиране на площта на триъгълник чрез векторния продукт е дадена в коментарите към дефиницията. Решение и отговор в края на урока.

На практика задачата наистина е много често срещана, триъгълниците като цяло могат да бъдат измъчвани.

За да решим други проблеми, имаме нужда от:

Свойства на кръстосаното произведение на вектори

Вече разгледахме някои свойства на векторния продукт, но ще ги включа в този списък.

За произволни вектори и произволно число са верни следните свойства:

1) В други източници на информация този елемент обикновено не се отличава в свойствата, но е много важен от практическа гледна точка. Така че нека бъде.

2) - имотът също е обсъден по-горе, понякога се нарича антикомутативност. С други думи, редът на векторите има значение.

3) - комбинация или асоциативензакони за векторни продукти. Константите лесно се изваждат извън границите на векторното произведение. Наистина, какво правят те там?

4) - разпределение или разпространениезакони за векторни продукти. Няма проблеми и с отварянето на скоби.

Като демонстрация разгледайте кратък пример:

Пример 3

Намерете дали

решение:По условие отново се изисква да се намери дължината на векторното произведение. Нека нарисуваме нашата миниатюра:

(1) Съгласно асоциативните закони изваждаме константите извън границите на векторното произведение.

(2) Изваждаме константата от модула, докато модулът „изяжда“ знака минус. Дължината не може да бъде отрицателна.

(3) Това, което следва, е ясно.

Отговор:

Време е да хвърлим дърва в огъня:

Пример 4

Изчислете площта на триъгълник, изграден върху вектори, ако

Решение: Намерете площта на триъгълник, като използвате формулата . Проблемът е, че самите вектори "ce" и "te" са представени като суми от вектори. Алгоритъмът тук е стандартен и донякъде напомня на примери № 3 и 4 от урока. Точково произведение на вектори. Нека го разделим на три стъпки за по-голяма яснота:

1) На първата стъпка изразяваме векторното произведение чрез векторното произведение, всъщност, изразете вектора чрез вектора. Все още няма дума за дължина!

(1) Заменяме изрази на вектори .

(2) Използвайки законите на разпределението, отваряме скобите според правилото за умножение на полиноми.

(3) Използвайки асоциативните закони, изваждаме всички константи извън векторните продукти. С малко опит действия 2 и 3 могат да се извършват едновременно.

(4) Първият и последният член са равни на нула (нулев вектор) поради приятното свойство . Във втория член използваме свойството антикомутативност на векторното произведение:

(5) Представяме подобни условия.

В резултат на това векторът се оказа изразен чрез вектор, което беше необходимо да се постигне:

2) На втората стъпка намираме дължината на векторния продукт, от който се нуждаем. Това действие е подобно на Пример 3:

3) Намерете площта на необходимия триъгълник:

Стъпки 2-3 от решението могат да бъдат подредени в един ред.

Отговор:

Разглежданият проблем е доста често срещан в тестовете, ето пример за независимо решение:

Пример 5

Намерете дали

Кратко решение и отговор в края на урока. Нека да видим колко внимателни бяхте, когато изучавахте предишните примери ;-)

Напречно произведение на вектори в координати

, дадено в ортонормалната основа, се изразява с формулата:

Формулата е наистина проста: записваме координатните вектори в горния ред на детерминантата, „опаковаме“ координатите на векторите във втория и третия ред и поставяме в строг ред- първо координатите на вектора "ve", след това координатите на вектора "double-ve". Ако векторите трябва да бъдат умножени в различен ред, тогава линиите също трябва да бъдат разменени:

Пример 10

Проверете дали следните пространствени вектори са колинеарни:
а)
б)

Решение: Тестът се основава на едно от твърденията в този урок: ако векторите са колинеарни, тогава тяхното кръстосано произведение е нула (нулев вектор): .

а) Намерете векторното произведение:

Така че векторите не са колинеарни.

б) Намерете векторното произведение:

Отговор: а) не е колинеарен, б)

Тук може би е цялата основна информация за векторното произведение на векторите.

Този раздел няма да е много голям, тъй като има малко проблеми, при които се използва смесеното произведение на вектори. Всъщност всичко ще се основава на дефиницията, геометричното значение и няколко работещи формули.

Смесеното произведение на вектори е произведение на три вектора:

Така се наредиха като влак и чакат, няма търпение да ги изчислят.

Първо отново дефиницията и снимката:

Определение: Смесен продукт некомпланарнивектори, взети в този ред, е наречен обем на паралелепипеда, изграден върху тези вектори, оборудвани със знак "+", ако основата е дясна, и знак "-", ако основата е лява.

Да направим чертежа. Невидимите за нас линии са начертани с пунктирана линия:

Нека се потопим в определението:

2) Взети вектори в определен ред, тоест пермутацията на векторите в продукта, както можете да се досетите, не остава без последствия.

3) Преди да коментирам геометричното значение, ще отбележа очевидния факт: смесеното произведение на векторите е ЧИСЛО: . В образователната литература дизайнът може да е малко по-различен, използвах за обозначаване на смесен продукт чрез и резултата от изчисленията с буквата "pe".

А-приори смесеният продукт е обемът на паралелепипеда, построен върху вектори (фигурата е начертана с червени вектори и черни линии). Тоест числото е равно на обема на дадения паралелепипед.

Забележка : Чертежът е схематичен.

4) Нека не се занимаваме отново с концепцията за ориентацията на основата и пространството. Смисълът на финалната част е, че към обема може да се добави знак минус. С прости думи, смесеният продукт може да бъде отрицателен: .

Формулата за изчисляване на обема на паралелепипед, изграден върху вектори, следва директно от определението.

7.1. Дефиниция на кръстосано произведение

Три некомпланарни вектора a, b и c, взети в посочения ред, образуват дясна тройка, ако от края на третия вектор c най-късият завой от първия вектор a към втория вектор b се вижда обратно на часовниковата стрелка, и наляво, ако е по посока на часовниковата стрелка (виж Фиг. 16).

Векторното произведение на вектор a и вектор b се нарича вектор c, който:

1. Перпендикулярно на векторите a и b, т.е. c ^ a и c ^ b;

2. Има дължина, числено равна на площта на успоредника, построен върху векторите a иbкакто отстрани (виж фиг. 17), т.е.

3. Векторите a , b и c образуват дясна тройка.

Векторното произведение се означава с a x b или [a,b]. От дефиницията на векторно произведение директно следват следните отношения между ортите i, йи к(вижте фиг. 18):

i x j \u003d k, j x k \u003d i, k x i \u003d j.
Нека докажем, например, това i xj \u003d k.

1) k ^ i , k ^ j;

2) |k |=1, но | i x j| = |i | |J| sin(90°)=1;

3) вектори i, j и кобразуват дясна тройка (виж фиг. 16).

7.2. Свойства на кръстосани продукти

1. При пренареждане на факторите векторното произведение променя знака, т.е. и xb \u003d (b xa) (виж Фиг. 19).

Векторите a xb и b xa са колинеарни, имат еднакви модули (площта на паралелограма остава непроменена), но са противоположно насочени (тройки a, b, a xb и a, b, b x a с противоположна ориентация). Това е axb = -(bxa).

2. Векторният продукт има комбинирано свойство по отношение на скаларния фактор, т.е. l ​​(a xb) \u003d (l a) x b \u003d a x (l b).

Нека l >0. Векторът l (a xb) е перпендикулярен на векторите a и b. вектор ( ла) х bсъщо е перпендикулярна на векторите a и b(вектори a, лно лежат в една равнина). Така че векторите л(a xb) и ( ла) х bколинеарен. Очевидно е, че посоките им съвпадат. Имат еднаква дължина:

Ето защо л(a xb)= л a xb. По подобен начин се доказва за л<0.

3. Два ненулеви вектора a и bса колинеарни тогава и само ако тяхното векторно произведение е равно на нулевия вектор, т.е. и ||b<=>и xb \u003d 0.

По-специално, i *i =j *j =k *k =0 .

4. Векторният продукт има разпределително свойство:

(а+б) xs = a xs + b xs .

Приеми без доказателства.

7.3. Изразяване на кръстосано произведение по отношение на координати

Ще използваме векторната таблица с кръстосано произведение i, йи к:

ако посоката на най-късия път от първия вектор до втория съвпада с посоката на стрелката, тогава продуктът е равен на третия вектор, ако не съвпада, третият вектор се взема със знак минус.

Нека два вектора a =a x i +a y й+аз ки b=bx аз+от й+bz к. Нека намерим векторното произведение на тези вектори, като ги умножим като полиноми (според свойствата на векторното произведение):

Получената формула може да бъде написана дори по-кратко:

тъй като дясната страна на равенството (7.1) съответства на разширението на детерминанта от трети ред по отношение на елементите на първия ред.Равенството (7.2) е лесно за запомняне.

7.4. Някои приложения на кръстосаното произведение

Установяване на колинеарност на вектори

Намиране на лицето на успоредник и триъгълник

Според дефиницията на кръстосаното произведение на векторите аи б |a xb | =| а | * |b |sin g , т.е. S par = |a x b |. И следователно D S \u003d 1/2 | a x b |.

Определяне на момента на силата спрямо точка

Нека в точка А е приложена сила F = ABостави О- някаква точка в пространството (виж фиг. 20).

От физиката е известно, че въртящ момент Е спрямо точката Онаречен вектор М,който минава през точката Ои:

1) перпендикулярна на равнината, минаваща през точките О, А, Б;

2) числено равно на произведението на силата и рамото

3) образува дясна тройка с вектори OA и A B .

Следователно M \u003d OA x F.

Намиране на линейната скорост на въртене

Скорост vточка М на твърдо тяло, въртящо се с ъглова скорост wоколо фиксирана ос, се определя от формулата на Ойлер v \u003d w x r, където r \u003d OM, където O е някаква фиксирана точка на оста (виж фиг. 21).

Преди да дадем концепцията за векторно произведение, нека се обърнем към въпроса за ориентацията на подредената тройка от вектори a → , b → , c → в триизмерното пространство.

Като начало нека отделим векторите a → , b → , c → от една точка. Ориентацията на тройката a → , b → , c → е дясна или лява в зависимост от посоката на вектора c → . От посоката, в която е направен най-късият завой от вектора a → към b → от края на вектора c → ще се определи формата на тройката a → , b → , c →.

Ако най-краткото въртене е обратно на часовниковата стрелка, тогава тройката от вектори a → , b → , c → се нарича точноако по часовниковата стрелка - наляво.

След това вземете два неколинеарни вектора a → и b → . Нека тогава отложим векторите A B → = a → и A C → = b → от точката A. Нека построим вектор A D → = c → , който е перпендикулярен едновременно на A B → и A C → . По този начин, когато конструираме вектора A D → = c →, можем да направим две неща, като му дадем една или обратна посока (вижте илюстрацията).

Подреденото трио от вектори a → , b → , c → може да бъде, както разбрахме, дясно или ляво в зависимост от посоката на вектора.

От горното можем да въведем определението за векторен продукт. Тази дефиниция е дадена за два вектора, дефинирани в правоъгълна координатна система на триизмерно пространство.

Определение 1

Векторното произведение на два вектора a → и b → ще наречем такъв вектор, даден в правоъгълна координатна система на триизмерно пространство, така че:

• ако векторите a → и b → са колинеарни, то ще бъде нула;
• той ще бъде перпендикулярен както на вектор a →​​, така и на вектор b → т.е. ∠ a → c → = ∠ b → c → = π 2 ;
• дължината му се определя по формулата: c → = a → b → sin ∠ a → , b → ;
• тройката от вектори a → , b → , c → има същата ориентация като дадената координатна система.

Кръстосаното произведение на вектори a → и b → има следната нотация: a → × b → .

Координати на кръстосани продукти

Тъй като всеки вектор има определени координати в координатната система, е възможно да се въведе второ определение на векторния продукт, което ще ви позволи да намерите неговите координати от дадените координати на векторите.

Определение 2

В правоъгълна координатна система на тримерното пространство векторно произведение на два вектора a → = (a x ; a y ; a z) и b → = (b x ; b y ; b z) наричаме вектора c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , където i → , j → , k → са координатни вектори.

Векторното произведение може да бъде представено като детерминанта на квадратна матрица от трети ред, където първият ред е орта векторите i → , j → , k → , вторият ред съдържа координатите на вектора a → , а третият е координатите на вектора b → в дадена правоъгълна координатна система, тази детерминанта на матрицата изглежда така: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Разгръщайки този детерминант върху елементите на първия ред, получаваме равенството: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = = a → × b → = ( a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Свойства на кръстосани продукти

Известно е, че векторното произведение в координати се представя като детерминанта на матрицата c → = a → × b → = i → j → k → a x a y a z b x b y b z , тогава на основата детерминантни свойства на матрицатаследното векторни свойства на продукта:

1. антикомутативност a → × b → = - b → × a → ;
2. дистрибутивност a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → или a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. асоциативност λ a → × b → = λ a → × b → или a → × (λ b →) = λ a → × b → , където λ е произволно реално число.

Тези свойства нямат сложни доказателства.

Например, можем да докажем свойството антикомутативност на векторен продукт.

Доказателство за антикомутативност

По дефиниция a → × b → = i → j → k → a x a y a z b x b y b z и b → × a → = i → j → k → b x b y b z a x a y a z . И ако два реда на матрицата са разменени, тогава стойността на детерминантата на матрицата трябва да се промени на противоположната, следователно, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , което и доказва антикомутативността на векторното произведение.

Векторен продукт - примери и решения

В повечето случаи има три вида задачи.

В задачите от първия тип обикновено се дават дължините на два вектора и ъгълът между тях, но трябва да намерите дължината на напречното произведение. В този случай използвайте следната формула c → = a → b → sin ∠ a → , b → .

Пример 1

Намерете дължината на кръстосаното произведение на вектори a → и b →, ако е известно a → = 3 , b → = 5 , ∠ a → , b → = π 4.

Решение

Използвайки дефиницията на дължината на векторното произведение на векторите a → и b →, решаваме тази задача: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Отговор: 15 2 2 .

Задачите от втория тип имат връзка с координатите на вектори, съдържат векторно произведение, неговата дължина и др. се търсят по известните координати на дадените вектори a → = (a x; a y; a z) и b → = (b x ; b y ; b z) .

За този тип задачи можете да решите много опции за задачи. Например не координатите на векторите a → и b → , а техните разширения в координатни вектори от формата b → = b x i → + b y j → + b z k → и c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , или векторите a → и b → могат да бъдат дадени чрез координатите на техните начална и крайна точка.

Разгледайте следните примери.

Пример 2

Два вектора са зададени в правоъгълна координатна система a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Намерете тяхното векторно произведение.

Решение

Съгласно втората дефиниция намираме векторното произведение на два вектора в дадени координати: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k → .

Ако напишем векторното произведение чрез детерминанта на матрицата, тогава решението на този пример е както следва: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Отговор: a → × b → = - 2 i → - 2 j → - 2 k → .

Пример 3

Намерете дължината на кръстосаното произведение на вектори i → - j → и i → + j → + k → , където i → , j → , k → - ортове на правоъгълна декартова координатна система.

Решение

Първо, нека намерим координатите на даденото векторно произведение i → - j → × i → + j → + k → в дадената правоъгълна координатна система.

Известно е, че векторите i → - j → и i → + j → + k → имат съответно координати (1 ; - 1 ; 0) и (1 ; 1 ; 1). Намерете дължината на векторното произведение, като използвате детерминанта на матрицата, тогава имаме i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Следователно векторното произведение i → - j → × i → + j → + k → има координати (- 1 ; - 1 ; 2) в дадената координатна система.

Намираме дължината на векторното произведение по формулата (вижте раздела за намиране на дължината на вектора): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

Отговор: i → - j → × i → + j → + k → = 6 . .

Пример 4

Координатите на три точки A (1 , 0 , 1) , B (0 , 2 , 3) ​​​​, C (1 , 4 , 2) са дадени в правоъгълна декартова координатна система. Намерете някакъв вектор, перпендикулярен на A B → и A C → едновременно.

Решение

Векторите A B → и A C → имат съответно следните координати (- 1 ; 2 ; 2) и (0 ; 4 ; 1). След като намерихме векторното произведение на векторите A B → и A C → , очевидно е, че това е перпендикулярен вектор по дефиниция както на A B →, така и на A C → , тоест това е решението на нашата задача. Намерете го A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Отговор: - 6 i → + j → - 4 k → . е един от перпендикулярните вектори.

Задачите от трети тип са фокусирани върху използването на свойствата на векторното произведение на векторите. След прилагането на които ще получим решение на зададения проблем.

Пример 5

Векторите a → и b → са перпендикулярни и техните дължини са съответно 3 и 4. Намерете дължината на напречното произведение 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Решение

Чрез свойството на дистрибутивност на векторното произведение можем да запишем 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Чрез свойството на асоциативността изваждаме числовите коефициенти отвъд знака на векторните произведения в последния израз: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Векторните произведения a → × a → и b → × b → са равни на 0, тъй като a → × a → = a → a → sin 0 = 0 и b → × b → = b → b → sin 0 = 0, тогава 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

От антикомутативността на векторното произведение следва - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Използвайки свойствата на векторното произведение, получаваме равенството 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

По условие векторите a → и b → са перпендикулярни, т.е. ъгълът между тях е равен на π 2 . Сега остава само да замените намерените стойности в съответните формули: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

Отговор: 3 a → - b → × a → - 2 b → = 60 .

Дължината на кръстосаното произведение на векторите по дефиниция е a → × b → = a → · b → · sin ∠ a → , b → . Тъй като вече е известно (от училищния курс), че площта на триъгълник е равна на половината от произведението на дължините на двете му страни, умножено по синуса на ъгъла между тези страни. Следователно дължината на векторния продукт е равна на площта на успоредник - удвоен триъгълник, а именно произведението на страните под формата на вектори a → и b → , отложени от една точка, от синуса на ъгъла между тях sin ∠ a → , b → .

Това е геометричното значение на векторното произведение.

Физическото значение на векторното произведение

В механиката, един от клоновете на физиката, благодарение на векторния продукт, можете да определите момента на сила спрямо точка в пространството.

Определение 3

Под момент на сила F → , приложен към точка B , спрямо точка A ще разбираме следното векторно произведение A B → × F → .

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

Ъгъл между векторите

За да можем да въведем концепцията за кръстосано произведение на два вектора, първо трябва да се справим с такова понятие като ъгъла между тези вектори.

Нека са ни дадени два вектора $\overline(α)$ и $\overline(β)$. Нека вземем някаква точка $O$ в пространството и отделим векторите $\overline(α)=\overline(OA)$ и $\overline(β)=\overline(OB)$ от нея, тогава ъгълът $AOB $ ще се нарича ъгъл между тези вектори (фиг. 1).

Нотация: $∠(\overline(α),\overline(β))$

Понятието кръстосано произведение на вектори и формула за намиране

Определение 1

Векторното произведение на два вектора е вектор, перпендикулярен на двата дадени вектора, и неговата дължина ще бъде равна на произведението на дължините на тези вектори със синуса на ъгъла между тези вектори и този вектор с два начални има същото ориентация като декартова координатна система.

Нотация: $\overline(α)х\overline(β)$.

Математически изглежда така:

1. $|\overline(α)x\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)x\overline(β)⊥\overline(α)$, $\overline(α)x\overline(β)⊥\overline(β)$
3. $(\overline(α)x\overline(β),\overline(α),\overline(β))$ и $(\overline(i),\overline(j),\overline(k))$ са еднакво ориентирани (фиг. 2)

Очевидно външното произведение на векторите ще бъде равно на нулевия вектор в два случая:

1. Ако дължината на единия или двата вектора е нула.
2. Ако ъгълът между тези вектори е равен на $180^\circ$ или $0^\circ$ (защото в този случай синусът е равен на нула).

За да видите ясно как се намира кръстосаното произведение на векторите, разгледайте следните примери за решения.

Пример 1

Намерете дължината на вектора $\overline(δ)$, който ще бъде резултат от кръстосаното произведение на вектори, с координати $\overline(α)=(0,4,0)$ и $\overline(β) =(3,0,0 )$.

Решение.

Нека изобразим тези вектори в декартово координатно пространство (фиг. 3):

Фигура 3. Вектори в декартово координатно пространство. Author24 - онлайн обмен на студентски работи

Виждаме, че тези вектори лежат съответно на осите $Ox$ и $Oy$. Следователно ъгълът между тях ще бъде равен на $90^\circ$. Нека намерим дължините на тези вектори:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

Тогава, по дефиниция 1, получаваме модула $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

Отговор: $12$.

Изчисляване на кръстосаното произведение по координатите на векторите

Дефиниция 1 веднага предполага начин за намиране на кръстосаното произведение за два вектора. Тъй като векторът, освен стойност, има и посока, е невъзможно да се намери само с помощта на скаларна стойност. Но освен него, има друг начин да намерим дадените ни вектори, като използваме координатите.

Нека са ни дадени вектори $\overline(α)$ и $\overline(β)$, които ще имат съответно координати $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$. Тогава векторът на кръстосаното произведение (а именно неговите координати) може да се намери по следната формула:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

В противен случай, разширявайки детерминантата, получаваме следните координати

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

Пример 2

Намерете вектора на кръстосаното произведение на колинеарни вектори $\overline(α)$ и $\overline(β)$ с координати $(0,3,3)$ и $(-1,2,6)$.

Решение.

Нека използваме формулата по-горе. Вземете

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$

Отговор: $(12,-3,3)$.

Свойства на кръстосаното произведение на вектори

За произволни смесени три вектора $\overline(α)$, $\overline(β)$ и $\overline(γ)$, както и $r∈R$, са валидни следните свойства:

Пример 3

Намерете площта на успоредник, чиито върхове имат координати $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0) $.

Решение.

Първо начертайте този успоредник в координатно пространство (фиг. 5):

Фигура 5. Успоредник в координатно пространство. Author24 - онлайн обмен на студентски работи

Виждаме, че двете страни на този паралелограм са конструирани с помощта на колинеарни вектори с координати $\overline(α)=(3,0,0)$ и $\overline(β)=(0,8,0)$. Използвайки четвъртото свойство, получаваме:

$S=|\overline(α)x\overline(β)|$

Намерете вектора $\overline(α)х\overline(β)$:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

Следователно

$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$

Очевидно, в случай на кръстосано произведение, редът, в който се вземат векторите, има значение, освен това,

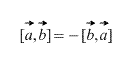
Също така, директно от дефиницията следва, че за всеки скаларен фактор k (число) е вярно следното:

Напречното произведение на колинеарни вектори е равно на нулевия вектор. Освен това кръстосаното произведение на два вектора е нула тогава и само ако те са колинеарни. (В случай, че един от тях е нулев вектор, трябва да запомните, че нулевият вектор е колинеарен на всеки вектор по дефиниция).

Векторният продукт има разпределителна собственост, това е

Изразяването на кръстосаното произведение по отношение на координатите на векторите.

Нека са дадени два вектора

(как да намерите координатите на вектор по координатите на неговото начало и край - вижте статията Точков продукт на вектори, параграф Алтернативна дефиниция на точковия продукт или изчисляване на точковия продукт на два вектора, дадени от техните координати.)

Защо ви е необходим векторен продукт?

Има много начини да използвате кръстосаното произведение, например, както вече беше написано по-горе, като изчислите кръстосаното произведение на два вектора, можете да разберете дали те са колинеарни.

Или може да се използва като начин за изчисляване на площта на успоредник, изграден от тези вектори. Въз основа на определението дължината на получения вектор е площта на този успоредник.

Освен това съществуват огромен брой приложения в електричеството и магнетизма.

Онлайн калкулатор на векторно произведение.

За да намерите скаларното произведение на два вектора с помощта на този калкулатор, трябва да въведете координатите на първия вектор в първия ред по ред, а на втория вектор във втория. Координатите на векторите могат да бъдат изчислени от техните начални и крайни координати (вижте статията Точково произведение на вектори , елемент Алтернативна дефиниция на точково произведение или изчисляване на точково произведение на два вектора, дадени техните координати.)