Finding the derivative of a given function f is called. Derivative of e to the power of x and exponential function

In this lesson, we will learn how to apply formulas and rules of differentiation.

Examples. Find derivatives of functions.

1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Applying the Rule I, formulas 4, 2 and 1. We get:

y'=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.

2. y=3x6 -2x+5. We solve similarly, using the same formulas and the formula 3.

y’=3∙6x 5 -2=18x 5 -2.

Applying the Rule I, formulas 3, 5 And 6 And 1.

Applying the Rule IV, formulas 5 And 1 .

In the fifth example, according to the rule I the derivative of the sum is equal to the sum of the derivatives, and we just found the derivative of the 1st term (example 4 ), therefore, we will find derivatives 2nd And 3rd terms, and for 1st term, we can immediately write the result.

Differentiating 2nd And 3rd terms according to the formula 4 . To do this, we transform the roots of the third and fourth degrees in denominators to powers with negative exponents, and then, according to 4 formula, we find the derivatives of the powers.

Look at this example and the result. Did you catch the pattern? Fine. This means that we have a new formula and can add it to our derivatives table.

Let's solve the sixth example and derive one more formula.

We use the rule IV and formula 4 . We reduce the resulting fractions.

We look at this function and its derivative. You, of course, understood the pattern and are ready to name the formula:

Learning new formulas!

Examples.

1. Find argument increment and function increment y= x2 if the initial value of the argument was 4 , and the new 4,01 .

Solution.

New argument value x \u003d x 0 + Δx. Substitute the data: 4.01=4+Δx, hence the increment of the argument Δх=4.01-4=0.01. The increment of a function, by definition, is equal to the difference between the new and previous values ​​of the function, i.e. Δy \u003d f (x 0 + Δx) - f (x 0). Since we have a function y=x2, That Δу\u003d (x 0 + Δx) 2 - (x 0) 2 \u003d (x 0) 2 + 2x 0 · Δx+(Δx) 2 - (x 0) 2 \u003d 2x 0 · ∆x+(∆x) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Answer: argument increment Δх=0.01; function increment Δу=0,0801.

It was possible to find the function increment in another way: Δy\u003d y (x 0 + Δx) -y (x 0) \u003d y (4.01) -y (4) \u003d 4.01 2 -4 2 \u003d 16.0801-16 \u003d 0.0801.

2. Find the angle of inclination of the tangent to the function graph y=f(x) at the point x 0, If f "(x 0) \u003d 1.

Solution.

The value of the derivative at the point of contact x 0 and is the value of the tangent of the slope of the tangent (the geometric meaning of the derivative). We have: f "(x 0) \u003d tgα \u003d 1 → α \u003d 45 °, because tg45°=1.

Answer: the tangent to the graph of this function forms an angle with the positive direction of the Ox axis, equal to 45°.

3. Derive the formula for the derivative of a function y=xn.

Differentiation is the act of finding the derivative of a function.

When finding derivatives, formulas are used that were derived on the basis of the definition of the derivative, in the same way as we derived the formula for the derivative degree: (x n)" = nx n-1.

Here are the formulas.

Derivative table it will be easier to memorize by pronouncing verbal formulations:

1. The derivative of a constant value is zero.

2. X stroke is equal to one.

3. The constant factor can be taken out of the sign of the derivative.

4. The derivative of a degree is equal to the product of the exponent of this degree by the degree with the same base, but the exponent is one less.

5. The derivative of the root is equal to one divided by two of the same roots.

6. The derivative of unity divided by x is minus one divided by x squared.

7. The derivative of the sine is equal to the cosine.

8. The derivative of cosine is equal to minus sine.

9. The derivative of the tangent is equal to one divided by the square of the cosine.

10. The derivative of the cotangent is minus one divided by the square of the sine.

We teach differentiation rules.

1. The derivative of the algebraic sum is equal to the algebraic sum of the derivative terms.

2. The derivative of the product is equal to the product of the derivative of the first factor by the second plus the product of the first factor by the derivative of the second.

3. The derivative of “y” divided by “ve” is equal to a fraction, in the numerator of which “y is a stroke multiplied by “ve” minus “y, multiplied by a stroke”, and in the denominator - “ve squared”.

4. A special case of the formula 3.

Let's learn together!

Page 1 of 1 1

When solving various problems of geometry, mechanics, physics and other branches of knowledge, it became necessary to use the same analytical process from a given function y=f(x) get a new function called derivative function(or simply derivative) of this function f(x) and are symbolized

The process by which a given function f(x) get a new function f"(x), called differentiation and it consists of the following three steps: 1) we give the argument x increment  x and determine the corresponding increment of the function  y = f(x+ x)-f(x); 2) make up the relation

3) counting x permanent, and  x0, we find
, which is denoted by f"(x), as if emphasizing that the resulting function depends only on the value x, at which we pass to the limit. Definition: Derivative y "=f" (x) given function y=f(x) given x is called the limit of the ratio of the increment of the function to the increment of the argument, provided that the increment of the argument tends to zero, if, of course, this limit exists, i.e. finite. Thus,
, or

Note that if for some value x, for example when x=a, relation
at  x0 does not tend to a finite limit, then in this case we say that the function f(x) at x=a(or at the point x=a) has no derivative or is not differentiable at a point x=a.

2. The geometric meaning of the derivative.

Consider the graph of the function y \u003d f (x), differentiable in the vicinity of the point x 0

f(x)

Let's consider an arbitrary straight line passing through the point of the graph of the function - the point A (x 0, f (x 0)) and intersecting the graph at some point B (x; f (x)). Such a straight line (AB) is called a secant. From ∆ABC: ​​AC = ∆x; BC \u003d ∆y; tgβ=∆y/∆x .

Since AC || Ox, then ALO = BAC = β (as corresponding in parallel). But ALO is the angle of inclination of the secant AB to the positive direction of the Ox axis. Hence, tgβ = k is the slope of the straight line AB.

Now we will decrease ∆x, i.e. ∆x→ 0. In this case, point B will approach point A according to the graph, and the secant AB will rotate. The limiting position of the secant AB at ∆x → 0 will be the straight line (a), called the tangent to the graph of the function y \u003d f (x) at point A.

If we pass to the limit as ∆х → 0 in the equality tgβ =∆y/∆x, then we get
or tg \u003d f "(x 0), since
-angle of inclination of the tangent to the positive direction of the Ox axis
, by definition of a derivative. But tg \u003d k is the slope of the tangent, which means that k \u003d tg \u003d f "(x 0).

So, the geometric meaning of the derivative is as follows:

Derivative of a function at a point x 0 equal to the slope of the tangent to the graph of the function drawn at the point with the abscissa x 0 .

3. Physical meaning of the derivative.

Consider the movement of a point along a straight line. Let the coordinate of a point at any time x(t) be given. It is known (from the course of physics) that the average speed over a period of time is equal to the ratio of the distance traveled during this period of time to the time, i.e.

Vav = ∆x/∆t. Let us pass to the limit in the last equality as ∆t → 0.

lim Vav (t) = (t 0) - instantaneous speed at time t 0, ∆t → 0.

and lim = ∆x/∆t = x "(t 0) (by the definition of a derivative).

So, (t) = x"(t).

The physical meaning of the derivative is as follows: the derivative of the functiony = f(x) at the pointx 0 is the rate of change of the functionf(x) at the pointx 0

The derivative is used in physics to find the speed from a known function of coordinates from time, acceleration from a known function of speed from time.

 (t) \u003d x "(t) - speed,

a(f) = "(t) - acceleration, or

If the law of motion of a material point along a circle is known, then it is possible to find the angular velocity and angular acceleration during rotational motion:

φ = φ(t) - change in angle with time,

ω \u003d φ "(t) - angular velocity,

ε = φ"(t) - angular acceleration, or ε = φ"(t).

If the distribution law for the mass of an inhomogeneous rod is known, then the linear density of the inhomogeneous rod can be found:

m \u003d m (x) - mass,

x  , l - rod length,

p \u003d m "(x) - linear density.

With the help of the derivative, problems from the theory of elasticity and harmonic vibrations are solved. Yes, according to Hooke's law

F = -kx, x – variable coordinate, k – coefficient of elasticity of the spring. Putting ω 2 \u003d k / m, we obtain the differential equation of the spring pendulum x "(t) + ω 2 x (t) \u003d 0,

where ω = √k/√m is the oscillation frequency (l/c), k is the spring rate (H/m).

An equation of the form y "+ ω 2 y \u003d 0 is called the equation of harmonic oscillations (mechanical, electrical, electromagnetic). The solution to such equations is the function

y = Asin(ωt + φ 0) or y = Acos(ωt + φ 0), where

A - oscillation amplitude, ω - cyclic frequency,

φ 0 - initial phase.

Lesson on the topic: "What is a derivative? Definition of a derivative"

Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions! All materials are checked by an antivirus program.

Teaching aids and simulators in the online store "Integral" for grade 10
Algebraic problems with parameters, grades 9–11
Software environment "1C: Mathematical constructor 6.1"

What will we study:
1. Introduction to the concept of a derivative.
2. A little bit of history.

4. Derivative on the graph of a function. The geometric meaning of the derivative.

6. Function differentiation.
7. Examples.

Introduction to the concept of derivative

There are many problems that are completely different in meaning, but at the same time there are mathematical models that allow us to calculate solutions to our problems in exactly the same way. For example, if we consider tasks such as:

A) There is some bank account that is constantly changing once every few days, the amount is constantly growing, you need to find how fast the account is growing.
b) The plant produces sweets, there is some constant increase in the production of sweets, find how quickly the increase in candies increases.
c) The speed of the car at some point in time t, if the position of the car is known, and it moves in a straight line.
d) We are given a graph of the function and at some point a tangent is drawn to it, we need to find the tangent of the slope to the tangent.
The wording of our problems is completely different, and it seems that they are solved in completely different ways, but mathematicians have figured out how to solve all these problems in exactly the same way. The concept of a derivative was introduced.

A little bit of history

The term derivative was introduced by the great mathematician - Lagrange, the translation into Russian is obtained from the French word derivee, he also introduced the modern notation for the derivative, which we will consider later.
Leibniz and Newton considered the concept of a derivative in their works, they found the application of our term in geometry and mechanics, respectively.
A little later, we will learn that the derivative is determined through the limit, but there is a small paradox in the history of mathematics. Mathematicians learned to calculate the derivative before they introduced the concept of a limit and actually understood what a derivative is.

Let the function y=f(x) be defined on some interval containing some point x0 inside. The increment of the argument Δx - does not go out of our interval. Let's find the increment Δy and compose the ratio Δy/Δx, if there is a limit of this ratio when Δx tends to zero, then the indicated limit is called the derivative of the function y=f(x) at the point x0 and is denoted by f'(x0).

Let's try to explain what a derivative is in a non-mathematical language:
In mathematical language: the derivative is the limit of the ratio of the increment of a function to the increment of its argument when the increment of the argument tends to zero.
In ordinary language: the derivative is the rate of change of the function at the point x0.
Let's look at the graphs of three functions:

Guys, what do you think, which of the curves grows faster?
The answer seems to be obvious to everyone 1 curve grows faster than the others. We look at how steeply the graph of the function goes up. In other words, how fast the ordinate changes as x changes. The same function at different points can have a different value of the derivative - that is, it can change faster or slower.

Derivative on the graph of a function. The geometric meaning of the derivative

Now let's see how to find the derivative using function graphs:


Let's look at our graph of the function: Let's draw a tangent to the graph of the function at the point c with abscissa x0. The tangent and the graph of our function are in contact at point A. We need to evaluate how steeply the graph of the function goes up. A convenient value for this is the tangent of the slope of the tangent.

Definition. The derivative of the function at the point x0 is equal to the tangent of the slope of the tangent drawn to the graph of the function at this point.

The slope angle of the tangent is chosen as the angle between the tangent and the positive direction of the x-axis.
And so the derivative of our function is equal to:

And so the derivative at the point x0 is equal to the tangent of the slope of the tangent, this is the geometric meaning of the derivative.

Algorithm for finding the derivative of the function y=f(x).
a) Fix the value x, find f(x).
b) Find the increment of the argument x+ Δx, and the value of the increment of the function f(x+ Δx).
c) Find the increment of the function Δy= f(x+ Δx)-f(x).
d) Compile the ratio: Δy / Δx
e) Calculate

This is the derivative of our function.

Function differentiation

If the function y=f(x) has a derivative at the point x, then it is called differentiable at the point x. The process of finding the derivative is called differentiation of the function y=f(x).
Let us return to the question of the continuity of a function. If the function is differentiable at some point, then a tangent can be drawn to the graph of the function at this point, the function cannot have a discontinuity at this point, then it is simply impossible to draw a tangent.
And so we write the above as a definition:
Definition. If a function is differentiable at a point x, then it is continuous at that point.
However, if a function is continuous at a point, then this does not mean that it is differentiable at that point. For example, the function y=|x| at the point x=0 is continuous, but the tangent cannot be drawn, and hence the derivative does not exist.

Derivative Examples

Find the derivative of a function: y=3x
Solution:
We will use the derivative search algorithm.
1) For a fixed value x, function value y=3x
2) At the point x+ Δx, y=f(x+ Δx)=3(x+ Δx)=3x+3 Δx

3) Find the increment of the function: Δy= f(x+ Δx)-f(x)= 3x+3 Δx-3x=3Δ

The derivative is the most important concept of mathematical analysis. It characterizes the change in the function of the argument x at some point. Moreover, the derivative itself is a function of the argument x

Derivative function at a point is called the limit (if it exists and is finite) of the ratio of the increment of the function to the increment of the argument, provided that the latter tends to zero.

The most common are the following derivative notation :

Example 1 Taking advantage definition of the derivative, find the derivative of the function

Solution. From the definition of the derivative follows the following scheme for its calculation.

Let's give the argument an increment (delta) and find the increment of the function:

Let's find the ratio of the increment of the function to the increment of the argument:

Let us calculate the limit of this ratio under the condition that the increment of the argument tends to zero, that is, the derivative required in the condition of the problem:

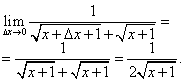
The physical meaning of the derivative

TO concept of derivative led Galileo Galilei's study of the law of free fall of bodies, and in a broader sense - the problem of the instantaneous velocity of non-uniform rectilinear motion of a point.

Let the pebble be lifted and then released from rest. Path s traversed in time t, is a function of time, that is. s = s(t). If the law of motion of a point is given, then it is possible to determine the average speed for any period of time. Let at the moment of time the pebble be in the position A, and at the moment - in the position B. Over a period of time (from t to ) the point has passed the path . Therefore, the average speed of movement for this period of time, which we denote by , is

.

However, the motion of a freely falling body is clearly uneven. Speed v the fall is constantly increasing. And the average speed is no longer enough to characterize the speed of movement on various sections of the path. This characteristic is the more accurate, the shorter the time interval. Therefore, the following concept is introduced: the instantaneous speed of rectilinear motion (or the speed at a given moment of time t) is called the average speed limit at:

(provided that this limit exists and is finite).

So it turns out that the instantaneous speed is the limit of the ratio of the increment of the function s(t) to the argument increment t at This is the derivative, which in general terms is written as follows:.

.

The solution of the designated problem is physical meaning of the derivative . So the derivative of the function y=f(x) at the point x the limit (if it exists and is finite) of the increment of the function to the increment of the argument is called, provided that the latter tends to zero.

Example 2 Find the derivative of a function

Solution. From the definition of the derivative follows the following scheme for its calculation.

Step 1. Let's increment the argument and find

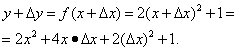
Step 2. Find the increment of the function:

Step 3. Find the ratio of the function increment to the argument increment:

Step 4. Calculate the limit of this ratio at , that is, the derivative:

The geometric meaning of the derivative

Let the function be defined on the interval and let the point M on the graph of the function corresponds to the value of the argument , and the point R- value . Pass through the dots M And R line and call it secant. Denote by the angle between the secant and the axis. Obviously, this angle depends on .

If exists

passing through the point is called the limit position of the secant MR at (or at ).

Tangent to the graph of a function at a point M called the limit position of the secant MR for , or, which is the same for .

It follows from the definition that for the existence of a tangent it is sufficient that there is a limit

,

moreover, the limit is equal to the angle of inclination of the tangent to the axis.

Now let's give a precise definition of a tangent.

Tangent to the graph of a function at a point is called a straight line passing through the point and having a slope, i.e. straight line whose equation

From this definition it follows that function derivative equal to the slope of the tangent to the graph of this function at the point with the abscissa x. This is the geometric meaning of the derivative.

In problem B9, a graph of a function or derivative is given, from which it is required to determine one of the following quantities:

1. The value of the derivative at some point x 0,
2. High or low points (extremum points),
3. Intervals of increasing and decreasing functions (intervals of monotonicity).

The functions and derivatives presented in this problem are always continuous, which greatly simplifies the solution. Despite the fact that the task belongs to the section of mathematical analysis, it is quite within the power of even the weakest students, since no deep theoretical knowledge is required here.

To find the value of the derivative, extremum points and monotonicity intervals, there are simple and universal algorithms - all of them will be discussed below.

Read the condition of problem B9 carefully so as not to make stupid mistakes: sometimes quite voluminous texts come across, but there are few important conditions that affect the course of the solution.

Calculation of the value of the derivative. Two point method

If the problem is given a graph of the function f(x), tangent to this graph at some point x 0 , and it is required to find the value of the derivative at this point, the following algorithm is applied:

1. Find two "adequate" points on the tangent graph: their coordinates must be integer. Let's denote these points as A (x 1 ; y 1) and B (x 2 ; y 2). Write down the coordinates correctly - this is the key point of the solution, and any mistake here leads to the wrong answer.
2. Knowing the coordinates, it is easy to calculate the increment of the argument Δx = x 2 − x 1 and the increment of the function Δy = y 2 − y 1 .
3. Finally, we find the value of the derivative D = Δy/Δx. In other words, you need to divide the function increment by the argument increment - and this will be the answer.

Once again, we note: points A and B must be sought precisely on the tangent, and not on the graph of the function f(x), as is often the case. The tangent will necessarily contain at least two such points, otherwise the problem is formulated incorrectly.

Consider the points A (−3; 2) and B (−1; 6) and find the increments:
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Let's find the value of the derivative: D = Δy/Δx = 4/2 = 2.

Task. The figure shows the graph of the function y \u003d f (x) and the tangent to it at the point with the abscissa x 0. Find the value of the derivative of the function f(x) at the point x 0 .

Consider points A (0; 3) and B (3; 0), find increments:
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

Now we find the value of the derivative: D = Δy/Δx = −3/3 = −1.

Task. The figure shows the graph of the function y \u003d f (x) and the tangent to it at the point with the abscissa x 0. Find the value of the derivative of the function f(x) at the point x 0 .

Consider points A (0; 2) and B (5; 2) and find increments:
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.

It remains to find the value of the derivative: D = Δy/Δx = 0/5 = 0.

From the last example, we can formulate the rule: if the tangent is parallel to the OX axis, the derivative of the function at the point of tangency is equal to zero. In this case, you don’t even need to calculate anything - just look at the graph.

Calculating High and Low Points

Sometimes instead of a graph of a function in problem B9, a derivative graph is given and it is required to find the maximum or minimum point of the function. In this scenario, the two-point method is useless, but there is another, even simpler algorithm. First, let's define the terminology:

1. The point x 0 is called the maximum point of the function f(x) if the following inequality holds in some neighborhood of this point: f(x 0) ≥ f(x).
2. The point x 0 is called the minimum point of the function f(x) if the following inequality holds in some neighborhood of this point: f(x 0) ≤ f(x).

In order to find the maximum and minimum points on the graph of the derivative, it is enough to perform the following steps:

1. Redraw the graph of the derivative, removing all unnecessary information. As practice shows, extra data only interfere with the decision. Therefore, we mark the zeros of the derivative on the coordinate axis - and that's it.
2. Find out the signs of the derivative on the intervals between zeros. If for some point x 0 it is known that f'(x 0) ≠ 0, then only two options are possible: f'(x 0) ≥ 0 or f'(x 0) ≤ 0. The sign of the derivative is easy to determine from the original drawing: if the derivative graph lies above the OX axis, then f'(x) ≥ 0. Conversely, if the derivative graph lies below the OX axis, then f'(x) ≤ 0.
3. We again check the zeros and signs of the derivative. Where the sign changes from minus to plus, there is a minimum point. Conversely, if the sign of the derivative changes from plus to minus, this is the maximum point. Counting is always done from left to right.

This scheme works only for continuous functions - there are no others in problem B9.

Task. The figure shows a graph of the derivative of the function f(x) defined on the segment [−5; 5]. Find the minimum point of the function f(x) on this segment.

Let's get rid of unnecessary information - we will leave only the borders [−5; 5] and the zeros of the derivative x = −3 and x = 2.5. Also note the signs:

Obviously, at the point x = −3, the sign of the derivative changes from minus to plus. This is the minimum point.

Task. The figure shows a graph of the derivative of the function f(x) defined on the segment [−3; 7]. Find the maximum point of the function f(x) on this segment.

Let's redraw the graph, leaving only the boundaries [−3; 7] and the zeros of the derivative x = −1.7 and x = 5. Note the signs of the derivative on the resulting graph. We have:

Obviously, at the point x = 5, the sign of the derivative changes from plus to minus - this is the maximum point.

Task. The figure shows a graph of the derivative of the function f(x) defined on the segment [−6; 4]. Find the number of maximum points of the function f(x) that belong to the interval [−4; 3].

It follows from the conditions of the problem that it is sufficient to consider only the part of the graph bounded by the segment [−4; 3]. Therefore, we build a new graph, on which we mark only the boundaries [−4; 3] and the zeros of the derivative inside it. Namely, the points x = −3.5 and x = 2. We get:

On this graph, there is only one maximum point x = 2. It is in it that the sign of the derivative changes from plus to minus.

A small note about points with non-integer coordinates. For example, in the last problem, the point x = −3.5 was considered, but with the same success we can take x = −3.4. If the problem is formulated correctly, such changes should not affect the answer, since the points "without a fixed place of residence" are not directly involved in solving the problem. Of course, with integer points such a trick will not work.

Finding intervals of increase and decrease of a function

In such a problem, like the points of maximum and minimum, it is proposed to find areas in which the function itself increases or decreases from the graph of the derivative. First, let's define what ascending and descending are:

1. A function f(x) is called increasing on a segment if for any two points x 1 and x 2 from this segment the statement is true: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). In other words, the larger the value of the argument, the larger the value of the function.
2. A function f(x) is called decreasing on a segment if for any two points x 1 and x 2 from this segment the statement is true: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Those. a larger value of the argument corresponds to a smaller value of the function.

We formulate sufficient conditions for increasing and decreasing:

1. For a continuous function f(x) to increase on the segment , it is sufficient that its derivative inside the segment be positive, i.e. f'(x) ≥ 0.
2. For a continuous function f(x) to decrease on the segment , it is sufficient that its derivative inside the segment be negative, i.e. f'(x) ≤ 0.

We accept these assertions without proof. Thus, we obtain a scheme for finding intervals of increase and decrease, which is in many ways similar to the algorithm for calculating extremum points:

1. Remove all redundant information. On the original graph of the derivative, we are primarily interested in the zeros of the function, so we leave only them.
2. Mark the signs of the derivative at the intervals between zeros. Where f'(x) ≥ 0, the function increases, and where f'(x) ≤ 0, it decreases. If the problem has restrictions on the variable x, we additionally mark them on the new chart.
3. Now that we know the behavior of the function and the constraint, it remains to calculate the required value in the problem.

Task. The figure shows a graph of the derivative of the function f(x) defined on the segment [−3; 7.5]. Find the intervals of decreasing function f(x). In your answer, write the sum of integers included in these intervals.

As usual, we redraw the graph and mark the boundaries [−3; 7.5], as well as the zeros of the derivative x = −1.5 and x = 5.3. Then we mark the signs of the derivative. We have:

Since the derivative is negative on the interval (− 1.5), this is the interval of decreasing function. It remains to sum all the integers that are inside this interval:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Task. The figure shows a graph of the derivative of the function f(x) defined on the segment [−10; 4]. Find the intervals of increasing function f(x). In your answer, write the length of the largest of them.

Let's get rid of redundant information. We leave only the boundaries [−10; 4] and zeros of the derivative, which this time turned out to be four: x = −8, x = −6, x = −3 and x = 2. Note the signs of the derivative and get the following picture:

We are interested in the intervals of increasing function, i.e. where f'(x) ≥ 0. There are two such intervals on the graph: (−8; −6) and (−3; 2). Let's calculate their lengths:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Since it is required to find the length of the largest of the intervals, we write the value l 2 = 5 in response.