Vektorový súčin matice. Ako nájsť krížový súčin vektorov

Bodové vlastnosti produktu

Bodový súčin vektorov, definícia, vlastnosti

Lineárne operácie s vektormi.

Vektory, základné pojmy, definície, lineárne operácie s nimi

Vektor v rovine je usporiadaná dvojica jeho bodov, pričom prvý bod sa nazýva začiatok a druhý koniec - vektora.

Dva vektory sa nazývajú rovnaké, ak sú rovnaké a kosmerné.

Vektory, ktoré ležia na tej istej priamke, sa nazývajú kosmerné, ak sú kosmerné s niektorým z toho istého vektora, ktorý neleží na tejto priamke.

Vektory, ktoré ležia na rovnakej priamke alebo na rovnobežných priamkach, sa nazývajú kolineárne a kolineárne, ale nie kosmerné, sa nazývajú opačne orientované.

Vektory ležiace na kolmých čiarach sa nazývajú ortogonálne.

Definícia 5.4. súčet a+b vektory a a b sa nazýva vektor pochádzajúci zo začiatku vektora a na koniec vektora b , ak je začiatok vektora b sa zhoduje s koncom vektora a .

Definícia 5.5. rozdiel a - b vektory a a b takýto vektor sa nazýva s , ktorý spolu s vektorom b dáva vektor a .

Definícia 5.6. prácak a vektor a za číslo k nazývaný vektor b , kolineárny vektor a , ktorý má modul rovný | k||a |, a smer, ktorý je rovnaký ako smer a pri k>0 a naopak a pri k<0.

Vlastnosti násobenia vektora číslom:

Nehnuteľnosť 1. k(a+b ) = k a+ k b.

Nehnuteľnosť 2. (k+m)a = k a+ m a.

Nehnuteľnosť 3. k(m a) = (km)a .

Dôsledok. Ak nenulové vektory a a b sú kolineárne, potom je tu číslo k, čo b= k a.

Skalárny súčin dvoch nenulových vektorov a a b nazývané číslo (skalár), ktoré sa rovná súčinu dĺžok týchto vektorov a kosínusu uhla φ medzi nimi. Skalárny súčin môže byť vyjadrený rôznymi spôsobmi, napríklad ako ab, a · b, (a , b), (a · b). Takže bodkový produkt je:

a · b = |a| · | b| cos φ

Ak sa aspoň jeden z vektorov rovná nule, potom sa skalárny súčin rovná nule.

Permutačná vlastnosť: a · b = b · a(skalárny súčin sa nemení permutáciou faktorov);

distribučná vlastnosť: a · ( b · c) = (a · b) · c(výsledok nezávisí od poradia násobenia);

Kombinačná vlastnosť (vo vzťahu ku skalárnemu faktoru): (λ a) · b = λ ( a · b).

Vlastnosť ortogonality (kolmosti): ak vektor a a b nenulové, ich bodový súčin je nulový iba vtedy, keď sú tieto vektory ortogonálne (na seba kolmé) a ┴ b;

Štvorcová vlastnosť: a · a = a 2 = |a| 2 (skalárny súčin vektora so sebou samým sa rovná druhej mocnine jeho modulu);

Ak súradnice vektorov a=(x1, y1, z1) a b=(x2, y2, z2), potom je skalárny súčin a · b= x 1 x 2 + y1y2 + z1z2.

Vektorové držiace vektory. Definícia: Vektorový súčin dvoch vektorov a chápe sa ako vektor, pre ktorý:

Modul sa rovná ploche rovnobežníka postaveného na týchto vektoroch, t.j. , kde je uhol medzi vektormi a

Tento vektor je kolmý na násobené vektory, t.j.

Ak sú vektory nekolineárne, potom tvoria pravú trojicu vektorov.

Vlastnosti krížových produktov:

1. Pri zmene poradia faktorov vektorový súčin zmení svoje znamienko na opačné, pričom modul zachová, t.j.

2 .Vektorový štvorec sa rovná nule-vektor, t.j.

3 .Skalárny faktor možno vyňať zo znamienka vektorového súčinu, t.j.

4 .Pre ľubovoľné tri vektory je rovnosť

5 Nevyhnutná a postačujúca podmienka pre kolinearitu dvoch vektorov a :

Táto online kalkulačka počíta krížový súčin vektorov. Uvádza sa podrobné riešenie. Ak chcete vypočítať krížový súčin vektorov, zadajte súradnice vektorov do buniek a kliknite na tlačidlo "Vypočítať."

×

POZOR

Vymazať všetky bunky?

Zavrieť Vymazať

Návod na zadávanie údajov.Čísla sa zadávajú ako celé čísla (príklady: 487, 5, -7623 atď.), desatinné čísla (napr. 67., 102,54 atď.) alebo zlomky. Zlomok musí byť napísaný v tvare a/b, kde a a b (b>0) sú celé čísla alebo desatinné čísla. Príklady 45/5, 6,6/76,4, -7/6,7 atď.

Krížový súčin vektorov

Predtým, ako pristúpite k definícii vektorového súčinu vektorov, zvážte koncepty usporiadaná trojica vektorov, ľavá trojica vektorov, pravá trojica vektorov.

Definícia 1. Volajú sa tri vektory objednaný trojitý(alebo trojitý), ak je uvedené, ktorý z týchto vektorov je prvý, ktorý je druhý a ktorý je tretí.

Nahrávanie cba- znamená - prvý je vektor c, druhý je vektor b a tretí je vektor a.

Definícia 2. Trojica nekoplanárnych vektorov abc nazývaný pravý (ľavý), ak sú tieto vektory po zmenšení na spoločný začiatok usporiadané tak, že sú umiestnené veľké, neohnuté ukazováky a prostredníky pravej (ľavej) ruky.

Definícia 2 môže byť formulovaná aj inak.

Definícia 2. Trojica nekoplanárnych vektorov abc sa nazýva pravý (ľavý), ak sa pri redukovaní na spoločný pôvod vektor c umiestnené na druhej strane roviny definovanej vektormi a a b, odkiaľ je najkratšia odbočka a do b vykonávané proti smeru hodinových ručičiek (v smere hodinových ručičiek).

Vektorové trio abc znázornené na obr. 1 je pravý a trojitý abc znázornené na obr. 2 zostáva.

Ak sú dve trojice vektorov vpravo alebo vľavo, potom sa hovorí, že majú rovnakú orientáciu. Inak sú vraj opačne orientovaní.

Definícia 3. Kartézsky alebo afinný súradnicový systém sa nazýva pravý (ľavý), ak tri základné vektory tvoria pravú (ľavú) trojicu.

Pre istotu, v nasledujúcom budeme uvažovať iba o pravotočivých súradnicových systémoch.

Definícia 4. vektorové umenie vektor a na vektor b nazývaný vektor s, označené symbolom c=[ab] (alebo c=[a,b], príp c=a×b) a spĺňa tieto tri požiadavky:

• vektorová dĺžka s sa rovná súčinu dĺžok vektorov a a b na sínus uhla φ medzi nimi:

|c|=|[ab]|=|a||b|sinφ;

(1)

• vektor s ortogonálne ku každému z vektorov a a b;
• vektor c nasmerovaný tak, že tri abc je správne.

Krížový súčin vektorov má tieto vlastnosti:

• [ab]=−[ba] (antipermutabilita faktory);
• [(λa)b]=λ [ab] (kompatibilita vo vzťahu k číselnému faktoru);
• [(a+b)c]=[ac]+[bc] (distribúcia relatívne k súčtu vektorov);
• [aa]=0 pre ľubovoľný vektor a.

Geometrické vlastnosti krížového súčinu vektorov

Veta 1. Aby boli dva vektory kolineárne, je potrebné a postačujúce, aby ich vektorový súčin bol rovný nule.

Dôkaz. Potreba. Nechajte vektory a a b kolineárne. Potom je uhol medzi nimi 0 alebo 180° a sinφ=hriech180=hriech 0 = 0. Preto, berúc do úvahy výraz (1), dĺžku vektora c rovná sa nule. Potom c nulový vektor.

Primeranosť. Nechajte krížový súčin vektorov a a b navigácia na nulu: [ ab]=0. Dokážme, že vektory a a b kolineárne. Ak aspoň jeden z vektorov a a b nula, potom sú tieto vektory kolineárne (pretože nulový vektor má neurčitý smer a možno ho považovať za kolineárny s ľubovoľným vektorom).

Ak oba vektory a a b nenulová, potom | a|>0, |b|>0. Potom od [ ab]=0 a z (1) to vyplýva sinφ=0. Preto tie vektory a a b kolineárne.

Veta bola dokázaná.

Veta 2. Dĺžka (modul) vektorového súčinu [ ab] sa rovná ploche S rovnobežník postavený na vektoroch zredukovaných na spoločný pôvod a a b.

Dôkaz. Ako viete, plocha rovnobežníka sa rovná súčinu susedných strán tohto rovnobežníka a sínusu uhla medzi nimi. V dôsledku toho:

Potom má krížový súčin týchto vektorov tvar:

Rozšírením determinantu o prvky prvého riadku dostaneme rozklad vektora a×b základ i, j, k, čo je ekvivalentné so vzorcom (3).

Dôkaz vety 3. Zostavte všetky možné dvojice bázových vektorov i, j, k a vypočítať ich vektorový súčin. Je potrebné vziať do úvahy, že základné vektory sú navzájom ortogonálne, tvoria pravú trojicu a majú jednotkovú dĺžku (inými slovami, môžeme predpokladať, že i={1, 0, 0}, j={0, 1, 0}, k=(0, 0, 1)). Potom máme:

Z poslednej rovnosti a vzťahov (4) dostaneme:

Zostavte maticu 3×3, ktorej prvý riadok sú základné vektory i, j, k, a zvyšné riadky sú vyplnené prvkami vektorov a a b:

Teda výsledok krížového súčinu vektorov a a b bude vektor:

.

Príklad 2. Nájdite krížový súčin vektorov [ ab], kde je vektor a reprezentované dvoma bodkami. Počiatočný bod vektora a: , koncový bod vektora a: , vektor b má formu .

Riešenie: Presuňte prvý vektor do počiatku. Za týmto účelom odpočítajte od príslušných súradníc koncového bodu súradnice začiatočného bodu:

Determinant tejto matice vypočítame tak, že ju rozvinieme v prvom riadku. Výsledkom týchto výpočtov získame vektorový súčin vektorov a a b.

Definícia. Vektorový súčin vektora a a vektora b je vektor označený symbolom [«, b] (alebo l x b), takže 1) dĺžka vektora [a, b] je rovná (p, kde y je uhol medzi vektormi a a b ( 31), 2) vektor [a, b) je kolmý na vektory a a b, t.j. kolmá na rovinu týchto vektorov; 3) vektor [a, b] je nasmerovaný tak, že od konca tohto vektora je vidieť najkratší obrat z a do b proti smeru hodinových ručičiek (obr. 32). Ryža. 32 Obr.31 Inými slovami, vektory a, b a [а, b) tvoria pravú trojicu vektorov, t.j. umiestnené ako palec, ukazovák a prostredník pravej ruky. Ak sú vektory a a b kolineárne, budeme predpokladať, že [a, b] = 0. Podľa definície sa dĺžka vektorového súčinu numericky rovná ploche Sa rovnobežníka (obr. 33) postaveného na vynásobených vektoroch. a a b ako na stranách: 6.1 . Vlastnosti vektorového súčinu 1. Vektorový súčin sa rovná nulovému vektoru vtedy a len vtedy, ak je aspoň jeden z vynásobených vektorov nula alebo keď sú tieto vektory kolineárne (ak sú vektory a a b kolineárne, potom uhol medzi nimi je buď 0 alebo 7r). To sa dá ľahko získať z faktu, že Ak uvažujeme nulový vektor kolinzar k ľubovoľnému vektoru, potom podmienku kolinarity vektorov a a b možno vyjadriť nasledovne 2. Vektorový súčin je antikomutatívny, t.j. vždy. V skutočnosti vektory (a, b) a majú rovnakú dĺžku a sú kolineárne. Smery týchto vektorov sú opačné, pretože od konca vektora [a, b] bude vidieť najkratší obrat z a do b proti smeru hodinových ručičiek a od konca vektora [b, a] - v smere hodinových ručičiek (obr. 34). 3. Vektorový súčin má distribučnú vlastnosť vzhľadom na sčítanie 4. Číselný faktor A možno vyňať zo znamienka vektorového súčinu 6.2. Vektorový súčin vektorov daný súradnicami Nech sú vektory a a b dané súradnicami v základe. Pomocou distribučnej vlastnosti vektorového súčinu nájdeme vektorový súčin vektorov daný súradnicami. Zmiešaná práca. Vypíšme vektorové súčiny súradnicových ortov (obr. 35): Preto pre vektorový súčin vektorov a a b získame zo vzorca (3) nasledujúci výrazový determinant nad prvkami 1. riadku, dostaneme ( 4). Príklady. 1. Nájdite oblasť rovnobežníka postaveného na vektoroch Nájdite oblasť trojuholníka (obr. 36). Je zrejmé, že plocha b "d trojuholníka JSC sa rovná polovici plochy S rovnobežníka O AC B. Výpočet vektorového súčinu (a, b | vektorov a \u003d OA a b \u003d b \u003d ob ), dostaneme (a, b), c) = [a, |b, c)) vo všeobecnom prípade neplatí Napríklad pre a = ss j máme § 7. Zmiešaný súčin vektorov Nech máme tri vektory a, b a c. Vektorovo vynásobíme vektory a a 1>. Výsledkom je vektor [a, 1>], ktorý skalárne vynásobíme vektorom c: (k b), c. Číslo ( [a, b], e) sa nazýva zmiešaný súčin vektorov a, b) c a označuje sa symbolom (a, 1), e) 7.1 Geometrický význam zmiešaného súčinu Ponechajme stranou vektory a, b a zo všeobecného bodu O (obr. 37) Ak všetky štyri body O, A, B, C ležia v rovnakej rovine (vektory a, b a c sa v tomto prípade nazývajú koplanárne), potom zmiešané súčin ([a, b], c) = 0. Vyplýva to z toho, že vektor [a, b| je kolmý na rovinu, v ktorej ležia vektory a a 1 ", a teda vektor c. / Ak t body O, A, B, C neležia v rovnakej rovine (vektory a, b a c sú nekoplanárne), na hranách OA, OB a OS postavíme rovnobežnosten (obr. 38 a). Podľa definície krížového súčinu máme (a,b) = So c, kde So je plocha rovnobežníka OADB a c je jednotkový vektor kolmý na vektory a a b a taký, že trojité a , b, c je správne, t.j. vektory a, b a c sú umiestnené ako palec, ukazovák a prostredník pravej ruky (obr. 38 b). Vynásobením oboch častí poslednej rovnosti na pravom skaláre vektorom c dostaneme, že vektorový súčin vektorov daný súradnicami. Zmiešaná práca. Číslo rc c sa rovná výške h zostrojeného kvádra, pričom sa berie so znamienkom „+“, ak je uhol medzi vektormi c a c ostrý (trojica a, b, c je pravá), a so znamienkom „ -“ ak je uhol tupý (trojité a, b, c - vľavo), takže zmiešaný súčin vektorov a, b a c sa rovná objemu V kvádra postaveného na týchto vektoroch ako na hranách ak je trojica a, b, c vpravo a -V, ak je trojica a, b, c - vľavo. Na základe geometrického významu zmiešaného súčinu môžeme usúdiť, že vynásobením rovnakých vektorov a, b a c v akomkoľvek inom poradí vždy dostaneme buď +7 alebo -K. Znak pro- Obr. 38 odkaz bude závisieť len od toho, ktorý triplet tvoria vynásobené vektory - pravý alebo ľavý. Ak vektory a, b, c tvoria pravú trojicu, potom trojice b, c, a a c, a, b budú tiež pravé. Súčasne všetky tri triplety b, a, c; a, c, b a c, b, a - vľavo. Teda (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b , a). Ešte raz zdôrazňujeme, že zmiešaný súčin vektorov sa rovná nule práve vtedy, ak sú vynásobené vektory a, b, c koplanárne: (a, b, c sú koplanárne) 7.2. Zmiešaný súčin v súradniciach Nech sú vektory a, b, c dané súradnicami v báze i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Nájdime výraz pre ich zmiešaný súčin (a, b, c). Máme zmiešaný súčin vektorov daný ich súradnicami v báze i, J, k rovný determinantu tretieho rádu, ktorého čiary sú zložené zo súradníc prvého, druhého a tretieho vynásobeného vektory. Nevyhnutnú a postačujúcu podmienku komplanárnosti vektorov a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) je možné zapísať v nasledujúcom tvare z, ar2y2-2 = 0. Príklad Uz. Skontrolujte, či vektory v = (7,4,6), b = (2, 1,1), c = (19, II, 17) sú koplanárne. Uvažované vektory budú koplanárne alebo nekoplanárne v závislosti od toho, či sa determinant rovná nule alebo nie. Rozšírením o prvky prvého riadku dostaneme 7.3. Dvojitý krížový súčin Dvojitý krížový súčin [a, [b, c]] je vektor kolmý na vektory a a [b, c]. Preto leží v rovine vektorov b a c a môže sa v týchto vektoroch rozširovať. Dá sa ukázať, že platí vzorec [a, [!>, c]] = b(a, e) - c(a, b). Cvičenia 1. Tri vektory AB = c, W? = o a CA = b slúžia ako strany trojuholníka. Vyjadrite pomocou a, b a c vektory, ktoré sa zhodujú s mediánmi AM, DN, CP trojuholníka. 2. Aká podmienka musí byť spojená medzi vektormi p a q, aby vektor p + q rozdelil uhol medzi nimi na polovicu? Predpokladá sa, že všetky tri vektory súvisia so spoločným pôvodom. 3. Vypočítajte dĺžku uhlopriečok rovnobežníka postaveného na vektoroch a = 5p + 2q a b = p - 3q, ak je známe, že |p| = 2v/2, |q| = 3H-(p7ci) = f. 4. Označením strán kosoštvorca aab strany kosoštvorca vychádzajúceho zo spoločného vrcholu dokážte, že uhlopriečky kosoštvorca sú navzájom kolmé. 5. Vypočítajte bodový súčin vektorov a = 4i + 7j + 3k a b = 31 - 5j + k. 6. Nájdite jednotkový vektor a0 rovnobežný s vektorom a = (6, 7, -6). 7. Nájdite priemet vektora a = l+ j- kHa vektor b = 21 - j - 3k. 8. Nájdite kosínus uhla medzi vektormi IS "w, ak A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Nájdite jednotkový vektor p°, ktorý je súčasne kolmý na vektor a = (3, 6, 8) a os x. 10. Vypočítajte sínus uhla medzi uhlopriečkami rovnobežníka postaveného na vektoroch a = 2i+J-k, b=i-3j + k ako na stranách. Vypočítajte výšku h kvádra postaveného na vektoroch a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k, ak sa za základ vezme rovnobežník zostavený z vektorov a a I). Odpovede

Je zrejmé, že v prípade krížového produktu záleží na poradí, v ktorom sú vektory prijaté, navyše,

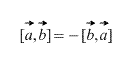
Priamo z definície tiež vyplýva, že pre akýkoľvek skalárny faktor k (číslo) platí:

Krížový súčin kolineárnych vektorov sa rovná nulovému vektoru. Krížový súčin dvoch vektorov je navyše nulový vtedy a len vtedy, ak sú kolineárne. (V prípade, že jeden z nich je nulový vektor, je potrebné pamätať na to, že nulový vektor je podľa definície kolineárny s ľubovoľným vektorom).

Vektorový produkt má distribučný majetok, teda

Vyjadrenie krížového produktu v zmysle súradníc vektorov.

Nech sú dané dva vektory

(ako zistiť súradnice vektora podľa súradníc jeho začiatku a konca - pozri článok Bodový súčin vektorov, odsek Alternatívna definícia bodového súčinu, alebo výpočet bodového súčinu dvoch vektorov daných ich súradnicami.)

Prečo potrebujete vektorový produkt?

Existuje mnoho spôsobov, ako použiť krížový súčin, napríklad, ako už bolo napísané vyššie, výpočtom krížového súčinu dvoch vektorov môžete zistiť, či sú kolineárne.

Alebo sa dá použiť ako spôsob výpočtu plochy rovnobežníka vytvoreného z týchto vektorov. Na základe definície je dĺžka výsledného vektora oblasťou tohto rovnobežníka.

Online kalkulačka vektorového produktu.

Ak chcete pomocou tejto kalkulačky nájsť skalárny súčin dvoch vektorov, musíte zadať súradnice prvého vektora do prvého riadku v poradí a druhého vektora do druhého. Súradnice vektorov možno vypočítať z ich počiatočných a koncových súradníc (pozri článok Bodový súčin vektorov , položka Alternatívna definícia bodového súčinu alebo výpočet bodového súčinu dvoch vektorov vzhľadom na ich súradnice.)

Definícia. Vektorový súčin vektora a (násobiteľa) vektorom (násobiteľom), ktorý s ním nie je kolineárny, je tretí vektor c (súčin), ktorý je skonštruovaný takto:

1) jeho modul sa číselne rovná ploche rovnobežníka na obr. 155), postavený na vektoroch, t.j. rovná sa smeru kolmému na rovinu uvedeného rovnobežníka;

3) smer vektora c sa v tomto prípade volí (z dvoch možných) tak, aby vektory c tvorili pravotočivú sústavu (§ 110).

Označenie: alebo

Dodatok k definícii. Ak sú vektory kolineárne, potom vzhľadom na obrázok ako (podmienečne) rovnobežník je prirodzené priradiť nulovú plochu. Preto sa vektorový súčin kolineárnych vektorov považuje za rovný nulovému vektoru.

Keďže nulovému vektoru možno priradiť akýkoľvek smer, táto konvencia nie je v rozpore s bodmi 2 a 3 definície.

Poznámka 1. Vo výraze "vektorový súčin" prvé slovo označuje, že výsledkom činnosti je vektor (na rozdiel od skalárneho súčinu; porovnaj § 104, poznámka 1).

Príklad 1. Nájdite vektorový súčin, kde sú hlavné vektory pravého súradnicového systému (obr. 156).

1. Keďže dĺžky hlavných vektorov sa rovnajú jednotke mierky, plocha rovnobežníka (štvorca) sa číselne rovná jednej. Preto je modul vektorového produktu rovný jednej.

2. Keďže kolmica na rovinu je osou, požadovaný vektorový súčin je vektor kolineárny s vektorom k; a keďže obidve majú modul 1, požadovaný krížový súčin je buď k alebo -k.

3. Z týchto dvoch možných vektorov treba vybrať prvý, keďže vektory k tvoria pravý systém (a vektory tvoria ľavý).

Príklad 2. Nájdite krížový súčin

Riešenie. Ako v príklade 1 sme dospeli k záveru, že vektor je buď k alebo -k. Teraz však musíme zvoliť -k, pretože vektory tvoria pravý systém (a vektory tvoria ľavý). takže,

Príklad 3 Vektory majú dĺžku 80 a 50 cm a zvierajú uhol 30°. Ak vezmeme meter ako jednotku dĺžky, nájdite dĺžku vektorového súčinu a

Riešenie. Plocha rovnobežníka postaveného na vektoroch sa rovná Dĺžka požadovaného vektorového produktu sa rovná

Príklad 4. Nájdite dĺžku krížového súčinu tých istých vektorov, pričom ako jednotku dĺžky vezmite centimeter.

Riešenie. Keďže plocha rovnobežníka postaveného na vektoroch sa rovná dĺžke vektorového súčinu je 2000 cm, t.j.

Porovnanie príkladov 3 a 4 ukazuje, že dĺžka vektora závisí nielen od dĺžok faktorov, ale aj od voľby dĺžkovej jednotky.

Fyzikálny význam vektorového produktu. Z mnohých fyzikálnych veličín reprezentovaných vektorovým súčinom budeme uvažovať iba moment sily.

Nech je bod pôsobenia sily A. Moment sily vzhľadom na bod O sa nazýva vektorový súčin. Keďže modul tohto vektorového súčinu sa numericky rovná ploche rovnobežníka (obr. 157), modul momentu sa rovná súčinu základne výškou, t.j. sila vynásobená vzdialenosťou od bodu O k priamke, pozdĺž ktorej sila pôsobí.

V mechanike je dokázané, že pre rovnováhu tuhého telesa je potrebné, aby nielen súčet vektorov reprezentujúcich sily pôsobiace na teleso, ale aj súčet momentov síl bol rovný nule. V prípade, že sú všetky sily rovnobežné s tou istou rovinou, sčítanie vektorov reprezentujúcich momenty môže byť nahradené sčítaním a odčítaním ich modulov. Ale pre svojvoľné smery síl je takáto náhrada nemožná. V súlade s tým je krížový súčin definovaný presne ako vektor a nie ako číslo.